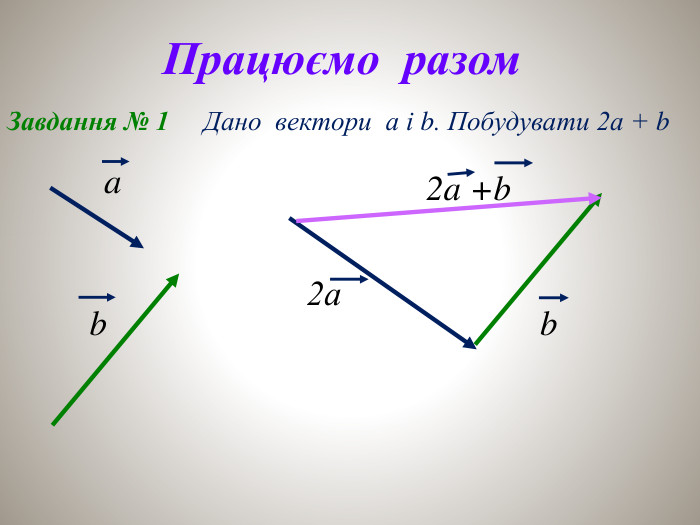
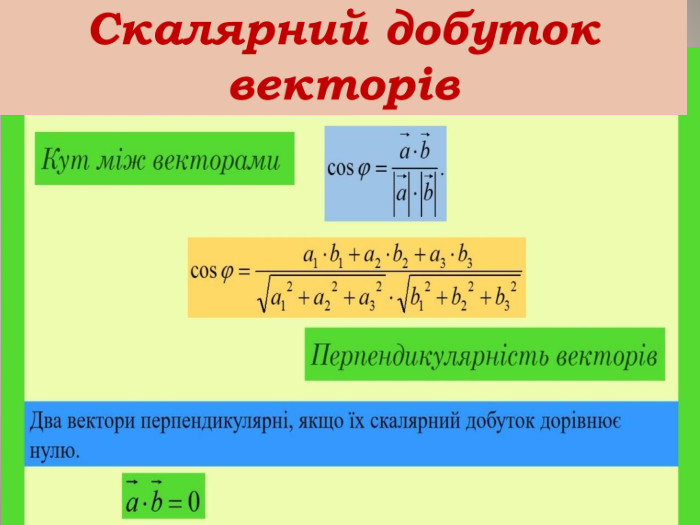
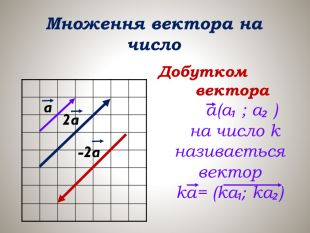
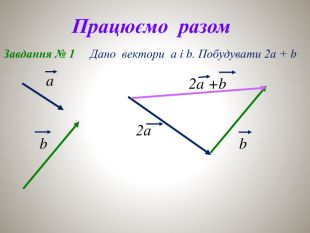
Презентаціця "Множення векторів"
Про матеріал
Презентація "Множення векторів" допоможе вчителю в доступній формі і на простих прикладах подати і закріпити навчальний матеріал з теми Перегляд файлу
Зміст слайдів
pptx
До підручника
Геометрія 9 клас (Єршова А. П., Голобородько В.В., Крижановський О.Ф., Єршов С. В.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку