Практична робота. «Розрахунок площі бічної та повної поверхні циліндра».
Практична робота
Тема. «Розрахунок площі бічної та повної поверхні циліндра».
Мета роботи: навчитися розраховувати площі бічної та повної поверхні циліндра, площі осьового перерізу циліндра.
Прилади та матеріали: модель циліндра, лінійка, циркуль, олівець.
Хід роботи:
|
I. Виконайте наступні вимірювання |
|
|
|
1) Вимірюємо радіус циліндра r =
2) Вимірюємо довжину твірної (висоти) циліндра h =
3) Підписати знайдені розміри (висоту та радіус) на рисунку 1. |
|
II. Знайти площу бічної поверхні циліндра: |
|
|
рис.2 Площа бічної поверхні циліндра дорівнює площі розгортки
|
1) Знайдемо довжину кола основи циліндра за формулою: C = 2π r ; C = 2) Підписати на рисунку 2 значення висоти циліндра та довжини кола.
3) Знайдемо площу бічної поверхні циліндра за формулою: Sбіч.= Sбіч.= |
|
III. Знайти площу основи циліндра: |
|
|
рис.3
Основа циліндра - коло радіусу r. |
Sосн. = ; Sосн. =
|
|
IV. Знайти площу повної поверхні циліндра: |
|
|
рис.4
|
1) Підписати на рисунку 4, бічну поверхню та основи.
2) Знайдемо площу повної поверхні циліндра за формулою:
Sпов= Sбок+2Sосн Sпов= |
|
V. Знайти площу осьового перерізу циліндра: |
|
|
Осьовий переріз циліндра є прямокутник, дві сторони якого – дорівнюють висоті циліндра h, а дві інші – діаметри основ циліндра d або 2r.
|
1) Підписати розміри висоти та радіусу на рисунку 5.
2) Знайдемо площу осьового перерізу циліндра за формулою:
Sос.пер.= 2rh; Sос.пер.=
|
Висновок: під час виконання роботи я навчився розраховувати площі бічної, повної поверхні та осьового перерізу циліндра.


про публікацію авторської розробки
Додати розробку

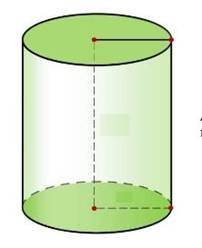 рис.1
рис.1
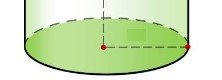
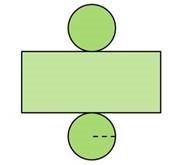
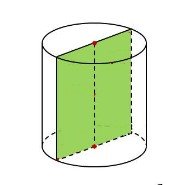 рис.5
рис.5