Практичне заняття "Різні типи задач на координати та вектори"

СИСТЕМИ ЗАДАЧ, ПРИЗНАЧЕНІ ДЛЯ НАВЧАННЯ УЧНІВ РОЗВ’ЯЗУВАННЯ РІЗНИХ ТИПІВ ЗАДАЧ НА КООРДИНАТИ ТА ВЕКТОРИ

      1.1. Задачі на використання відомостей про координати

Розглянемо задачу, яку можна розв’язати двома способами, використовуючи відомості про координати.

 Задача 1. Вершини чотирикутника мають координати , , , . Доведіть, що паралелограм.

Розв’язання. 1-й спосіб. Як відомо, за ознакою паралелограми чотирикутник, діагоналі якого точкою перетину діляться навпіл, є паралелограмом. Знайдемо координати середин діагоналей і . Середина відрізка має координати . Середина відрізка має координати . Отже, відрізки і мають спільну середину , тобто чотирикутник паралелограм за ознакою.

2-й спосіб. Як відомо, за ознакою паралелограма чотирикутник, протилежні сторони якого попарно рівні, є паралелограмом. Знайдемо довжини сторін чотирикутника :

, ;

, .

Отже, , , тобто чотирикутник паралелограм за ознакою.

Задача 2. Визначте центр і радіус кола, заданого рівнянням .

Розв’язання. Зведемо дане рівняння до вигляду . Маємо .

Додамо до обох частин цієї рівності числа так, щоб виділити квадрати двочленів і : ,        . Отже, дане коло має радіус 4 і центр

Задача 3. Складіть рівняння прямої, яка проходить через точки і .

Розв’язання. Оскільки абсциси точок і не рівні, пряма не паралельна осі ординат. Отже, будемо шукати її рівняння у вигляді . За умовою задачі координати точок і задовольняють шукане рівняння, тобто

Розв’язком системи цих рівнянь буде пара . Таким чином, шукане рівняння буде .

Зведемо його до вигляду : ; .

 

      1.2. Задачі на використання відомостей про вектори

Задача 4. Знайдіть координати четвертої вершини паралелограма , якщо

Розв’язання. Якщо чотирикутник – паралелограм, то . Нехай шукана вершина . Знайдемо координати векторів і :

;.

Отже, , , звідки .

Відповідь.

Задача 5. Дано вектори . Знайти координати вектора , такого, що .

Розв’язання. В цій задачі скористаємося означенням суми векторів через координати, а також означення рівних векторів. Тобто координати вектора, що є сумою векторів і такі ж, як і координати вектора . Використаємо це. Нехай маємо вектор . Тоді: .

Звідки

Відповідь. .

Задача 6. Доведіть, що точки лежать на одній прямій.

Розв’язування. Визначимо координати векторів і : , . Зауважимо, що , тобто . Це означає, що вектори і колінеарні, тобто мають лежати на одній прямій або на паралельних прямих. Але прямі і мають спільну точку , тобто точки і лежать на одній прямій.

Задача 7. При якому значенні вектори і перпендикулярні?

Розв’язання. Вектори і перпендикулярні за умови . Записавши цю умову в координатах, маємо: , , .

Відповідь. При .

      1.3. Застосування координатного, векторного та векторно-координатного методу до розв’язування задач

Задача 8. Знайти координати  середини відрізка , якщо , .

Розв’язання. Якщо точка – середина відрізка , то , . Отже, .

Відповідь.

Задача 9. Дано:

      Довести .

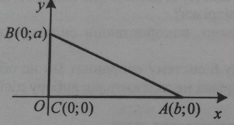Уведемо систему координат так, щоб катети і лежали на осях і відповідно, а точка – у початку координат. У цій системі координат вершини трикутника матимуть координати: , , Знайдемо довжину відрізка , а за умовою . Отже,

 Задача 10. Точка перетину відрізків, що сполучають середини протилежних сторін чотирикутника, збігається з точкою перетину його діагоналей. Доведіть, що даний чотирикутник – паралелограм.

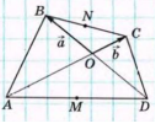 Розв’язання. Нехай діагоналі чотирикутника перетинаються в точці , точки і – середини сторін і відповідно. Позначимо , . Тоді . Оскільки , то , , отже, , де і – деякі числа.

За умовою задачі вектори і колінеарні, отже, , або . Звідси . Але оскільки вектори і неколінеарні, рівність можлива лише за умови . Отже, , , тобто вектори і колінеарні, звідки . Аналогічно можна довести, що . Таким чином, паралелограм.

 Для розв’язування задач векторно-координатним методом можна запропонувати наступну схему:

1. робимо рисунок до задачі;
2. вибираємо базисні (основні) вектори;
3. виражаємо дані вектори через базисні;
4. виконуємо операції над знайденими векторними залежностями за правилами векторної алгебри;
5. інтерпретуємо результативну векторну рівність на мові геометрії;
6. Записуємо відповідь за задачі.

Задачі, що розв’язуються векторно-координатним методом, поділяються на три типи: задачі на доведення; задачі на обчислення; задачі на побудову. Розглянемо приклади розв’язування таких задач.

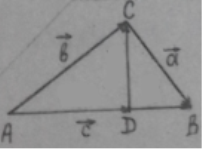Задача 11. Довести, що катет прямокутного трикутника є середнє пропорційне між гіпотенузою та його проекцією на гіпотенузу.

Доведення. Використаємо з рисунка те, що , , але , . Тоді . Звідси , або .

 Задача 12. Обчислити кут між векторами і , де і   одиничні взаємно перпендикулярні вектори.

 Розв’язання. . Обчислимо , і .

;

;

;

Тоді ; отже, кут .

Відповідь. .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

В ході даної роботи було розглянуто поняття, які є складовими тем «Декартові координати на площині» та «Вектори на площині», їх властивості та розкрито суть таких методів: координатного, векторного та векторно-координатного.

 Розроблена методика вивчення векторів на координат на площині, що передбачає володіння учнями різними способами розв’язування геометричних задач та вміння обирати найефективніший з них для конкретного прикладу.

 Опрацювавши певну кількість навчально-методичної літератури, в даній роботі було підібрано систему задач, яка може бути складовою системи задач і вправ курсу геометрії основної школи. Це допоможе, не відступаючи від вимог діючої програми, розширити коло здібностей учнів з даної теми.

 В даній роботі ми ознайомилися з діючою програмою з математики основної школи та зробили аналіз діючих підручників, посібників, методичних статей по темі дослідження; ознайомилися з методикою формування таких понять, як  координати та вектори; розглянули формули, що з цими поняттями пов’язані.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНОЇ І РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

1. Болтянский, В.Г. Векторы в курсе геометрии средней школы: пособие для учителей / В.Г.Болтянский, И.М.Яглом. – М.: Учпедгиз, 1962. – 96 с. – 19 к.
2. Боровик, В.Н. Векторно-координатний метод розв’язування геометричних задач на площині та у просторі: навч. посіб. для слухачів Малих академ. наук/ В.Н.Боровик, М.Я.Ігнатенко. – К., 1995. – 116 с.
3. Буковська, О. Сучасний урок-лекція з геометрії на тему: «Вектори на площині та у просторі» / О.Буковська // Математика в школі. – 2008. - №2. – с.14-25.
4. Галатюк, Ю. Векторно-геометричний метод розв’язування задач у процесі творчої пізнавальної / Ю.Галатюк // Фізика в школах України. – 2007. - №17 (вересень). – с.6-10.
5. Гельфанд, И.М. Метод координат / И.М.Гельфанд, Е.Г.Глаголева, А.А.Кириллов. – М.: Наука, 1973. – 82 с. – 3 грн.
6. Герасимчук, Н. Розвязування геометричних задач методом координат / Н.Герасимчук // Математика. – 2011. - № 43 (листопад). – с.8-13.
7. Дороговцев, А.Я. Метод координат / А.Я.Дороговцев, М.Й.Ядренко. – К.: Вища школа, 1972. – 95 с. : черт. – 16 к.
8. Жученко, І.М. Вектори на площині/ І.М.Жученко// Математика в школах України. – 2012. - №6 (лютий) – с.24-27.
9. Зурнаджи, Н.Ю. Застосування векторно-координатного методу до розвязування задач / Н.Ю.Зурнаджи // Математика в школах України. – 2007. - №8 (березень). – с.15-19.
10.  Єршова А.П. Геометрія. 9 клас: підруч. для загальноосвіт. навч. закл. / А.П.Єршова, В.В.Голобородько, О.Ф.Крижановський, С.В.Єршов. – 5-те вид. – Х. : Вид-во «Ранок», 2014. – 256 с.
11.  Кабачна, С.М. Застосування векторів до розвязуванння геометричних задач / С.Кабачна // Все для вчителя. – 2011. - №1. – с.13-14.
12.  Каленок, Т.П. Вектори на площині: (8-й клас)/ Т.П. Каленок // Математика. – 2003. - №9 (березень). – с.9-12.
13.  Качур, Т. Метод координат: програма курсу за вибором / Т.Качур, Л.Зобенько // Математика. – 2011. - № 39 (жовтень). – с.8-11.
14.  Климець, О.П. Вектори на площині: дидактичний матеріал до теми / О.П. Климець // Математика в школах України. – 2013. - №8. – Вкладка.
15.  Колесников, Ю.А. Координаты неизвестны / Ю.А.Колесников. – М.: Изд. ДОСААФ СССР, 1982. – 238 с. – 90 к.
16.  Крайзман, М.Л. Розв’язування геометричних задач методом координат: посіб. для самоосвіти вчителів / М.Л.Крайзман. – К.: Рад. школа, 1983. – 128 с.: іл.
17.  Мерзляк А.Г., Полонський В.Б., Якір М.С. Геометрія: Підручник для 9 кл. загальноосв. навч. закладів. – Х.: Гімназія, 2009. – 272 с.
18.  Мерзляк А.Г., Полонський В.Б., Якір М.С. Математика: Підручник для 6 класу. – Х.: Гімназія, 2016. – 304 с.
19.  Програма для загальноосвітніх навчальних закладів. Математика 5-12 класи. Затверджено міністерством освіти і науки України. – Київ: Ірпінь, 2005.
20.  Слєпкань З. І. Методика навчання математики: Підруч. для студ. мат. спеціальностей пед. навч. закладів. – К.: Зодіак-ЕКО, 2000. – 512 с.
21.  Смогоржевский, А.С. Метод координат / А.С.Смогоржевский. – М.: Гостехиздат, 1952. – 40 с. – (Попул. лекции по математике; Вып. 10). – 06 коп.
22.  Старова, О.О. Вектори на площині / О.О.Старова // Математика в шк..України. – 2015. - №7-8. – С.67-72.
23.  Супрунок, Л.С. Декартові координати  на площині / Л.С.Супрунок // Все для вчителя. – 2012. - №1-2 (січень). – с.65-67.
24.  Ядренко, М.Й. Метод координат: Метод. розробки / М.Й.Ядренко. – К.: КДУ, 1968. – 24 с.
25. Якименко, О. Вектори: урок-розвязування задач з геометрії, 9-й клас / О.Якименко // Математика. – 2015. - №20 (жовтень). – с.9-16.