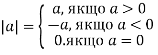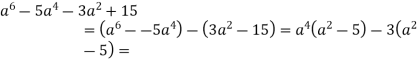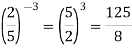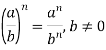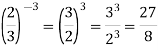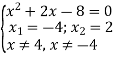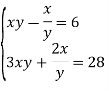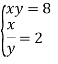Практичний порадник з алгебри "Готуємось до ДПА з математики в 9 класі"
1
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УРАЇНИ
ДАШИНСЬКА ФІЛІЯ ХОРОШІВСЬКОГО ЛІЦЕЮ №1 ЖИТОМИРСЬКОЇ ОБЛАСТІ
Готуємось до ДПА
з математики в 9 класі
Практичний порадник з алгебри

Схвалено на засіданні методичного об’єднання вчителів математики Хорошівського ліцею №1 Житомирської області
Дашинка
2020
Автор:
Андросович Інна Костянтинівна, учитель математики Дашинської філії Хорошівського ліцею №1, учитель вищої категорії.
Укладач:
Андросович Алла Вікторівна
Рецензент:
Мельник Катерина Миколаївна, учитель математики Хорошівського ліцею №2, учитель вищої категорії
Схвалено на засіданні методичного об’єднання вчителів математики, фізики, інформатики (протокол №3 від 19.12.2019)
Андросович І. К. Готуємось до ДПА з математики в 9 класі. Практичний порадник з алгебри. – Дашинка: 2020. – 64 с.
У довіднику узагальнено і систематизовано теоретичний матеріал з курсу математики 5 – 6 класи. та алгебри 7 – 9 кл. До кожного теоретичного розділу подані задачі різного рівня складності з розв’язаннями. Це допоможе учню побачити застосування теоретичного матеріалу. Вдосконалити уміння та навички допоможуть тренувальні вправи, до яких дано відповіді.
Довідник може бути використаний вчителем математики на уроках повторення у 9 кл., також буде корисний учням у підготовці до ДПА.
Зміст
|
|
Вступ………………………………………………... |
5 |
|
1. |
Основи математики………………………………… |
6 |
|
1.1 |
Класифікація чисел………………………………… |
6 |
|
1.2 |
Подільність чисел…………………………………... |
7 |
|
1.3 |
Модуль дійсного числа…………………………...... |
9 |
|
1.4 |
Звичайні дроби……………………………………... |
9 |
|
1.5 |
Пропорція…………………………………………… |
10 |
|
1.6 |
Відсотки…………………………………………….. |
10 |
|
2. |
Многочлен………………………………………….. |
12 |
|
2.1 |
Дії з многочленами………………………………… |
12 |
|
2.2 |
Формули скороченого множення………………..... |
14 |
|
2.3 |
Способи розкладання многочленів на множники |
16 |
|
3 |
Дробово-раціональні вирази………………………. |
18 |
|
3.1 |
Дії з раціональними дробами……………………… |
18 |
|
4 |
Степінь з цілим показником. Властивості степеня……………………………………………… |
25 |
|
5 |
Функції…………………………………………….. |
25 |
|
5.1 |
Поняття функції………………………………….. |
25 |
|
5.2 |
Деякі елементарні функції. Квадратична функція і її властивості…………………………....................... |
27 |
|
6 |
Рівняння…………………………………………….. |
31 |
|
6.1 |
Лінійні рівняння……………………………………. |
31 |
|
6.2 |
Квадратні рівняння………………………………… |
33 |
|
6.3 |
Дробово-раціональні рівняння…………………...... |
37 |
|
7 |
Системи рівнянь і способи їх розв’язання………... |
40 |
|
8 |
Квадратний корінь та його властивості…………... |
47 |
|
9 |
Нерівності і їх системи…………………………….. |
51 |
|
9.1 |
Нерівності. Властивості нерівностей……………... |
51 |
|
9.2 |
Числові проміжки…………………………………... |
52 |
|
9.3 |
Нерівності ІІ степеня………………………………. |
52 |
|
9.4 |
Системи нерівностей із однією змінною…………. |
57 |
|
10 |
Прогресії……………………………………………. |
60 |
|
10.1 |
Арифметична прогресія……………………………. |
60 |
|
10.2 |
Геометрична прогресія…………………………….. |
62 |
|
|
Список використаних джерел……………………... |
64 |
Вступ
Процес підготовки до ДПА сприяє підвищенню якості освіти і запобігає зниженню рівня успішності учня.
Основними складовими готовності учнів до ДПА є знання фактичного матеріалу з основних тем і розділів шкільного курсу з математики, сформованість основних знань, умінь, навичок.
Готувати учнів до ДПА потрібно під час навчального процесу. Бажано вносити зміст уроків у 9 кл. елементи повторення теоретичного і практичного матеріалу.
Пропонований посібник має на меті допомогти вчителеві ефективно організувати повторення навчального матеріалу, а учням удосконалити уміння і навички перед здачею ДПА.
-
Основи математики
- Класифікація чисел
|
|
Означення |
Приклад |
|
Дійсні числа, позначаються R |
Натуральні числа – це числа, які використовуються для лічби предметів. N – позначення множини натуральних чисел |
1; 2; 3; ….. 9; 10; 11; 12;… |
|
Цілі числа – це натуральні числа, їм протилежні і число 0. Z – позначення цілих чисел |
… -3; -2;-1; 0; 1; 2; 3 … |
|
|
Раціональні числа – це числа, які можна подати у вигляді |
|
|
|
Ірраціональні числа – це числа, які не можна подати у вигляді |
|
- Подільність чисел
|
Означення |
Приклади |
|
Дільником числа називається таке число, на яке ділиться дане число.
НСД чисел називається найбільше число, на яке ділиться кожне з даних чисел.
Алгоритм знаходження НСД:
|
8 дільник 16, тому що 16
НСД (44;132)
44=
132=
НСД (44;132)=
|
|
Кратним числа називається таке число, яке ділиться на дане число.
НСК називається найменше число, яке ділиться на кожне з даних чисел.
Алгоритм знаходження НСК:
|
45 кратне 5, тому що 45
НСК(95;114) 95=5∙19 114=2∙3∙19
НСК(95;114)=2∙3∙19∙5==570
|
Ознаки подільності
|
Число ділиться на |
2 |
Якщо закінчується парною цифрою (0;2;4;6;8) |
|
5 |
Якщо закінчується 0 або 5 |
|
|
10 |
Якщо закінчується нулем |
|
|
3 |
Якщо сума цифр, з яких складається число, ділиться на 3 |
|
|
9 |
Якщо сума цифр, з яких складається число, ділиться на 9 |
|
|
4 |
Якщо число, складене з двох останніх цифр, ділиться на 4 |
|
|
8 |
Якщо число, складене з трьох останніх цифр, ділиться на 8 |
|
|
25 |
Якщо число, складене з двох останніх цифр, ділиться на 25 |
- Модуль дійсного числа
|
Означення |
Приклад |
|
|
|3,2|=3,2 |-7|=7 |0|=0 |
Геометрична інтерпретація модуля
│ ← |a| → │
![]()
![]()
![]()
a 0 x
- Звичайні дроби
|
Правила |
Приклади |
|
Основна властивість дробу |
|
|
Значення дробу не зміниться, якщо чисельник і знаменник дробу помножити на одне й те ж саме число (вираз), відмінне від 0 |
|
|
Скоротити дріб – означає поділити чисельник і знаменник дробу на спільний дільник |
|
|
Додавання і віднімання дробів |
|
|
|
|
|
Множення дробів |
|
|
|
|
|
Ділення дробів |
|
|
|
|
- Пропорції
|
Правила |
Приклади |
|
Пропорція – це рівність двох відношень |
15÷3=35÷7 |
|
Основна властивість пропорції: Добуток крайніх членів пропорції дорівнює добутку середніх її членів |
15∙7=3∙35 |
- Відсотки
Відсоток – це одна сота частина. 1%=![]()
Знаходження відсотків від числа: p% від числа a дорівнює ![]() .
.
Приклад. 18% від числа 75 дорівнює ![]()
Знаходження числа за його відсотком: якщо p% числа дорівнює b, то це число дорівнює ![]() .
.
Приклад. Знайти число 20% якого дорівнює 25.
![]()
Знаходження відсоткового відношення: число a становить ![]() від числа b.
від числа b.
Приклад. Скільки відсотків становить 18 від 72? ![]()
Збільшення на p відсотків: якщо число a збільшити на p%, то одержимо число ![]() .
.
Приклад. Якщо число 125 збільшити на 40%, то одержимо 125∙(1+0,4)=125∙1,4=175
- Многочлен
Многочлен – це сума одночленів.
2.1.Дії з многочленами
|
Означення |
Приклади |
|
Додавання і віднімання многочленів |
|
|
При додаванні і відніманні многочленів користуються правилами розкриття дужок. |
(7х2 – 5х + 3) + (3х2 – 5) = 7х2 – 5х + + 3 + 3х2 – 5 = =10х2 – 5х – 2; (7х2 – 5х + 3) - (3х2 – 5) = 7х2 – 5х + + 3 - 3х2 + 5 = =4х2 – 5х + 8 |
|
Множення одночлена на многочлен |
|
|
Щоб помножити одночлен на многочлен, потрібно одночлен помножити на кожний член многочлена й одержані добутки додати. |
3а2(2аb + 4b3) = = 6a3b + 12a2b3 |
|
Множення многочлена на многочлен |
|
|
Щоб помножити многочлен на многочлен, потрібно кожен член одного многочлена помножити на кожний член іншого многочлена й одержані добутки додати. |
(3x2 – 1)(2x + 5) = 6x3 + 15x2 –
|
Розв’язуємо разом
-
Спростити вираз:
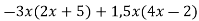
Розв’язання. ![]()
-
Доведіть тотожність:
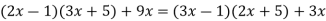
Доведення. Для доведення зручно спростити як ліву, так і праву частини рівності та порівняти результат.
![]()
![]()
![]()
![]()
Тотожними перетвореннями ліву й праву частини рівності звели до одного й того самого вигляду ![]() , тому дана рівність є тотожністю.
, тому дана рівність є тотожністю.
-
Розв’язати рівняння:
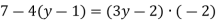
Розв’язання. ![]()
![]()
![]()
![]()
![]()
Тренувальні вправи
-
Спростити вираз.
-
Відповідь. ![]()
Відповідь. ![]()
Відповідь. -15
-
Знайдіть корінь рівняння.
-
Відповідь. -6
Відповідь. 0
- . Формули скороченого множення
|
Формула |
Приклад |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язуємо разом
-
Спростити вираз.
-
Розв’язання. ![]()
![]()
Розв’язання.![]()
- Розв’яжіть рівняння.
![]()
Розв’язання. ![]()
![]()
![]()
![]()
-
Обчисліть зручним способом.
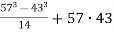
Розв’язання.
![]()
![]()
![]()
Тренувальні вправи
-
Спростити вираз.
-
Відповідь. ![]()
Відповідь. ![]()
Bідповідь. ![]()
-
Розв’яжіть рівняння.
-
Bідповідь. -1,6
Відповідь. 2
- Способи розкладання многочленів
на множники
|
Спосіб |
Приклад |
|
Винесення спільного множника за дужки |
|
|
Спосіб групування |
|
|
Використання формул скороченого множення |
|
|
Застосування кількох способів розкладання на множники |
|
Розв’язуємо разом
-
Розкласти на множники.
-
Розв’язання. ![]()
![]()
Розв’язання. ![]()
![]()
![]()
Розв’язання. ![]()
![]()
![]()
Розв’язання. ![]()
![]()
![]()
![]()
Тренувальні вправи
-
Запишіть вираз у вигляді добутку.
-
Bідповідь. (![]()
Bідповідь. ![]()
Bідповідь. 3(![]()
Bідповідь. ![]()
-
Порівняйте з нулем значення виразу.
-
Bідповідь. ![]()
Bідповідь. ![]()
-
Доведіть, що при будь-якому значенні змінної вираз
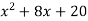 набуває лише додатних значень. Якого найменшого значення набуває цей вирах і при якому значенні
набуває лише додатних значень. Якого найменшого значення набуває цей вирах і при якому значенні 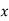 .
.
Відповідь. Найменше значення виразу дорівнює 4 при
![]()
- Дробово-раціональні вирази

- Дії з раціональними дробами
|
Алгоритм |
Приклад |
|
Скорочення дробів |
|
|
Розкласти на множники чисельник і знаменник дробу. |
|
|
Знайти спільний множник чисельника і знаменника. |
|
|
Поділити чисельник і знаменник дробу на спільний множник. |
скоротимо на |
|
Додавання і віднімання дробів |
|
|
При додаванні (відніманні) дробів з різними знаменниками треба:
|
|
|
Множення дробів |
|
|
|
|
|
Ділення дробів |
|
|
|
|
Розв’язуємо разом
-
Скоротити дріб.
-
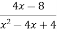
Розв’язання.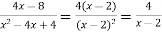
-
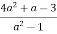
Розв’язання.
-
За формулою ![]() , де
, де ![]() – корені квадратного тричлена розкладемо чисельник на множники
– корені квадратного тричлена розкладемо чисельник на множники
![]()
![]()
![]() ,
, ![]()
![]()
![]()
-
Спростити вираз.
-
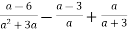
Розв’язання.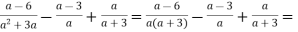
-
=![]()
-
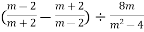
Розв’язання.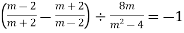
![]() ;
;
![]()
-
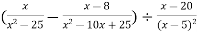
Розв’язання.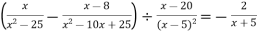
![]()
![]() ;
;
![]()
Тренувальні вправи
-
Довести, що при всіх допустимих значеннях змінної, значення виразу не залежить від значення a.
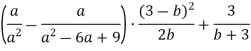
Відповідь. Значення виразу дорівнює 0. Отже, не залежить від значення а.
-
Доведіть тотожність.
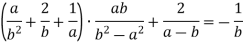
-
Спростити вираз.
-
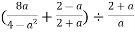
Відповідь.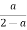 .
.
-
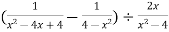
Відповідь.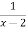 .
.
-
- Степінь з цілим показником. Властивості степеня
|
Означення |
Приклади |
|
Степеня з натуральним показником
|
|
|
Степеня с цілим показником.
Якщо
|
|
|
Властивості |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язуємо разом
-
Відомо, що
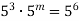 . Знайти
. Знайти 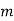 .
.
Розв’язання. Так як при множенні степенів з однаковими основами показники додаються, то
![]() .
.
-
Спростіть вираз.
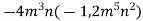
Розв’язання. ![]()
-
Скоротіть дріб.
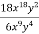
Розв’язання. ![]()
- Виконайте піднесення до степеня.
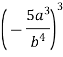
Розв’язання. ![]()
- Подайте у вигляді дробу вираз:
![]()
Розв’язання. ![]()
-
Знайдіть добуток:
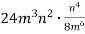
Розв’язання. ![]()
- Виконайте ділення.
![]()
Розв’язання. ![]()
Тренувальні вправи
-
Скоротіть дріб:
-
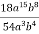 Bідповідь.
Bідповідь. 
-
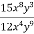 Bідповідь.
Bідповідь. 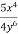
-
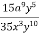 Bідповідь.
Bідповідь. 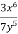
-
-
Виконайте піднесення до степеня.
-
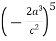 Bідповідь.
Bідповідь. 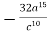
-
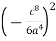 Bідповідь.
Bідповідь. 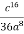
-
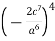 Bідповідь.
Bідповідь. 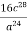
-
-
Виконайте множення.
-
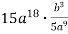 Bідповідь.
Bідповідь. 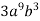
-
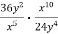 Bідповідь.
Bідповідь. 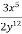
-
-
Подайте у вигляді степеня вираз
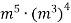
Bідповідь. ![]()
- Функції
5.1 Поняття функції
Функцією називається залежність змінної ![]() від змінної
від змінної ![]() , при якій кожному значенню
, при якій кожному значенню ![]() відповідає єдине значення
відповідає єдине значення ![]() .
.
Область визначення функції ![]() –ті значення, яких може приймати змінна
–ті значення, яких може приймати змінна ![]() (аргумент).
(аргумент).
Множина значень функції ![]() ті значення, яких може приймати змінна
ті значення, яких може приймати змінна ![]() .
.
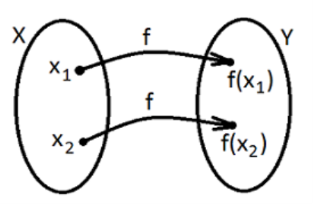
x - аргумент y – значення функції
![]() – область визначення функції
– область визначення функції ![]() – множина значень
– множина значень
Розв’язуємо разом
-
Яка область визначення функції:
-
Розв’язання. Область визначення складається з чисел, при яких ![]() . Знайдемо, при яких
. Знайдемо, при яких ![]() знаменник не перетворить в 0.
знаменник не перетворить в 0.
![]()
![]()
![]()
![]()
![]()
![]() – всі дійсні числа, крім 0 і 3.
– всі дійсні числа, крім 0 і 3.
Розв’язання. Дана функція визначена, якщо підкореневій вираз додатний, тобто ![]()
![]()
![]()
![]()
![]()
-
Знайдіть область значень функції
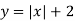 .
.
Розв’язання. Область значень функції – це ті значення, яких може набувати змінна ![]() .
. ![]() . Отже,
. Отже, ![]() .
.
Тренувальні вправи
-
При яких значеннях
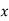 визначена функція.
визначена функція.
-
Bідповідь.![]() всі числа, крім -2 і 2
всі числа, крім -2 і 2
Bідповідь. ![]() всі дійсні числа
всі дійсні числа
Bідповідь. ![]()
Bідповідь. ![]()
Bідповідь. ![]() - всі числа, крім 3
- всі числа, крім 3
-
Знайдіть область значень функції.
-
Bідповідь. ![]()
Bідповідь. ![]()
5.2. Деякі елементарні функції. Властивості квадратичної функції
-
Лінійна:
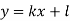
-
Обернено пропорційна
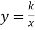
-
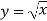 арифметичний квадратний корінь
арифметичний квадратний корінь
-
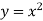
Властивості квадратичної функції:
![]()
- Область визначення – (-∞;+∞)
-
Область значень:
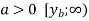 ;
; 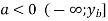
-
Графік – парабола з вершиною у точці
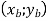 ,
,
де ![]()
![]() – вітки направлені вгору
– вітки направлені вгору
![]() – вітки направлені вниз
– вітки направлені вниз
-
Нулі функції: корені рівняння
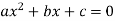
- Зростає на проміжку:
![]()
![]()
- Спадає на проміжку:
![]()
![]()
- Найбільше значення функції:
![]() – не існує
– не існує
![]()
![]()
- Найменше значення функції:
![]() -
- ![]()
![]() – не існує
– не існує
Розв’язуємо разом
-
Пряма
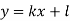 проходить через точки A(4;1) і B(-6;-4). Знайти значення k і l.
проходить через точки A(4;1) і B(-6;-4). Знайти значення k і l.
Розв’язання. Оскільки пряма ![]() проходить через точки A(4;1) і B(-6;-4), то їх координати задовольняють рівняння прямої. Підставимо в рівняння
проходить через точки A(4;1) і B(-6;-4), то їх координати задовольняють рівняння прямої. Підставимо в рівняння ![]() замість
замість ![]() абсцису кожної точки, а замість
абсцису кожної точки, а замість ![]() – ординату кожної точки і складемо систему рівнянь маємо:
– ординату кожної точки і складемо систему рівнянь маємо:
![]()
Розв’яжемо її.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- Яка абсциса точки перетину графіків функцій
![]() і
і ![]() ?
?
Розв’язання. Абсциса точки перетину функцій![]() і
і ![]() є коренем рівняння
є коренем рівняння ![]() .
.
Розв’яжемо одержане рівняння:
![]()
![]()
![]()
![]()
-
Не виконуючи побудови знайти у яких точках перетинає осі координат графік функції
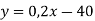 .
.
Розв’язання. Точка перетину графіка функції з віссю абсцис належить цій осі, отже, її ордината дорівнює нулю. Тому для пошуку точки достатньо у формулу, якою задано функцію, підставити значення ![]() і розв’язати одержане рівняння.
і розв’язати одержане рівняння.
![]()
![]()
![]()
![]()
(200;0) – точка перетину з віссю x
Точка перетину графіка з віссю ординат належить цій осі, отже, абсциса такої точки має дорівнювати нулю. Тому для знаходження точки достатньо у формулу, якою задано функцію, підставити значення ![]() , та виконати обчислення.
, та виконати обчислення.
![]()
(0;-40) – точка перетину з віссю у.
-
Знайти нулі функції
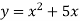 .
.
Розв’язання. Нулі функції – це значення ![]() , при яких
, при яких ![]() . Маємо рівняння
. Маємо рівняння
![]() звідси
звідси ![]()
-
Довести, що функція
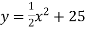 не має нулів.
не має нулів.
Розв’язання. Оскільки ![]() при будь-якому значенні
при будь-якому значенні ![]() , то
, то ![]() , тобто не існує значення
, тобто не існує значення ![]() при яких то
при яких то ![]() . Отже, функція не має нулів.
. Отже, функція не має нулів.
Тренувальні вправи
-
Знайдіть координати точок перетину параболи
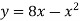 з віссю абсцис.
з віссю абсцис.
Відповідь. (0;0) (8;0)
-
Знайдіть проміжок зростання функції
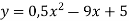
Відповідь. (4,5;0)
-
Знайдіть найбільше значення функції
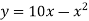 .
.
Відповідь. 25
-
Побудуйте графік функції
 . Користуючись побудованим графіком, знайдіть проміжок, на якому функція зростає, і проміжок, на якому функція спадає.
. Користуючись побудованим графіком, знайдіть проміжок, на якому функція зростає, і проміжок, на якому функція спадає.
Відповідь. Зростає, якщо ![]() . Спадає, якщо
. Спадає, якщо ![]()
-
Побудуйте графік функції
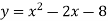 . Користуючись графіком знайдіть:
. Користуючись графіком знайдіть:
- Множину значень функції.
Відповідь. ![]()
-
При яких значеннях
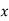 функція набуває від’ємних значень.
функція набуває від’ємних значень.
Bідповідь. ![]()
-
Рівняння
- Лінійне рівняння
Лінійне рівняння – це рівняння, що має вигляд ![]() , де
, де ![]() числа,
числа, ![]() – змінна.
– змінна.
Розв’язання багатьох рівнянь є зведенням цих рівнянь до лінійних шляхом рівносильних перетворень за властивостями рівнянь.
|
Алгоритм |
Приклад |
|
|
|
Розв’язуємо разом
-
Розв’язати рівняння
-
Розв’язання. ![]()
![]()
![]()
Розв’язків немає.
Розв’язання.![]()
![]()
![]()
![]()
![]()
![]() - будь-яке число
- будь-яке число
Розв’язання. ![]() /∙6
/∙6
![]()
![]()
![]()
![]()
![]()
Тренувальні вправи
-
Знайдіть корінь рівняння.
-
Bідповідь.![]()
Відповідь. ![]()
Bідповідь. ![]()
Bідповідь. 3
Bідповідь. 6
Відповідь. -2,5
- Квадратні рівняння
|
Означення |
Приклад |
|
Рівняння виду |
|
|
Неповні квадратні рівняння |
|
|
Якщо в квадратному рівнянні хоч один з коефіцієнтів дорівнює 0, то дане рівняння називається неповним |
|
|
Розв’язання неповних квадратних рівнянь |
|
|
Один розв’язок |
|
|
Спосіб розв’язання: розкласти на множники способом винесення спільного множника за дужки. Два розв’язки. |
|
|
коренів немає, якщо |
коренів немає |
|
Для розв’язання квадратного рівняння знаходимо дискримінант - |
|
|
|
|
|
|
|
|
Дійсних коренів немає
|
|
|
Якщо
|
|
|
Якщо
|
|
Розв’язуємо разом
-
Розкласти квадратний тричлен на множники.
-
Розв’язання. Формула розкладання на множники квадратного тричлена:
де ![]() - корені квадратного тричлена
- корені квадратного тричлена
![]()
![]()
![]()
![]()
![]()
Розв’язання. ![]()
![]()
![]()
![]()
![]()
-
Спростити дріб.
-
Розв’язання. Розкладемо чисельник на множники.
![]()
![]()
![]()
![]()
![]() , тоді
, тоді
![]()
- Розв’язати задачу.
Знайти площу прямокутника, якщо сума його двох непаралельних сторін дорівнює 14см, а діагональ дорівнює 10см.
Розв’язання.
![]() прямокутний, тому складемо рівняння застосувавши теорему Піфагора
прямокутний, тому складемо рівняння застосувавши теорему Піфагора
![]() .
.
 А B
А B
![]()
![]()
![]()
![]()
D C
Розв’яжемо його.
![]()
![]() /÷2
/÷2
![]()
![]()
Отже, ![]() , або
, або ![]()
![]() .
.
![]()
Тренувальні вправи
-
Знайти корінь рівняння.
-
Відповідь. 0,2
Відповідь. 3; ![]()
Відповідь. 7; -4
-
Розкласти квадратний тричлен на множники.
-
Відповідь. ![]()
Відповідь. ![]()
-
Скоротити дріб.
-
Відповідь. ![]()
Відповідь.![]()
Відповідь. ![]()
-
Розкладіть на множники многочлен.
-
Bідповідь. ![]()
Bідповідь.![]()
- Дробово-раціональні рівняння
|
Означення |
Приклад |
|
Раціональне рівняння, що містить дробовий вираз, називають дробово-раціональним рівнянням |
|
|
Алгоритм розв’язання |
|
|
Відповідь: 2 |
Розв’язуємо разом
- Розв’язати задачу. Із села на станцію вийшов пішохід. Через 36 хв після нього з цього села виїхав у тому самому напрямку велосипедист, який наздогнав пішохода на відстані 6 км від села. Знайти швидкість пішохода, якщо вона на 9 км/год менша від швидкості велосипедиста.
Розв’язання. Позначимо ![]() км/год – швидкість пішохода, тоді
км/год – швидкість пішохода, тоді ![]() км/год швидкість велосипедиста.
км/год швидкість велосипедиста. ![]() год – час руху пішохода,
год – час руху пішохода, ![]() год – час руху велосипедиста.
год – час руху велосипедиста. ![]()
Складаємо і розв’язуємо рівняння
![]()
![]()
![]()
![]()
![]() – умову задачі не задовольняє. Отже, швидкість пішохода 6 км/год
– умову задачі не задовольняє. Отже, швидкість пішохода 6 км/год
Відповідь. 6 км/год
Тренувальні вправи
-
Розв’язати рівняння.
-
Bідповідь. -2
Bідповідь. 2,5
Bідповідь. -1
Bідповідь. 1,5
Bідповідь. 9
- Розв’язати задачу. Катер пройшов 10 км за течією річки і 9 км по озеру, витративши на весь шлях одну годину. Знайдіть власну швидкість катера, якщо швидкість течії річки становить 2 км/год.
Відповідь. 18 км/год.
- Системи рівнянь
і способи їх розв’язання
|
Означення |
Приклад |
|
Системою рівнянь називають два або декілька рівнянь, у яких потрібно знайти всі спільні розв’язки. |
|
|
Способи розв’язання систем |
|
|
Спосіб підстановки
|
5x+3+6x=-19 11x=-19-3 11x=-22 x=-2 y=-1-2∙(-2)=3 Відповідь (-2; 3)
|
|
Спосіб додавання Спосіб додавання застосовують якщо коефіцієнти при одній із змінних - протилежні числах.
|
-16y=48 y=-3
5x-3∙3=1 5x=10 x=2
Відповідь: (2;-3)
|
|
Спосіб заміни змінних
|
Відповідь: (4; 2) (-4; -2) |
Розв’язуємо разом
-
Розв’язати систему
-
З рівняння I степеню виражаємо змінну x через y і підставляємо у II рівняння
![]()
![]()
3y2 – 2y2 – y – 2 = 0
y2 – y – 2=0
![]()
x1 = 2 ∙ 2+ 1 = 5
x2 = 2 ∙ (-1)+ 1 = -1
Відповідь. (5; 2) (-1; -1)
Розв’язання. Позначаємо ![]()
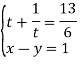
Розв’яжемо одержане рівняння з одним невідомим.
![]()
![]()
![]()
![]()
Тоді повертаємося до введеного позначення.
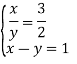
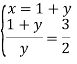
![]()
![]()
![]()
![]()
(3;2)
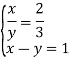
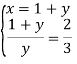
![]()
![]()
![]()
(-1;-3)
Відповідь. (3;2) (-1;-3)
- Розв’язати задачу.
Двоє робітників можуть виконати завдання, працюючи разом, за 2 дні. За скільки днів може виконати це завдання кожний робітник, працюючи самостійно, якщо одному з них для виконання ![]() завдання треба на 3 дні менше, ніж іншому для виконання
завдання треба на 3 дні менше, ніж іншому для виконання ![]() завдання?
завдання?
Розв’язання.
Позначимо, що за ![]() днів може виконати завдання І робітник, працюючи окремо, за
днів може виконати завдання І робітник, працюючи окремо, за ![]() днів – ІІ робітник. Тоді І робітник за один день виконає
днів – ІІ робітник. Тоді І робітник за один день виконає ![]() частину завдання, ІІ -
частину завдання, ІІ - ![]() . Працюючи разом вони за один день виконають
. Працюючи разом вони за один день виконають ![]() завдання.
завдання.
Складемо рівняння ![]() .
.
![]() (днів) – час, необхідний для виконання
(днів) – час, необхідний для виконання
![]() завдання І робітником
завдання І робітником
![]() (днів) - час, необхідний для виконання
(днів) - час, необхідний для виконання
![]() завдання ІІ робітником
завдання ІІ робітником
Складаємо друге рівняння ![]() .
.
Система: 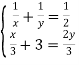
Розв’язуємо її.
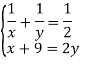
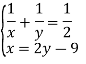
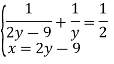
Розв’яжемо рівняння з одним невідомим.
![]()
![]()
![]()
![]()
![]()
Знайдемо відповідні значення ![]() .
.
![]()
![]()
(3;6) (-12;![]() )
)
Розв’язок (-12;![]() ) умову задачі не задовольняє. Тому за 3 дні може виконати завдання І робітник, працюючи окремо, за 6 днів – другий.
) умову задачі не задовольняє. Тому за 3 дні може виконати завдання І робітник, працюючи окремо, за 6 днів – другий.
Відповідь. 3 дні, 6 днів.
Тренувальні вправи
-
Розв’язати систему
-
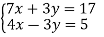 Відповідь. (2;1)
Відповідь. (2;1)
-
1.2 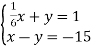 Відповідь. (-12;3)
Відповідь. (-12;3)
1.3 ![]() Відповідь. (-1;-8) (5;4)
Відповідь. (-1;-8) (5;4)
1.4 ![]() Відповідь. (2;4) (-14;20)
Відповідь. (2;4) (-14;20)
1.5 ![]() Відповідь. (3;4) (4;2)
Відповідь. (3;4) (4;2)
1.6 ![]() Відповідь. (1;4) (4;1)
Відповідь. (1;4) (4;1)
1.7 ![]() Відповідь. (-2;-1) (5;
Відповідь. (-2;-1) (5;![]() ) (-5;-
) (-5;-![]() ) (2;1)
) (2;1)
- Розв’язати задачу.
Із села А в село В, відстань між якими дорівнює 24 км, виїхав перший велосипедист. Через 15 хвилин після цього із села В в село А виїхав другий велосипедист. Вони зустрілися через 1 год після виїзду першого велосипедиста. Знайдіть швидкість кожного велосипедиста, якщо перший з них проїжджає за 2 години на 6 км менше, ніж другий за 3 години.
Відповідь. 15 км/год, 12 км/год
- Квадратні корені та їх властивості. Перетворення виразів з коренями
Арифметичним квадратним коренем з числа ![]() називають невід’ємне число, квадрат якого дорівнює
називають невід’ємне число, квадрат якого дорівнює ![]() . Вираз
. Вираз ![]() має зміст якщо
має зміст якщо ![]() .
.
|
Властивості |
Приклади |
|
|
|
|
|
|
|
|
= |
|
|
|
|
Розв’язуємо разом
- Спростити вираз.
1.1 ![]()
Розв’язання. ![]()
![]()
Розв’язання. ![]()
Розв’язання. ![]() , оскільки
, оскільки ![]()
Розв’язання.
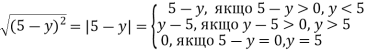
-
Обчисліть:
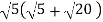
Розв’язання. ![]()
-
Скоротити дріб:
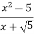
Розв’язання. ![]()
Тренувальні вправи
-
Спростити вираз.
-
Відповідь. (![]() )
)
Відповідь. (![]() )
)
-
Обчислити.
-
Відповідь. 9
Відповідь. -5
Відповідь. ![]()
Відповідь. 2
-
Скоротити дріб.
-
Відповідь. ![]()
Відповідь. ![]()
Відповідь. ![]()
-
Звільнитися від ірраціональності в знаменнику дробу.
-
Відповідь. ![]()
Відповідь. ![]()
-
Нерівності і їх системи
- Нерівності. Властивості нерівностей
|
Означення |
Приклад |
|
|
9 < 12, -3 > -7, 8 ≥ 8 |
|
Властивості |
|
|
Якщо |
5 > 3; 3 > 2, то 5 > 2 |
|
Якщо |
9 > 8, то 8 < 9 |
|
Якщо
|
9 > 11, то 9+2 > 11+2 |
|
Якщо
Якщо |
8 > 5, то 8∙2 > 5∙2 7 > 4, то 7∙(-2) < 4∙(-2) |
|
Якщо
то |
(3 > 2) і (6 > 5), то 9 >7 |
|
Якщо |
8 > 5, то |
|
Якщо |
|
- Числові проміжки
|
Запис за допомогою нерівності |
Геометрична інтерпретація |
Позначення |
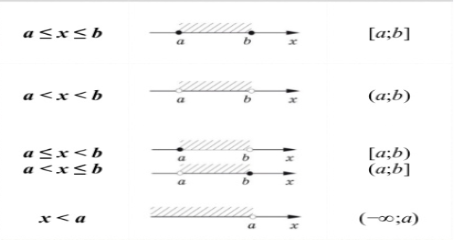
- Нерівності ІІ степеня
Нерівності другого степеня з однією змінною – це нерівності, що мають вигляд ![]() або
або
![]()
Розв’язування нерівностей ІІ степеня з однією змінною можна розглядати як знаходження проміжків, на яких відповідна квадратна функція набуває додатних або від’ємних (недодатних або невід’ємних) значень.
При розв’язанні нерівностей використовують властивості нерівностей.
Розв’язуємо разом
-
Розв’язати нерівність.
-
Розв’язання. ![]()
![]()
![]()
![]()
![]()
![]()
Розв’язання. Помножимо обидві частини нерівності на 36 – найменший спільний знаменник дробів.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Розв’язання. ![]()
![]()
![]()
Оскільки чисельник дробу 5 > 0, то нерівність правильна при ![]() .
.
![]() (2; ∞)
(2; ∞)
Розв’язання. ![]()
![]()
![]()
![]()
![]()
![]() 1;1,5)
1;1,5)
Розв’язання.
![]() або
або ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Розв’язання. Зведемо дану нерівність до виду
![]()
![]()
![]()
![]()
Розглянемо функцію ![]() .
.
Область визначення функції ![]() ,
, ![]() Графіком функції є парабола, вітки якої напрямлені вгору. Знайдемо корені рівняння.
Графіком функції є парабола, вітки якої напрямлені вгору. Знайдемо корені рівняння.
![]()
![]()
![]() абсциси точок перетину параболи з віссю x
абсциси точок перетину параболи з віссю x
![]()
![]()
![]() + - + x
+ - + x
![]()
-4 6
- Знайти область визначення функції:
![]()
Розв’язання. Для знаходження області визначення розв’яжемо нерівність
![]()
![]()
![]() вітки параболи напрямлені вгору
вітки параболи напрямлені вгору
![]()
![]()
![]()
![]()
![]()
![]() + - + x
+ - + x
![]() 3
3 ![]()
Тренувальні вправи
-
Розв’язати нерівність.
-
Bідповідь. ![]()
Bідповідь. (-∞; 3,5)
Bідповідь. [0,5; 2]
Bідповідь. ![]()
Bідповідь. (4; ∞)
- Знайти найбільший цілий розв’язок нерівності:
![]()
Bідповідь. 0
-
При яких значеннях рівняння
 не має коренів?
не має коренів?
Відповідь. (-12;12)
-
Знайти область визначення функції
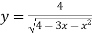 .
.
Bідповідь. ![]()
-
Доведіть, що при всіх дійсних значеннях
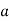 виконується нерівність
виконується нерівність 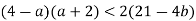 .
.
- Системи нерівностей з однією змінною
|
Означення |
Приклади |
|
Якщо необхідно знайти спільні розв’язки двох чи більше нерівностей з однією змінною, це означає, що треба розв’язати систему двох чи більше нерівностей з однією змінною. |
|
Розв’язуємо разом
- Розв’язати систему нерівностей:
![]()
Розв’язання.
![]()
![]()
![]()
![]()
![]()
- Скільки цілих розв’язків має система нерівностей:
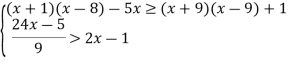
Розв’язання.
![]()
![]()
![]()
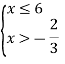
![]()
Цілі числа з проміжку![]() це 0; 1; 2; 3; 4; 5; 6 – сім чисел.
це 0; 1; 2; 3; 4; 5; 6 – сім чисел.
- Розв’язати нерівність.
![]()
Розв’язання цієї системи звести до розв’язання сукупності двох систем.
![]()
![]()
![]()
![]()
![]()
![]()
Розв’язків немає ![]()
- Знайти область визначення функції
![]()
Розв’язання. Область визначення знайдемо, розв’язавши систему:
![]()
![]()
![]()
![]()
![]()
Тренувальні вправи
-
Розв’язати систему нерівностей
-
Bідповідь. ![]()
Bідповідь. (2; 24)
Bідповідь. ![]()
- Знайти область визначення функції
![]()
Bідповідь. ![]()
- Прогресії
10.1. Арифметична прогресія
|
Означення |
Послідовність Наприклад: 3; 5; 7; 9; … d = 2 |
|
Властивість |
|
|
Формула n-го члена |
|
|
Формула суми n перших членів |
|
Розв’язуємо разом
- Знайдіть номер члена арифметичної прогресії 11,8; 12,4; 13; …, який дорівнює 20,8.
Розв’язання. ![]() – дана арифметична прогресія.
– дана арифметична прогресія.
![]() Знайдемо d.
Знайдемо d.
d=12,4-11,8=0,6.
Оскільки ![]() , а за умовою
, а за умовою ![]() , то одержимо рівняння.
, то одержимо рівняння.
20,8=11,8+0,6(n-1), розв’язавши його, знайдемо, що n=16.
- Скільки додатніх членів містить арифметична прогресія 30; 26; 22;…?
Розв’язання. ![]() – арифметична пргресія
– арифметична пргресія
d=26-30=-4. Відомо, що ![]() , то
, то
![]() ,
, ![]() , тобто розв’язати нерівність.
, тобто розв’язати нерівність.
![]()
![]()
![]()
![]()
Отже, останній додатний член має номер n, який менший за 8,5; n – натуральне число, то n=8. Тому всіх додатних членів 8.
- Перший член арифметичної прогресії -4, а різниця 2. Чому дорівнює сума десяти перших членів прогресії?
Розв’язання. ![]()
![]()
Тренувальні вправи
-
Знайти перший член арифметичної прогресії
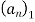 , в якій
, в якій 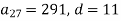 .
.
Bідповідь. 5
-
Знайти різницю арифметичної прогресії
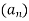 , в якій
, в якій 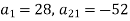
Bідповідь. -4
-
Знайти номер члена арифметичної прогресії
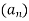 , який дорівнює 46, якщо
, який дорівнює 46, якщо 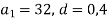 .
.
Bідповідь. 36
-
Знайти суму шістнадцяти перших членів арифметичної прогресії
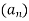 , якщо
, якщо 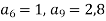 .
.
Відповідь. 40
10.2. Геометрична прогресія
|
Означення |
Послідовність |
|
Властивість |
|
|
Формула n-го члена |
|
|
Формула суми n перших членів |
|
Розв’язуємо разом
-
Знайти перший член геометричної прогресії
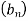 , в якій
, в якій 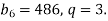
Розв’язання. ![]()
![]()
![]()
-
Чому дорівнює сума перших чотирьох членів геометричної прогресії, перший член якої
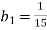 , а знаменник
, а знаменник 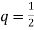 .
.
Розв’язання. ![]()
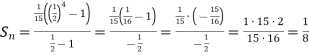
-
Знайти суму шести перших членів геометричної прогресії
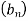 , якщо
, якщо 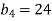 , а знаменник
, а знаменник 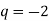 .
.
Розв’язання. ![]() ,
, ![]() .
.
![]()
![]()
![]()
![]()
Тренувальні вправи
-
Знайдіть перший член геометричної прогресії
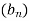 , якщо
, якщо 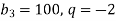 .
.
Відповідь. 25.
-
Знайдіть знаменник геометричної прогресії
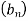 , у якої
, у якої 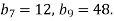
Bідповідь. ![]()
- Між числами 1 і 64 вставте два числа таким чином, щоб вони разом з даними утворили геометричну прогресію.
Відповідь. 4, 16
-
Знайдіть суму чотирьох перших членів геометричної прогресії, перший член якої
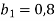 , знаменник q=3.
, знаменник q=3.
Відповідь. 32.
Список використаних джерел
- Андруг Л.М. Алгебра. 19 тижнів до державної підсумкової атестації. 9 клас.- Х.: Країна мрій, 2007. – 208 с.
- Генденштейн Л. Е., Єрошова А. П., Ершова Г.С. Наочний довідник з алгебри та початків аналізу з прикладами для 7-11 класів. –Х.: Гімназія, 1997. – 96 с.
- Титаренко О. М., Роганін О. М., Максименко О. Ю. Математика. Комплексний довідник – Х.: Торсінг плюс, 2009. – 320 с.
- Мерзляк А.Г. [та ін.] Збірник завдань для державної підсумкової атестації з математики 9 клас за ред. Бурди М. І. – К.: Центр навчально-методичної літератури, 2014. – 256 с.
- Чекова А. М. Алгебра і початки аналізу в таблицях. 7 – 11 класи. Навчальний посібник. – Х.: Науково-методичний центр, 2003. – 248 с.
- Кравчук В., Підручна М., Янченко Г. Алгебра, 8 клас за редакцією Слєпкань З. – Т.: Підручники й посібники, 2005. – 232 с.
- Захарійченко Ю.О., Школьний О.В. Збірник завдань для підготовки до ЗНО. – К.: Генеза, 2015. – 168 с.
- Істер О. С. Алгебра 7 клас. – К.: Генеза, 2015. – 256 с.
- Роєва Т.Г. Алгебра. Практикум. 9 клас. – Х.: Країна мрій, 2003. – 48 с.
- Роєва Т.Г., Синельник Л. Я., Кононенко С. А. Алгебра у таблицях, 8 клас. Навчальний посібник. – Х.: Країна мрій, 2004. – 44 с.
- Газета Математика в школах України №8, 2013, №10-12, 2015, №13-15, 2015


про публікацію авторської розробки
Додати розробку