Правила знаходження первісних. 11 клас
Тема. Правила знаходження первісних.
Мета: сформувати вміння та навички знаходження первісних, користуючись таблицею первісних і правилами їх знаходження; розвивати логічне та аналітичне мислення, прагнення до пошуку, уміння користуватись додатковими джерелами інформації; виховувати культуру математичних записів.
І. Перевірка домашнього завдання.
- Наявність письмового завдання перевіряють чергові або консультанти.
- Відповіді на запитання, що виникли в учнів при виконанні домашніх вправ.
Запишіть первісні для функцій:
1)х4; 2) 6х-5; 3)1/х; 4)![]() ; 5)ех; 6)
; 5)ех; 6)![]() х; 7) cosx; 8) sinx; 9) 1/сos2x; 10) 1/sin2x ; 11) x
х; 7) cosx; 8) sinx; 9) 1/сos2x; 10) 1/sin2x ; 11) x![]() 12)sin2x
12)sin2x
Два учні працюють на закритих дошках. Їх роботу перевіряє вчитель. Учні класу здійснюють взаємоперевірку.
Учням пропонується знайти первісні функцій («мозкова атака»):
f(х)=6 sin 4х; f(х)=(1/2![]() ) + (4х)2
) + (4х)2
Учні пропонують різні способи знаходження первісних, а потім відбувається перевірка їх правильності. Переконуємось, що при знаходженні первісних підбиранням функцій, похідна яких дорівнює f(х) виникають труднощі. Виникає запитання: «Чи існують певні правила, за якими первісні легко шукати?»
Учитель повідомляє, що такі правила справді існують і доведено їх істинність. Він пропонує знайти у підручнику ці правила і записати їх у зошити. Учнів по черзі викликають до дошки пояснювати, як вони зрозуміли правила, і розв'язати деякі вправи. Якщо є потреба, то вчитель пояснює сам.
Учні об'єднуються у три різнорівневі групи. Кожна група отримує завдання відповідного рівня складності.
Для даної функції / знайти загальний вигляд первісної:
2) f(x)=10x4+14x6;
3) f(x) = 3cos x – 4/sin2x.
Завдання достатнього рівня
Для даної функції / знайти первісну Р, що задовольняє даній умові:
1 ) f(x) = 6x2+4x-3, F(-2)=-3;
2) f(x) =15x14- 5/4![]() , F(1) = 0;
, F(1) = 0;
3) f(x) = 3 – 1/x2, F(0,5) = 7
Завдання високого рівня
Для даної функції / знайти первісну, графік якої проходить через дану точку А:
-
f(x) = 1/3 sin x/3+4cos4x,A(
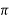 ;3);
;3);
-
f(x) = 2/sin2(4x –
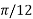 ), A(
), A(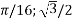 );
);
-
f(x) = 1/
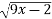 , A(3;1)
, A(3;1)
- Підведення підсумків уроку.
Учитель пропонує ще раз пригадати таблицю та правила знаходження первісних. Відповідає на запитання учнів.
- Домашнє завдання.


про публікацію авторської розробки
Додати розробку
