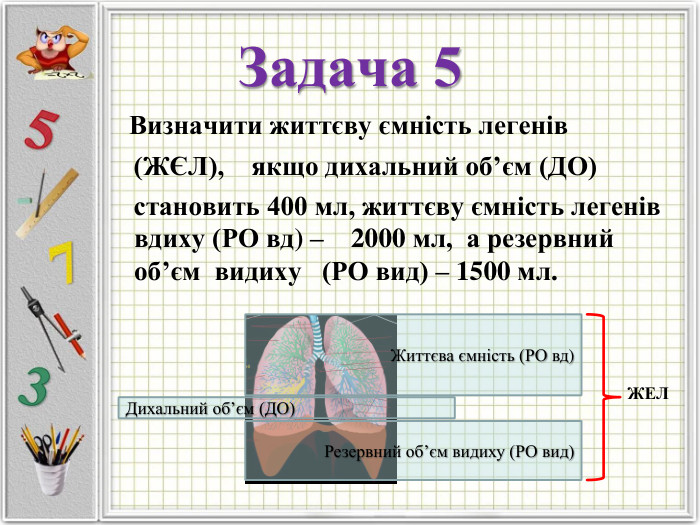
Презентаці "Математичне моделювання"
Про матеріал
Матеріал презентації допоможе провести урок з розв'язання різноманітних прикладних задач Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра 9 клас (Прокопенко Н.С., Захарійченко Ю.О., Кінащук Н.Л.)
До уроку
ПОВТОРЕННЯ НАВЧАЛЬНОГО МАТЕРІАЛУ Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку