Презентації "Перетворення в прострі"

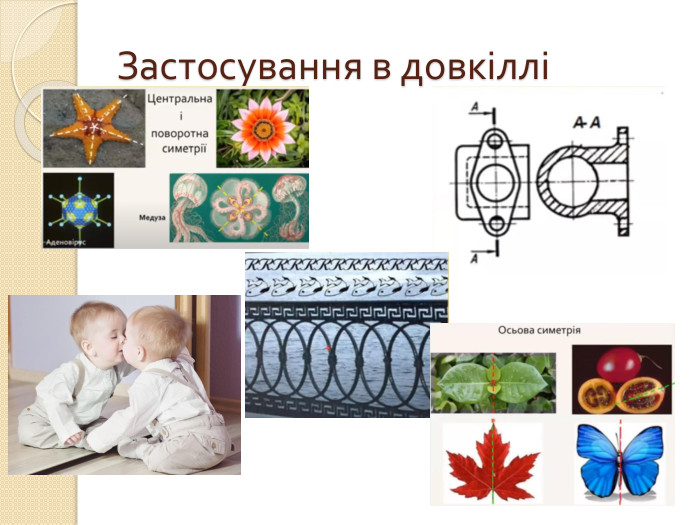
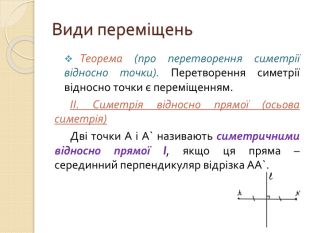
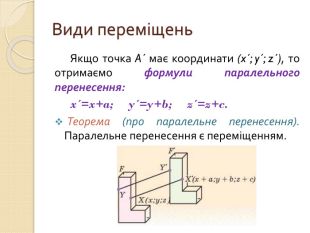
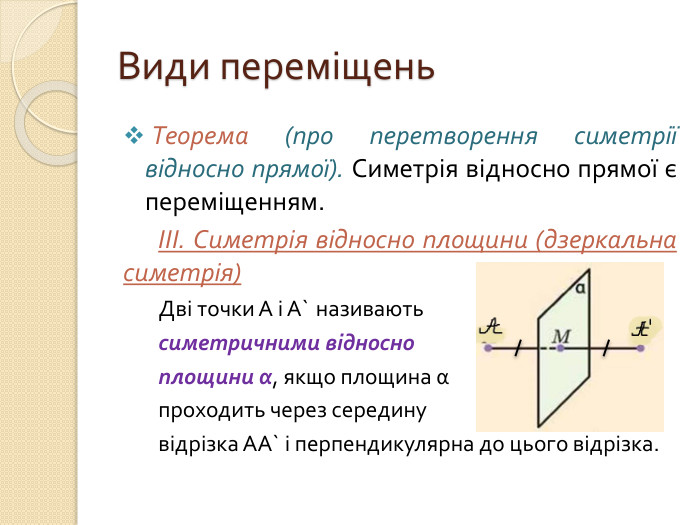
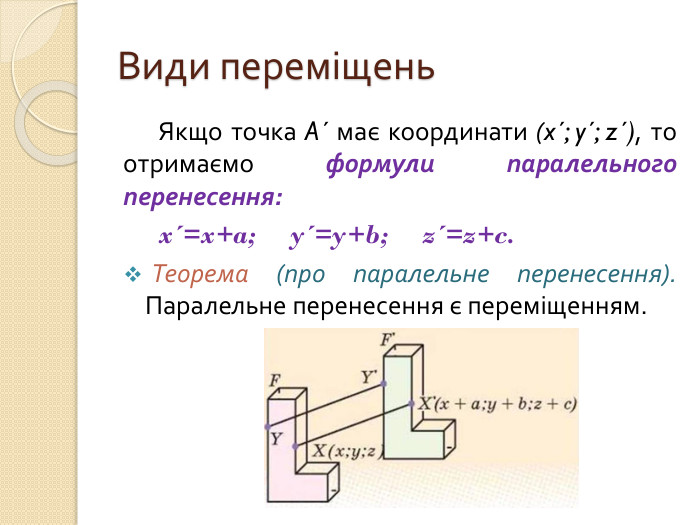
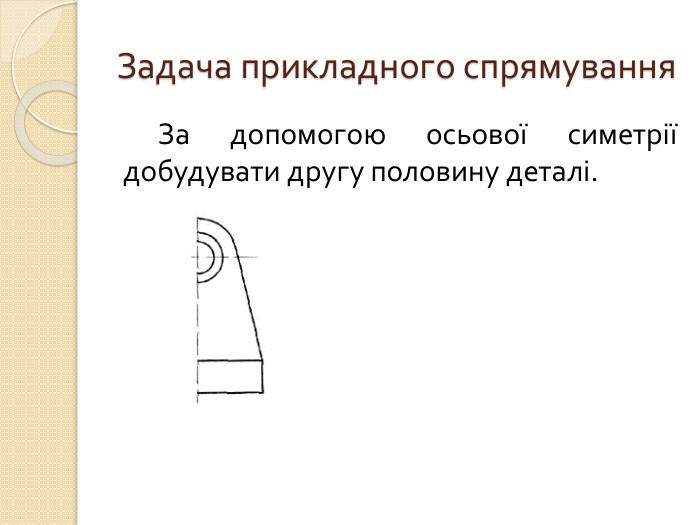
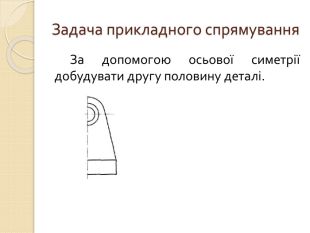
Перетворення в просторі. Рух у просторі, його властивості. Основні види переміщень у просторі Застосування у довкілліРух у просторі, його властивостіВластивості руху. Види переміщень. Розв’язування вправ. Задача прикладного характеру. Підготувала вчителька математики. Анна Литвиненко

Застосування в довкіллі

Рух у просторі, його властивостіПеретворенням однієї фігури і іншу називають переміщенням (рухом), якщо воно зберігає відстань між точками. Властивості переміщення у просторі:під час переміщення точки, що лежать на прямій, переходять у точки, що лежать на прямій, і зберігається порядок їх взаємного розміщення;під час переміщення прямі переходять у прямі, промені – у промені, відрізки – у відрізки;

Властивості руху. Види переміщеньпід час переміщення кут переходить у рівний йому кут;під час переміщення площина переходить у площину.І. Симетрія відносно точки центральна симетрія) Дві точки А і А` називають симетричними відносно точки О, якщо О – середина відрізка АА`.

Види переміщень. Теорема (про перетворення симетрії відносно точки). Перетворення симетрії відносно точки є переміщенням.ІІ. Симетрія відносно прямої (осьова симетрія) Дві точки А і А` називають симетричними відносно прямої l, якщо ця пряма – серединний перпендикуляр відрізка АА`.

Види переміщень Теорема (про перетворення симетрії відносно прямої). Симетрія відносно прямої є переміщенням.ІІІ. Симетрія відносно площини (дзеркальна симетрія)Дві точки А і А` називають симетричними відносно площини α, якщо площина αпроходить через серединувідрізка АА` і перпендикулярна до цього відрізка.

Види переміщень Теорема (про перетворення симетрії відносно площини). Перетворення симетрії відносно площини є переміщенням. IV. Паралельне перенесення. Паралельне перенесення у просторі називають таке перетворення фігури, при якому її довільна точка А(x; y; z) переходить у точку A´(x+a; y+b; z+c), де a, b, c – одні й ті самі числа для всіх точок фігури.

Види переміщень. Якщо точка A´ має координати (x´; y´; z´), то отримаємо формули паралельного перенесення:x´=x+a; y´=y+b; z´=z+c. Теорема (про паралельне перенесення). Паралельне перенесення є переміщенням.

Види переміщень. Перетворення простору, при якому точи прямої а залишаються на місці, а всі інші точки повертаються навколо цієї прямої (в одному і тому ж напрямі) на кут α, називається поворотом, або обертанням.

Розв’язування вправ. Задача 1 Запишіть координати точок, симетричних точці Р(-1; 2; 7) відносно осі: 1) абсцис; 2) аплікат. [1]Розв’язання: Р´(-1; -2; -7) – точка, симетрична точці Р відносно осі абсцис;Р´(1; -2; 7) – точка, симетрична точці Р відносно осі аплікат. Відповідь: 1) Р´(-1; -2; -7); 2) Р´(1; -2; 7) .

Розв’язування вправ. Задача 2 Точки В(2;у;z) і В´(х;-3;8) симетричні відносно площини xz. Знайдіть x; y; z. [1]Розв’язання: Так як точки симетричні відносно площини xz, тоді точка В´ матиме такі координати (x;-y; z). хв= хв´ ; ув= - ув´ ; zв= zв´ Отже, В(2;3;8) і В´(2;-3;8). Відповідь: х=2; у=3; z=8.

Розв’язування вправ. Задача 3 При паралельному перенесенні точка А(1;-1;3) переходить у точку А´(3;-5;2). У яку точку переходить при цьому початок координат? [2]Розв’язання: Підставляючи у формули паралельного перенесення координати точок А і А´, одержуємо рівнянняx´=x+a; 3=1+a; a=2y´=y+b; -5=-1+b; b=-4z´=z+c; 2=3+c; c=-1 Початок координат (0;0;0)Тоді, x´=0+2=2; y´=0-4=-4; с´=0-1=-1. Відповідь: О´(2;-4;-1)

Розв’язування вправ. Задача 4 Точки А і В не належать площині α, а точки А1 і В1 симетричні відповідно точкам А і В відносно площини α. Як розташований відносно площини α вектор:1) АВ+А1 В1;      2) АВ−А1 В1. [1]Розв’язання: 

Розв’язування вправ. Задача 5 Точки А(2;-1;7) і А´(2;3;7) симетричні відносно площини α. Яким є взаємне розташування площини α і осі: 1) абсцис; 2) ординат; 3) аплікат? [1]Розв’язання: Так як, точки А і А´ мають однакові абсциси і аплікати, але різні ординати, то площиною α симетрії цих точок є площина у=1. Отже, площина α паралельна площині xz, а тому вона паралельна і осям абсцис і аплікат, звідси слідує, площина α перпендикулярна осі ординат.

Задача прикладного спрямування. За допомогою осьової симетрії добудувати другу половину деталі.