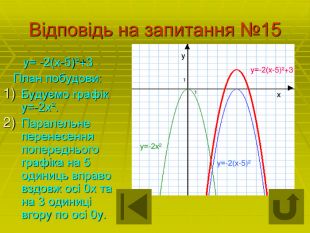
Презентація- вікторина " Перетворення графіків функцій".

Вікторина. Найпростіші перетворення графіків функцій 1 2 3 4 5 6 7 8 9 10 12 13 14 15 11

Запитання №1 Як можна отримати графік функції у=f(х)+в, використовуючи графік функції у=f(х)?

Запитання №2 Які перетворення треба здійснити для графіка функції 5 у=------, щоб отримати графік х 5 у=--------- +7. х-3

Запитання №3 Як можна отримати графік функції у=f(х+а), використовуючи графік функції у=f(х)?

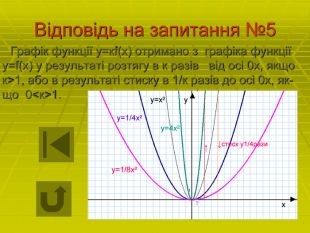
Запитання №4 Дано функції: 1) у=g(х)+3 2) у=|g(х)| 3) у=g(-х) 4) у=3g(х) 5) у=1/3g(х) 6) у=-g(х) 7) у=g(3х) 8) у=g(1/3х) 9) у=g(х) -3 10) у=g(х-3) 11) у=g(х+3) 12) у=g(|х|) Серед даних функцій виберіть такі, графіки яких утворюються з графіка функції у=g(х) паралельним перенесенням на 3 одиниці вниз вздовж осі 0у та стисненням у 3 рази до осі 0х.

Запитання №5 Як можна отримати графік функції у=кf(х), використовуючи графік у=f(х)?

Запитання №6 Як можна отримати графік функції у=f(кх), використовуючи графік у=f(х)?

Запитання №7 Як можна отримати графік функції у=-f(х), використовуючи графік у=f(х)?

Запитання №8 Як можна отримати графік функції у=f(-х), використовуючи графік у=f(х)?

Запитання №9 Як можна отримати графік функції у=|f(х)|, використовуючи графік у=f(х)?

Запитання №10 Як можна отримати графік функції у=f(|х|), використовуючи графік у=f(х)?

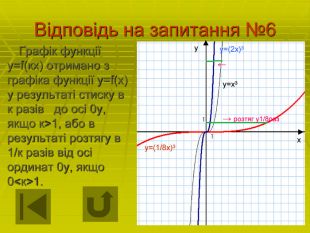
Запитання №11 Дано функції: 1) у=g(х)+3 2) у=|g(х)| 3) у=g(-х) 4) у=3g(х) 5) у=1/3g(х) 6) у=-g(х) 7) у=g(3х) 8) у=g(1/3х) 9) у=g(х) -3 10) у=g(х-3) 11) у=g(х+3) 12) у=g(|х|) Серед даних функцій виберіть такі, графіки яких утворюються з графіка функції у=g(х) розтягненням від осі 0у в 1/3 рази та графік симетричний відносно осі 0х.

Запитання №12 Дано функції: 1) у=g(х)+3 2) у=|g(х)| 3) у=g(-х) 4) у=3g(х) 5) у=1/3g(х) 6) у=-g(х) 7) у=g(3х) 8) у=g(1/3х) 9) у=g(х) -3 10) у=g(х-3) 11) у=g(х+3) 12) у=g(|х|) Серед даних функцій виберіть такі, графіки яких утворюються з графіка функції у=g(х) паралельним перенесенням на 3 одиниці вліво вздовж осі 0х та розтягу від осі 0х в 3 рази.

Запитання №13 Дано функції: 1) у=g(х)+3 2) у=|g(х)| 3) у=g(-х) 4) у=3g(х) 5) у=1/3g(х) 6) у=-g(х) 7) у=g(3х) 8) у=g(1/3х) 9) у=g(х) -3 10) у=g(х-3) 11) у=g(х+3) 12) у=g(|х|) Серед даних функцій виберіть такі, графіки яких утворюються з графіка функції у=g(х) стисканням в 3 рази до осі 0у та графік симетричний графіку у=g(х) відносно осі ординат 0у.

Запитання №14 Задайте формулою функцію, графік якої зображено на рисунку. Вкажіть алгоритм побудови. у ▲ х ► ►

Запитання №15 Для червоного графіка функції вкажіть форму-лу та алгоритм побудови. у ▲ ► х -2 -1

Відповідь на запитання №1 Графік функції у=f(х)+в можна отри-мати в результаті паралельного пере-несення графіка функції у=f(х) на в одиниць угору, якщо в>0, і на –в одиниць униз, якщо в<0. у=√х у=√х+4 у=√х-5 у х ▲ ►

Відповідь на запитання №2 Графік функції у=5/х необхідно перенести вздовж осі 0х на 3 одиниці праворуч, а потім вздовж осі 0у на 7 одиниць вгору. у=5/(х-3)+7 у=5/х у х ▲ ► у' х'

Відповідь на запитання №3 Графік функції у=f(х+а) можна отримати в ре-зультаті паралель-ного перенесення графіка функції у=f(х) на а одиниць уліво, якщо а>0, і на –а одиниць управо, якщо а<0. у ▲ ► х у=(х+3)І у=(х-5)І

Відповідь на запитання №4 9) у=g(х) -3 будуємо паралельним перенесенням на 3 одиниці вниз вздовж осі 0у, 5) у=1/3g(х) будуємо стисненням у 3 рази до осі 0х.

Відповідь на запитання №5 Графік функції у=кf(х) отримано з графіка функції у=f(х) у результаті розтягу в к разів від осі 0х, якщо к>1, або в результаті стиску в 1/к разів до осі 0х, як- що 0<к>1. ► х у ▲ у=хІ у=1/4хІ у=1/8хІ у=4хІ ↑ ↓стиск у1/4рази

Відповідь на запитання №6 Графік функції у=f(кх) отримано з графіка функції у=f(х) у результаті стиску в к разів до осі 0у, якщо к>1, або в результаті розтягу в 1/к разів від осі ординат 0у, якщо 0<к>1. у х ▲ ► ← → розтяг у1/8раз у=хі у=(1/8х)і у=(2х)і

Відповідь на запитання №7 у ▲ х ► у=√х у=-√х ↑ ↓ Усі точки графіка у=-f(х) можна отримати, замінивши точки графіка у=f(х) на точки з тією самою абсцисою і протилежною ординатою. у=f(х) відобразити симетрично відносно осі абсцис 0х.

Відповідь на запитання №8 Усі точки графіка у=f(-х) можна отримати, замінивши точки графіка у=f(х) на точки з такою самою ординатою і протилежною абсцисою. у=f(х) відобразити симетрично відносно осі ординат 0у. у ▲ х ► у=хі у=(-х)і → ←

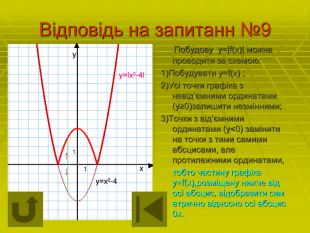
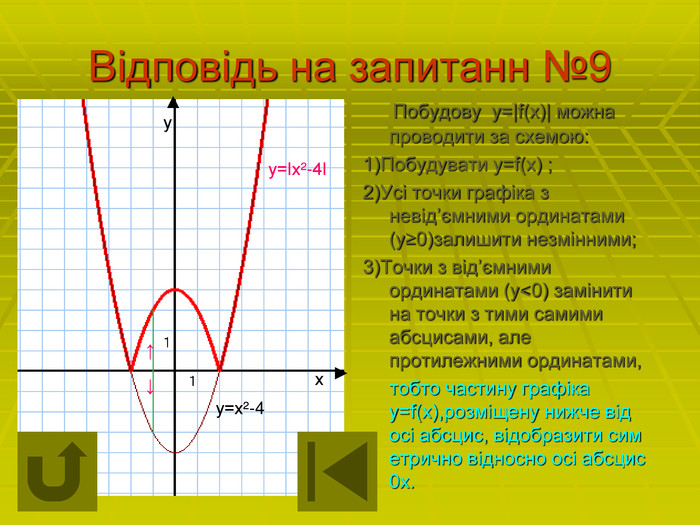
Відповідь на запитанн №9 Побудову у=|f(х)| можна проводити за схемою: 1)Побудувати у=f(х) ; 2)Усі точки графіка з невід’ємними ординатами (у≥0)залишити незмінними; 3)Точки з від’ємними ординатами (у<0) замінити на точки з тими самими абсцисами, але протилежними ординатами, тобто частину графіка у=f(х),розміщену нижче від осі абсцис, відобразити сим етрично відносно осі абсцис 0х. у ▲ х ► у=хІ-4 у=ІхІ-4І ↑ ↓

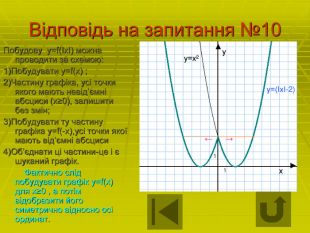
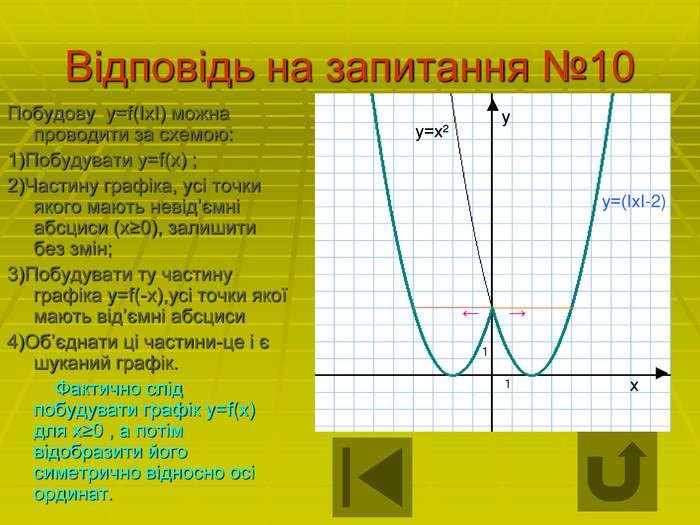
Відповідь на запитання №10 Побудову у=f(ІхІ) можна проводити за схемою: 1)Побудувати у=f(х) ; 2)Частину графіка, усі точки якого мають невід’ємні абсциси (х≥0), залишити без змін; 3)Побудувати ту частину графіка у=f(-х),усі точки якої мають від’ємні абсциси 4)Об’єднати ці частини-це і є шуканий графік. Фактично слід побудувати графік у=f(х) для х≥0 , а потім відобразити його симетрично відносно осі ординат. у ▲ х ► у=хІ у=(ІхІ-2) ← →

Відповідь на запитання №11 Графік 8) у=g(1/3х) будуємо в результаті розтягнення графіка у=g(х) в 1/3 разів від осі ординат 0у. Графік 6) у=-g(х) будуємо симетрично графіку у=g(х) відносно осі абсцис 0х.

Відповідь на запитаня №12 Графік 11) у=g(х+3) будуємо паралельним перенесенням графіка у=g(х) на 3 одиниці вліво вздовж осі 0х. Графік 4) у=3g(х) будуємо в результаті розтягу в 3 рази від осі абсцис 0х.

Відповідь на запитання №13 Графік 7) у=g(3х) будуємо в результаті стиску в 3 рази графіка у=g(х) до осі ординат 0у. Графік 3) у=g(-х) будуємо в результаті симетрії графіка у=g(х) відносно осі ординат 0у.

Відповідь на запитання №14 Побудовано графік у=(х+2)і-4, який отримався в результаті паралельного перенесення графіка у=хі на 2 одиниці вліво по осі 0х та на 4 одиниці вниз по осі 0у.

Відповідь на запитання №15 у= -2(х-5)І+3 План побудови: Будуємо графік у=-2хІ. Паралельне перенесення попереднього графіка на 5 одиниць вправо вздовж осі 0х та на 3 одиниці вгору по осі 0у. у ▲ х ► у=-2хІ у=-2(х-5)І+3 у=-2(х-5)І