Графічний метод розв’язування рівнянь, систем рівнянь, які містять параметри.

 

 

Учитель

Херсонської НВК №33 Херсонської міської ради

Вигоднер Д.І.

 

 

Однією з найважливіших задач, які стоять перед вчителями математики в сучасній диференційованій школі, є розвиток в учнів креативних здібностей, їх творчого мислення.

Творчість це здатність дивуватися й пізнавати, уміння знаходити рішення в нестандартних ситуаціях. Це націленість на відкриття нового і здатність до глибокого усвідомлення свого досвіду.

Кожний учитель має своє уявлення про те, що таке обдарованість дітей. Це уявлення у кожного з нас складається на основі розуміння творчої обдарованості, з досвіду спілкування з дітьми, спостереження за особливостями їхнього розвитку.

Уявлення про обдарованість змінюються залежно від потреб суспільства. Для різних періодів історії були потрібні різні види обдарованості: у прадавні часи особливо високо цінувалися здібності воїнів і підкорювачів інших країн; у середні віки в західній філософії панував ідеал мислителя; у сучасну епоху під обдарованістю найчастіше розуміють здатність долати заплутані життєві колізії, уміння знаходити інноваційні способи вирішення проблем. Це дуже важлива якість в умовах нестабільного світу, що динамічна розвивається. Наш час - це час змін і глобалізації. Тому стає досить важливим, що вийшовши зі стін шкіл у велике життя, молоді люди повинні бути адаптовані до нього.

На жаль, у сучасній системі освіти в Україні пануючим залишається підхід до навчання, як до засвоєння певної суми знань. Дуже часто навчання зводиться до запам’ятовуванняі повторення дій, типових способів розв’язання завдань, до засвоєння знань, умінь, навичок. Але ж вимоги сучасного життя такі, що простого володіння сумою знань недостатньо, необхідна постійна готовність до зміни умов проблемної ситуації й уміння розглянути її з різних точок зору, знайти найбільш раціональний спосіб рішення. От чому розвиток творчих здібностей повинен стати визначальним у системі освіти, метою реалізації різних освітніх програм. Такі програми повинні містити спеціальні завдання, які сприяли б активізації творчих здібностей. Крім того, чим більше ми надаємо дітям можливостей для конструктивної творчості, тим більше ймовірним стає їхнє позитивне самовизначення в процесі формування їх особистісних якостей.

У цій роботі ми показали нестандартний підхід до розв’язування деяких типів задач.

 

І розділ:

Побудова графіків функцій і рівнянь, систем рівнянь, що містять модуль.

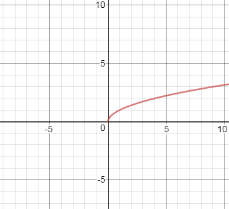
1. Побудова графіка функцій y=f(|x|)

Згідно з означенням модуля маємо:

f(|X|)=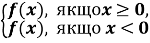

Функція - парна. Для того, щоб дістати графік функції,  необхідно:

побудувати графік функції:;

а) частину його, яка знаходиться ліворуч від осі ординат відкинути, а до тієї частини, що залишилась, добудувати симетричну відносно осі ординат.

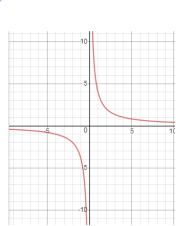
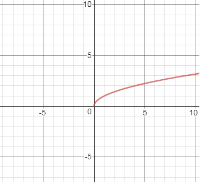
Приклад 1.

Побудувати графік функції:

Розв’язання

а) побудуємо графік функції

б):  виконаємо паралельний перенос осі ординат на одну одиницю вліво;

б) :  частину графіка, яка знаходиться ліворуч осі ординат, відкинемо. А до частини, що залишилась, добудуємо симетричну відносно осі ординат.

Мал.1

 

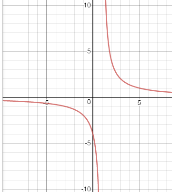
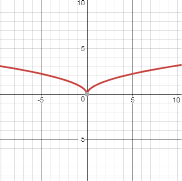
Приклад 2.

Побудувати графік функції

Розв’язання

а) побудуємо графік функції

б) до отриманої кривої добудуємо симетричну відносно осі ординат.

Мал. 2

2. Побудова графіка функції:y=|f(x)|

Функціянабуває тільки невід’ємних значень,тому, щоб дістати графік цієї функції будуємо графік функції і частину його, яка розташована нижче осі абсцис, симетричноввідобразимо відносно осі абсцис.

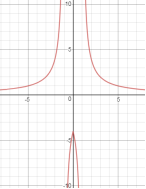
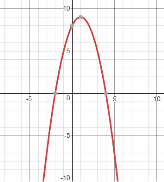
Приклад 1

Побудувати графік функції:

Розв’язання

а). Побудуємо графік функції:,                 (або);

б). Будуємо графік функції:  .

Частину графіка, яка знаходиться нижче осі абсцис симетрично відобразимо відносно осі абсцис.

Мал.3

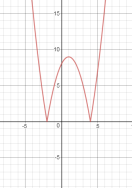
Приклад 2

Побудуйте графік функції:|

Розв’язання

а)  побудуємо графік функції: ;

б) частину графіка, яка розташована нижче осі абсцис, симетрично відобразити відносно осі абсцис;

в)виконаємо паралельний перенос осі ординат на одиниці вправо.

Мал.4

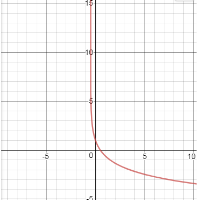
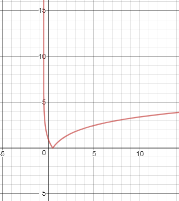
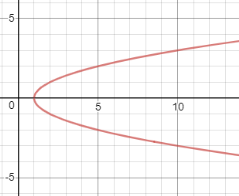
3. Побудова графіка рівняння:;

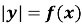На проміжках, дерівняння немає змісту, якщо , то для кожного х і . Щоб побудувати графік рівняння, треба побудувати графік функції ,  частину його, яка розташована нижче осі абсцис відкинути, а до тієї частини, що залишилась добудувати симетричну відносно осі абсцис.

Приклад

Побудувати графік рівняння:

Розв’язання

1. Побудуємо графік функції :

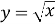
б) Виконаємо паралельний перенос осі ординат на одну одиницю вліво;

в) До отриманої кривої добудуємо криву, симетричну даній, відносно осі абсцис.

Мал.5

 

 

4. Побудова графіка функції:

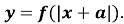
Графік функції  можна дістати , якщо побудувати графік функції ,  частину його, яка знаходиться з лівого боку осі ординат відкинути , а до тої , що залишилась , добудувати симетричну відносно осі ординат на а одиниць вправо, якщо , або на одиниць вліво, якщо  .

 

Приклад

Побудувати графік функції:

Розв’язання

а) побудуємо графік функції

б) до отриманої кривої добудуємо симетричну відносно осі ординат;

в) виконаємо паралельний перенос осі ординат на 2 одиниці вправо.

 

Мал. 6

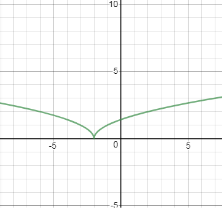
5. Побудова графіка рівняння:

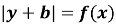
 Графік рівняння можно дістати з графіка функції , якщо частину, яка розташована нижче осі абсцис відкинути, а до тої, що залишилася, добудувати симетричну відносно осі абсцис, після чого виконати паралельнй перенос осі абсцис на в одиниць вгору, якщо, або на |b| одиниць вниз, якщо .

Приклад

Побудувати графік рівняння |у+3|=.

Розв’язання

а) побудуємо графік функції у=;

б) частину його, яка розташована нижче осі абсцис, відкинути, а до тієї, що залишилась, добудувати симетричну відносно осі абсцис;

в) виконаємо паралельний перенос осі абсцис на 3 одиниці вгору.

                                                                                     Мал.7

6. Побудова графіка рівняння:

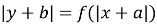
Графік рівняння можна дістати з графіка функції, якщо виконати послідовно перетворення, вказані в пунктах 4 і 5.

Приклад

Побудувати графік функції 

Розв’язання

а) побудуємо графік функції;

б) частоту його, яка знаходиться ліворуч осі ординат, відкинемо, а до тої, що залишилась, добудуємо симетричну відносно осі ординат;

в) до отриманого графіку добудуємо симетричну частину відносно осі абсцис;

г) виконаємо паралельний перенос осі абсцис на 4 одиниці вниз, а вісь ординат переносимо паралельно на 1 одиницю вправо

 Мал. 8

 

 

 

 

 

 

 

 

 

 

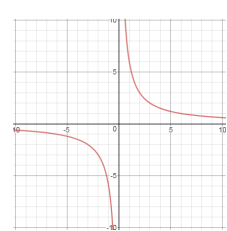
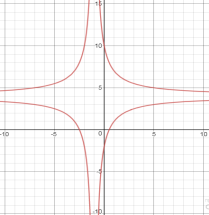
2 розділ                                                                        Приклади розв’язування рівнянь, систем рівнянь, нерівностей, які містять параметри.

Приклад 1.

Скільки розв’язків має рівняння, в залежності від параметра ?

Розв’язання

Розв’яжемо рівняння графічним методом. Для цього будуємо графіки функцій:i.    

План побудови першої функції:

1);2);;3).

Мал. 9

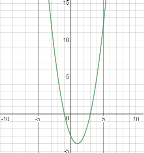
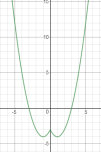
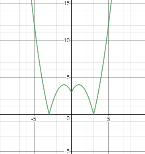
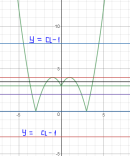
Відповідь: Якщо ,  розв’язків немає;  якщо , або рівняння має два розвʼязки.

Якщо або , рівняння має чотири розвʼязки ; якщо, рівняння має пʼятьрозвʼязків, якщо  рівняння має шість розвʼязків. 

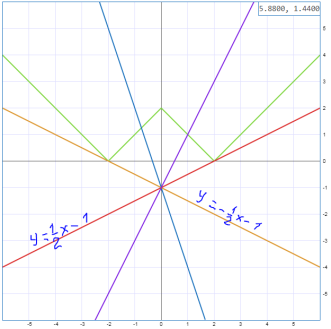
Приклад 2.

При яких значеннях , рівняння має три розв’язки?

Розв’язування

Розв’яжемо рівняння графічним методом. Будуємо графіки функцій   i в одній системі координат:

План побудови

1).		1).
2).
3).		2). : виконуємо паралельне перенесення графіка вздовж осі ОУ на одиниць

Мал. 10

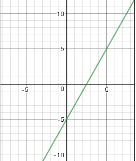
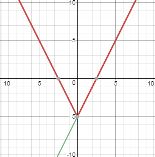
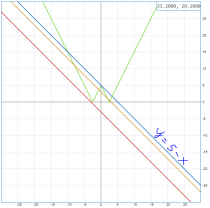
Приклад 3

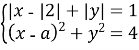
У відповідь запишіть їх суму.

Розв’язання

Розв’яжемо завдання графічним методом:

будуємо графіки рівняння i.

Графік першого рівняння це коло з центром в точці . Графік другого рівняння будуємо за допомогою геометричних перетворень графіків функцій.

План побудови:

1. 
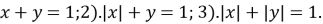
2. Виконаємо йогопаралельне перенесеннявздовж осі ОХ на 12 одиниць праворуч.

Мал.11

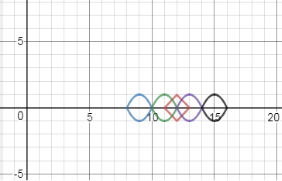
Система має єдиний розв’язок, якщо графіки мають одну спільну точку.

Виконуємо паралельне перенесення кола на одиниць вправо . Маємо чотири випадки:

Відповідь: 48.

Приклад 4

При яких значеннях параметра нерівність

має розв’язки?

Розв’язання

Розв’яжемо дану нерівність графічно:

Побудуємо графіки функцій

Мал.12

 

Маємо відповідь: