Презентація "Аксономентричні проекції"
Про матеріал
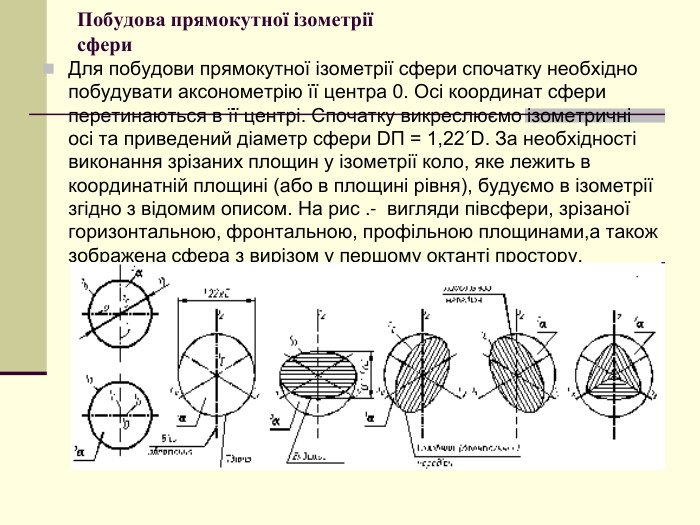
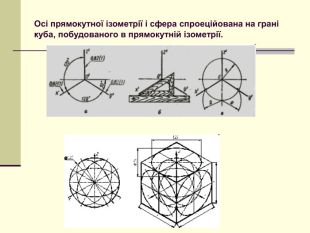
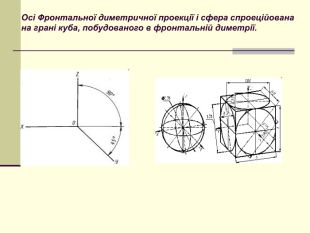
Аксонометри́чні проє́кції (від дав. -гр. ἄξων — «вісь» + μετρέω — «міряю») — наочне зображення просторових форм на площині методом паралельного проєктування.
Яку площину називають площиною аксонометричних проекцій?
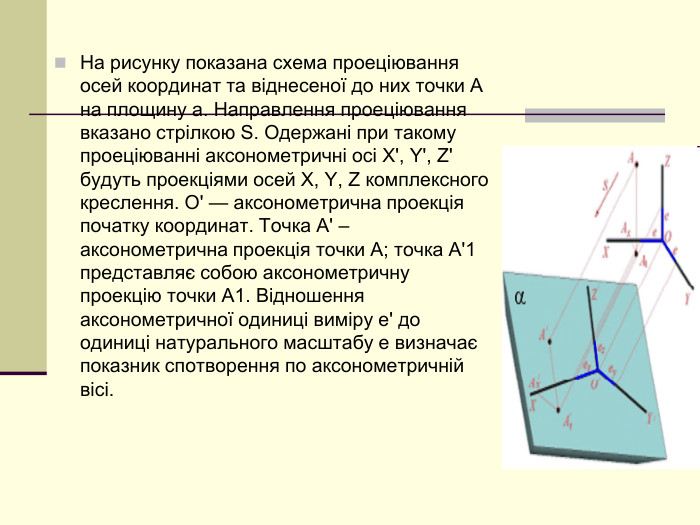
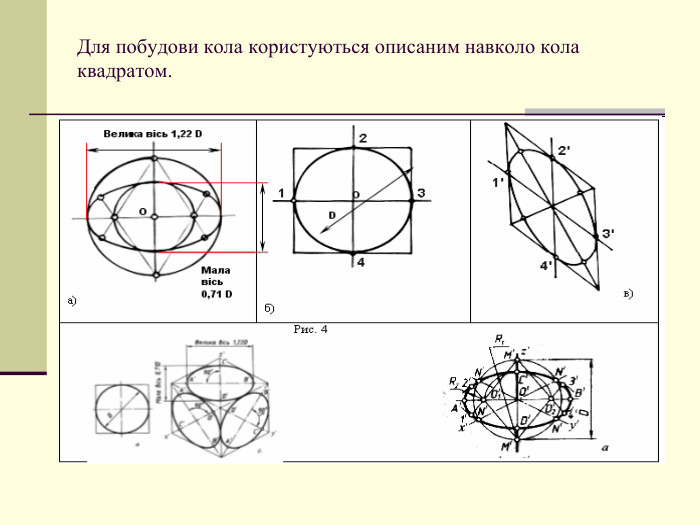
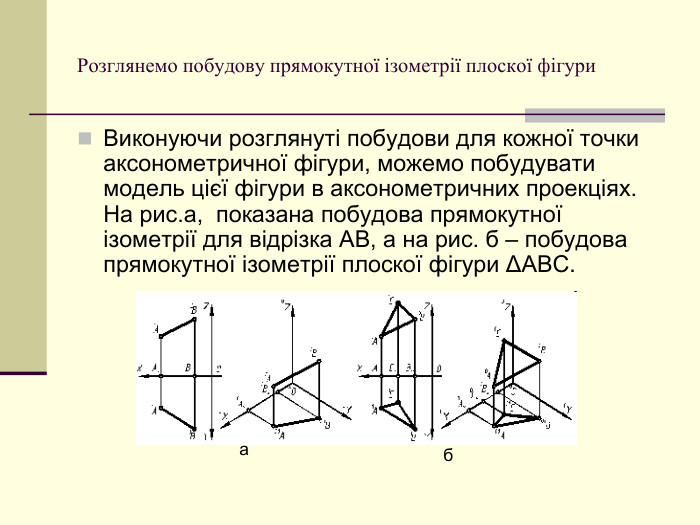
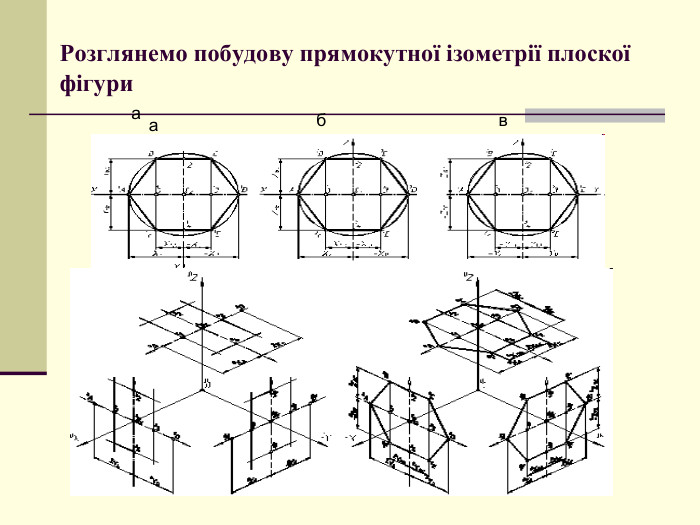
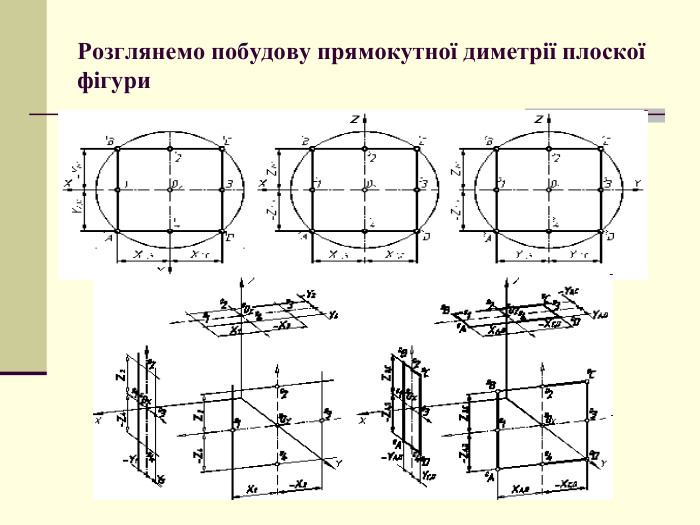
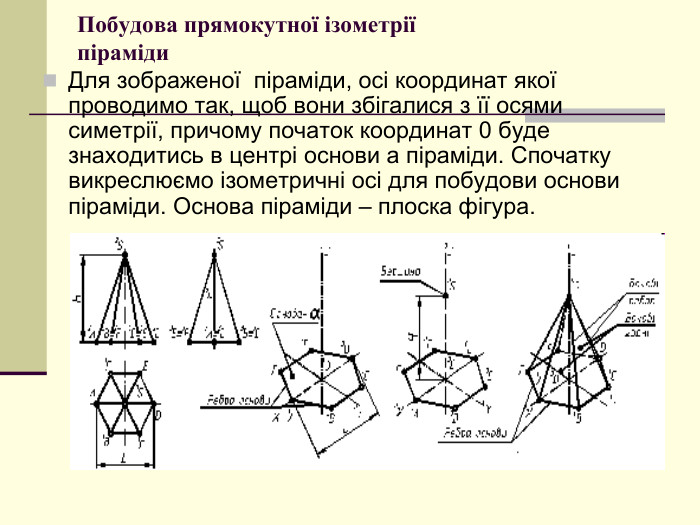
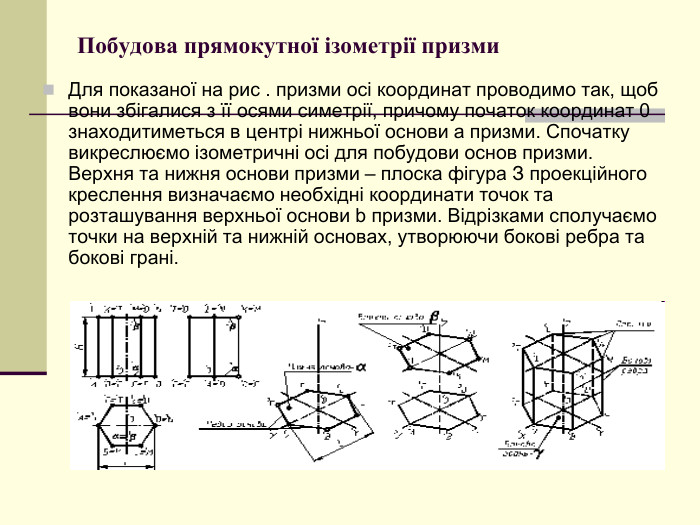
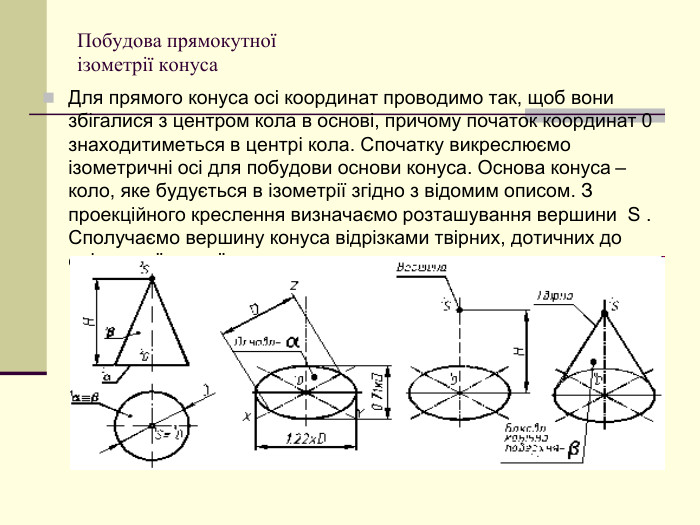
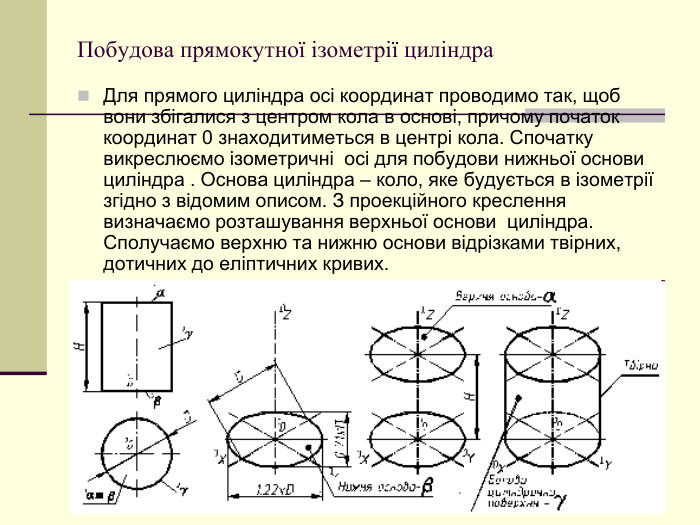
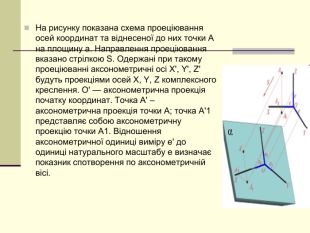
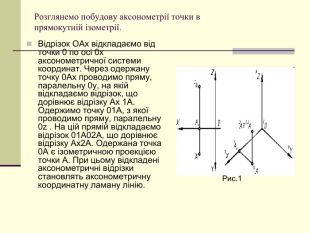
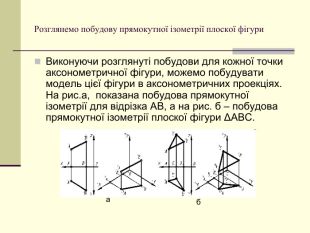
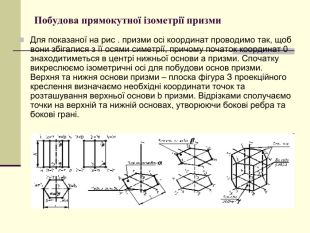
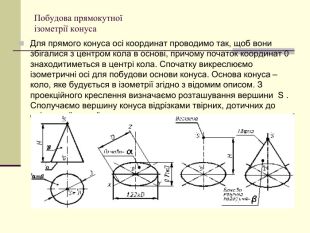
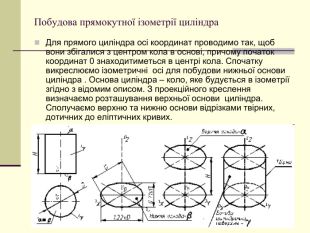
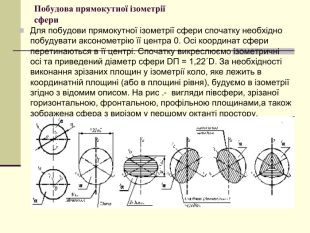
Щоб одержати наочне зображення, предмет певним чином розміщують відносно координатних осей х, у і z і разом з ними проеціюють його на довільну площину. Цю площину називають площиною аксонометричних проекцій, а проекції координатних осей називають аксонометричними осями Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку