Презентація Алгебра 10 клас "Корінь n-го степеня"

Тема уроку: АЛГЕБРАКорінь n-го степеня. Арифметичний корінь n-го степеня. 10 клас

ПРОСМОТР ПРЕЗЕНТАЦІЇ

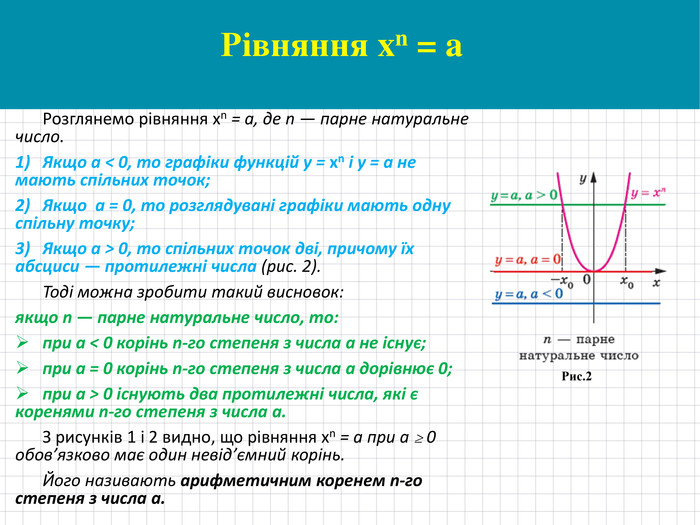
Корінь n-го степеня. Що таке Корінь n-го степеня числа а?Квадратним коренем (коренем другого степеня) з числа a називають таке число, квадрат якого дорівнює a. Аналогічно дають означення кореня n-го степеня з числа a, де n ∈ N, n > 1. Означення. Коренем n-го степеня з числа a, де n ∈ N, n > 1, називають таке число, n-й степінь якого дорівнює a. Наприклад:коренем п’ятого степеня з числа 32 є число 2, оскільки 25 = 32; коренем третього степеня з числа –64 є число –4, оскільки (–4)3 = –64; коренями четвертого степеня з числа 81 є числа 3 і –3, оскільки 34 = 81 і (–3)4 = 81. З означення випливає, що будь-який корінь рівняння xn = a, де n ∈ N, n > 1, є коренем n-го степеня з числа a, і навпаки, корінь n-го степеня з числа a є коренем розглядуваного рівняння.

Корінь n-го степеня, n – непарне. Якщо n — непарне натуральне число, то графіки функцій y = xn і y = a при будь-якому a перетинаються в одній точці (рис. 1). Це означає, що рівняння xn = a має єдиний корінь при будь-якому a. Висновок: якщо n — непарне натуральне число, більше за 1, то корінь n-го степеня з будь-якого числа існує, причому тільки один. Корінь непарного степеня n, n > 1, з числа a позначають так: 𝑛𝑎 (читають: «корінь n-го степеня з a»). Знак 𝑛.. називають знаком кореня n-го степеня або радикалом. Вираз, який стоїть під радикалом, називають підкореневим виразом. Наприклад, Корінь третього степеня також прийнято називати кубічним коренем. Наприклад, запис 32 читають: «корінь кубічний з числа 2».  

До уваги

Арифметичний корінь n-го степеня. Означення. Арифметичним коренем n-го степеня з невід’ємного числа a, де n ∈ N, n > 1, називають таке невід’ємне число, n-й степінь якого дорівнює a. Арифметичний корінь n-го степеня з невід’ємного числа a позначають так: 𝑛𝑎  

Рівняння xn = a. Розглянемо рівняння xn = a, де n — парне натуральне число. Якщо a < 0, то графіки функцій y = xn і y = a не мають спільних точок; Якщо a = 0, то розглядувані графіки мають одну спільну точку; Якщо a > 0, то спільних точок дві, причому їх абсциси — протилежні числа (рис. 2). Тоді можна зробити такий висновок: якщо n — парне натуральне число, то: при a < 0 корінь n-го степеня з числа a не існує; при a = 0 корінь n-го степеня з числа a дорівнює 0; при a > 0 існують два протилежні числа, які є коренями n-го степеня з числа a. З рисунків 1 і 2 видно, що рівняння xn = a при a ≥ 0 обов’язково має один невід’ємний корінь. Його називають арифметичним коренем n-го степеня з числа a.

Систематизуємо дані про розв’язки рівняння у вигляді схеми:

Розв'язати рівняння: Відповідь:

Вла­стивості кореня n-го степеня. Властивість 1 Властивість 2 Властивість 3 Властивість 4 Властивість 5

Розв'язування вправ:1. Знайдіть значення виразів:2. Обчисліть3. Знайдіть корінь із степеня4. Спростіть вирази

Тренувальні вправи по підручнику: Дякую за урок!§ 3. №3.7, 3.10, 3.12, 3.15, 3.20.