Презентація Алгебра 10 клас "Парні та непарні функції"
Про матеріал
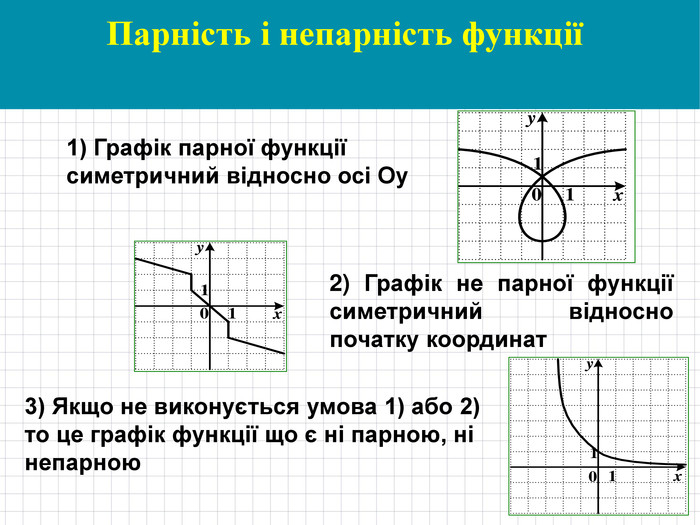
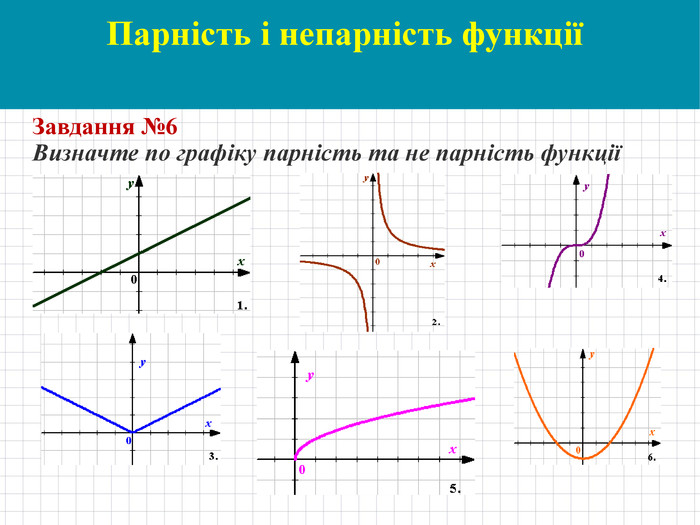
Парні та непарні функції
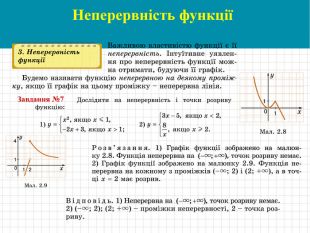
D(f)=R – область визначення
симетрична відносно
початку координат
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



























-

Гадаліна Тетяна Михайлівна
16.10.2023 в 15:56
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Г.С. Шинкаренко
11.10.2023 в 08:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Клепікова Ольга Анатоліївна
25.09.2023 в 22:15
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
21.05.2023 в 17:37
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Якименко Оксана Вікторівна
03.11.2022 в 23:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пустовойт Володимир Іванович
21.09.2022 в 12:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 3 відгука