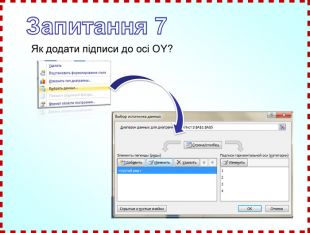
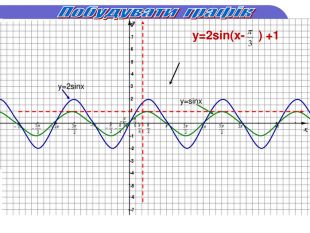
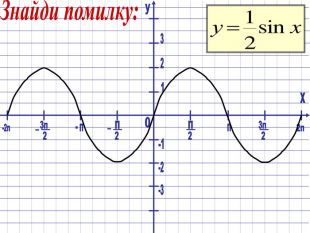
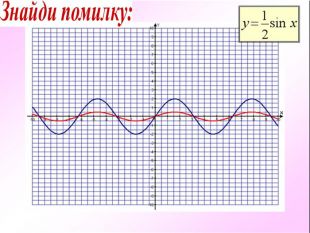
Презентація бінарного заняття з математики та інформатики на тему: «Властивості та графіки тригонометричних функцій. Діаграми і графіки в MS Excel».
Про матеріал
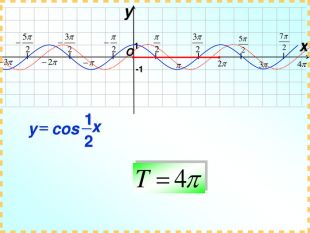
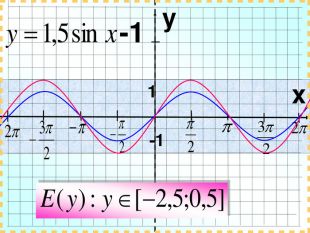
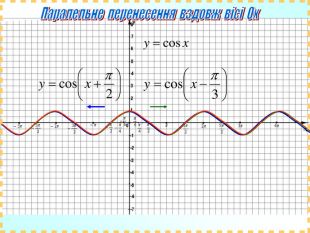
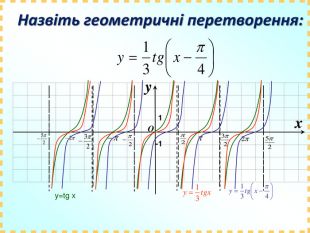
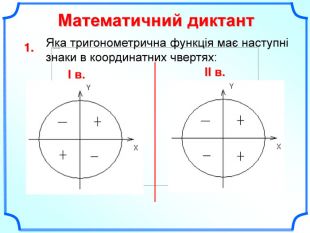
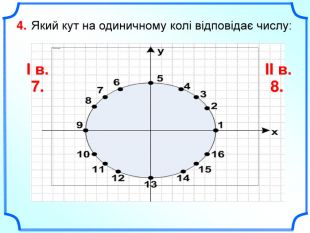
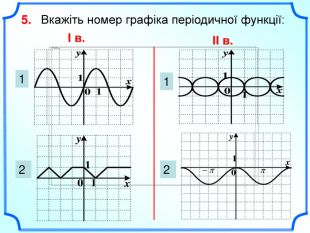
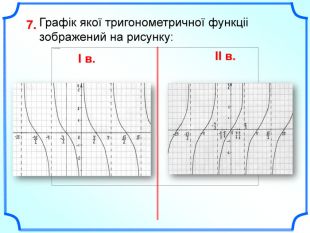
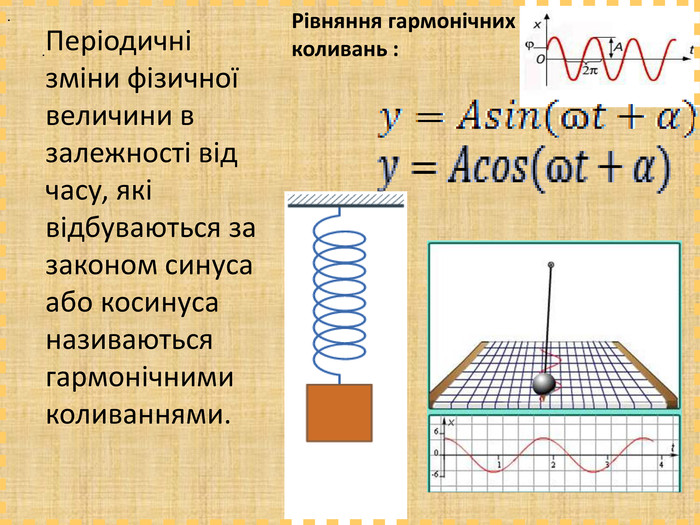
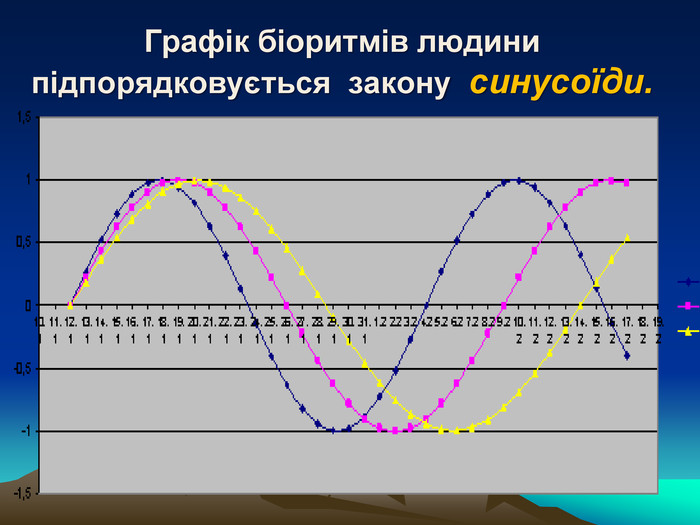
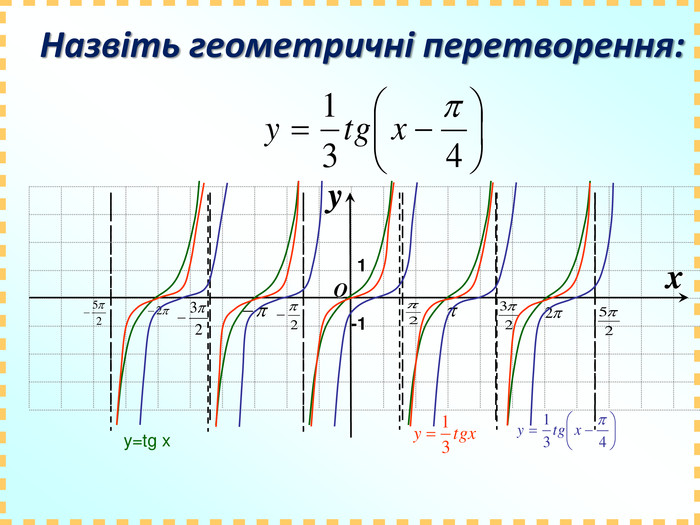
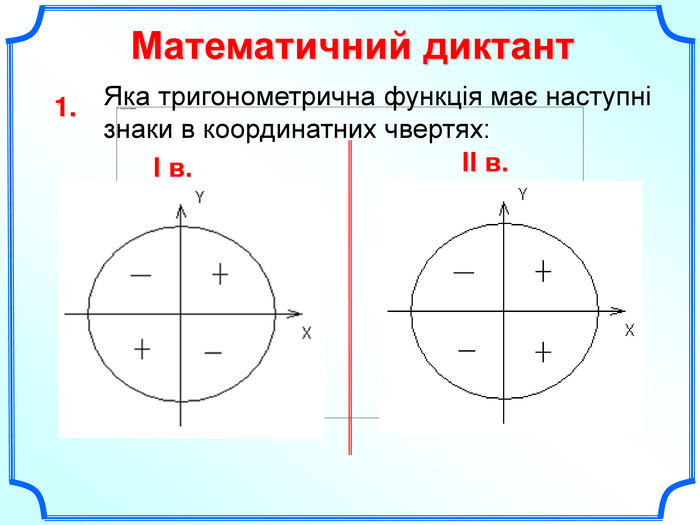
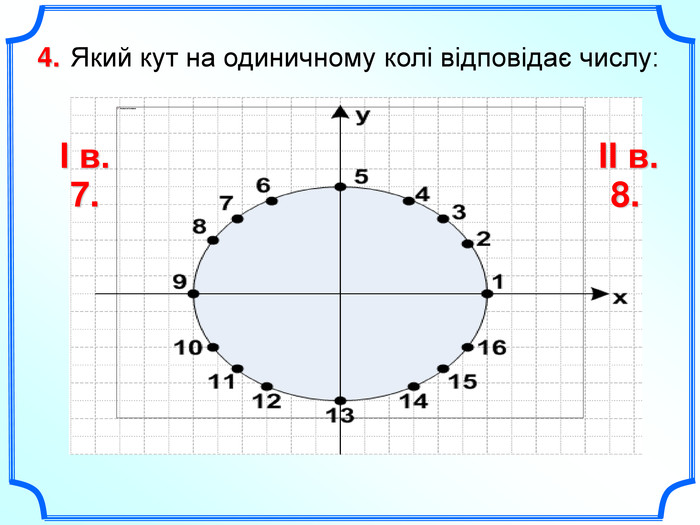
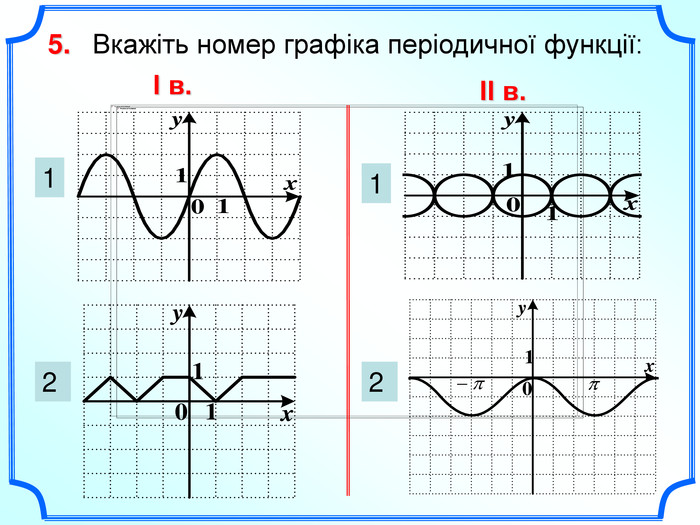
Дане бінарне заняття є заняттям для узагальнення та поглиблення знань, вмінь та навичок, одержаних на заняттях з математики та інформатики. Метою заняття є: закріпити вміння та навички побудови графіків тригонометричних функцій, застосовуючи геометричні перетворення, а також в програмі MS Excel; показати між предметні зв'язки даної області математики з інформатикою, біологією, фізикою; вказати учням на актуальність і вагомість даної теми в інших сферах діяльності; виявити за допомогою побудови графіків в MS Excel можливі перетворення з графіками тригонометричних функцій та зробити висновки; показати важливість знань і умінь у сфері інформаційних комп'ютерних технологій, а саме знань електронної таблиці MS Excel.
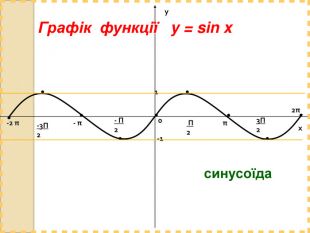
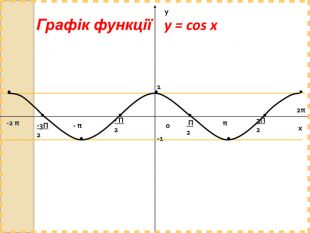
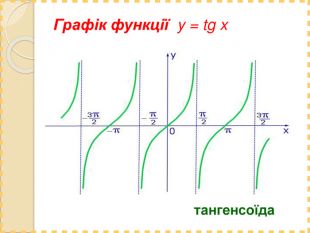
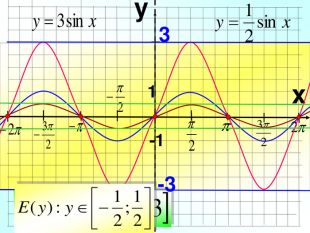
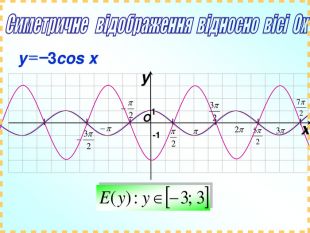
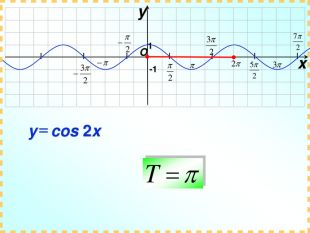
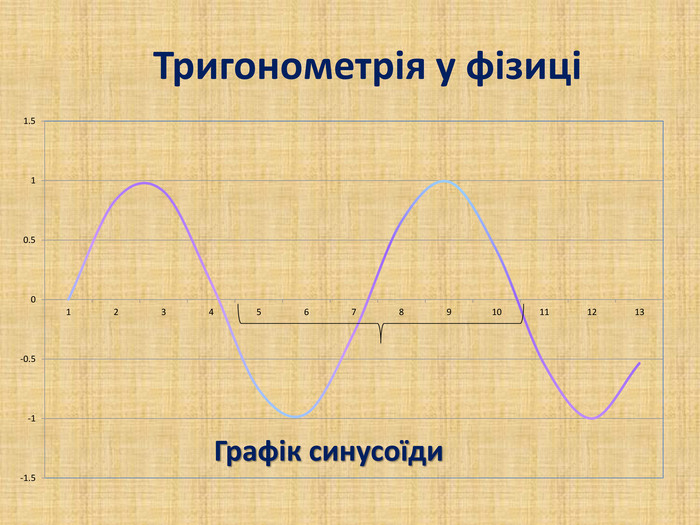
Практично завжди побудова графіків перетворюється в досить трудомісткий процес, особливо якщо це графіки тригонометричних функції. Заняття спрямоване на те, щоб показати як інформаційні технології, зокрема, електронні таблиці MS-Excel дозволяють перетворити цей процес у досить швидкий, доступний і наочний.
Перегляд файлу


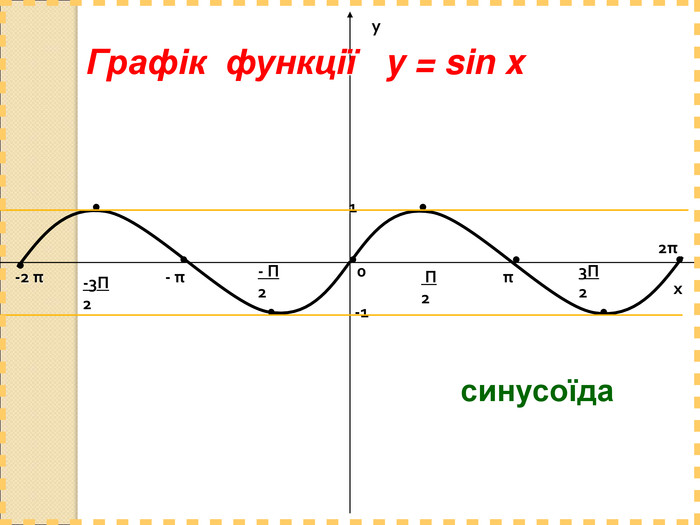

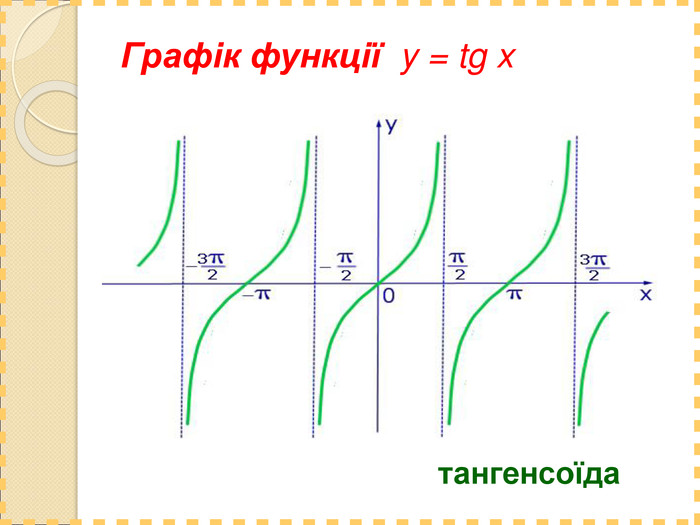


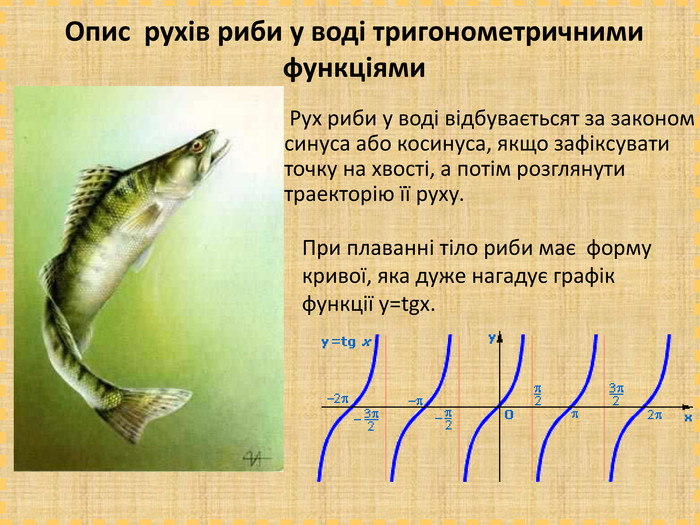















![[adcos(t) + ddt , bdsin(t), cdt + edt2] [adcos(t) + ddt , bdsin(t), cdt + edt2]](/uploads/files/731047/140416/152316_images/29.jpg)


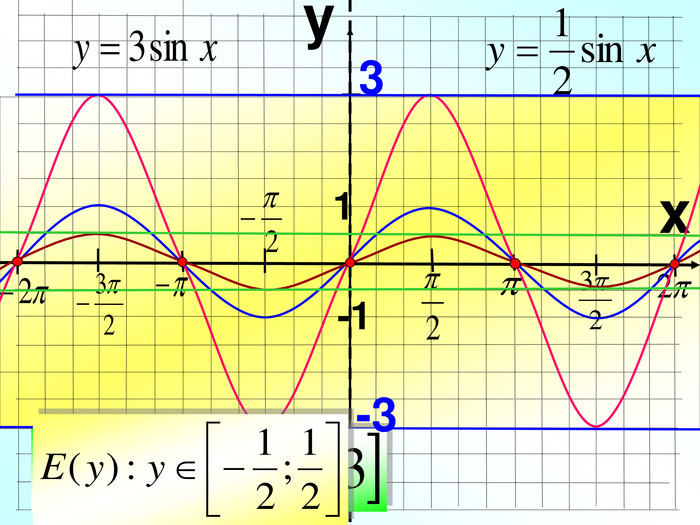


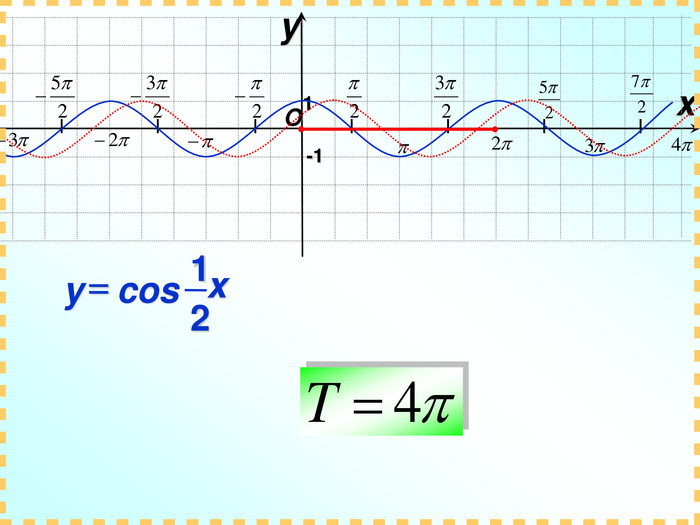
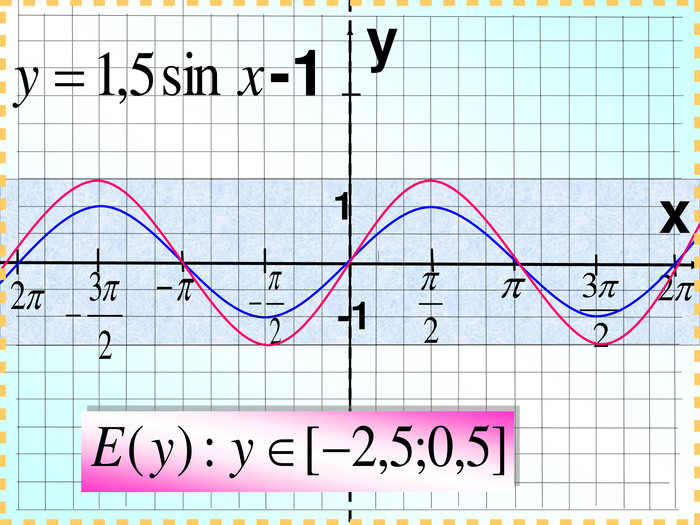
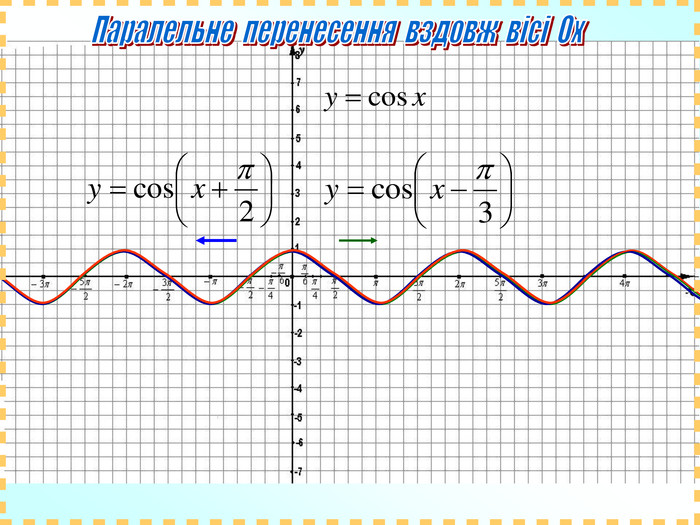




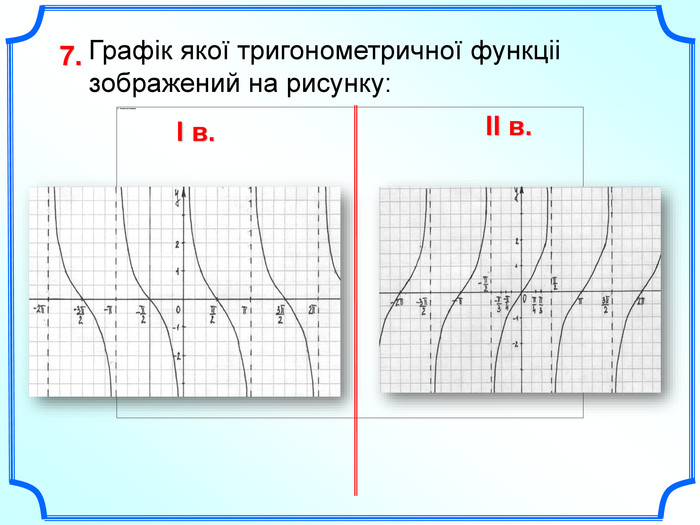

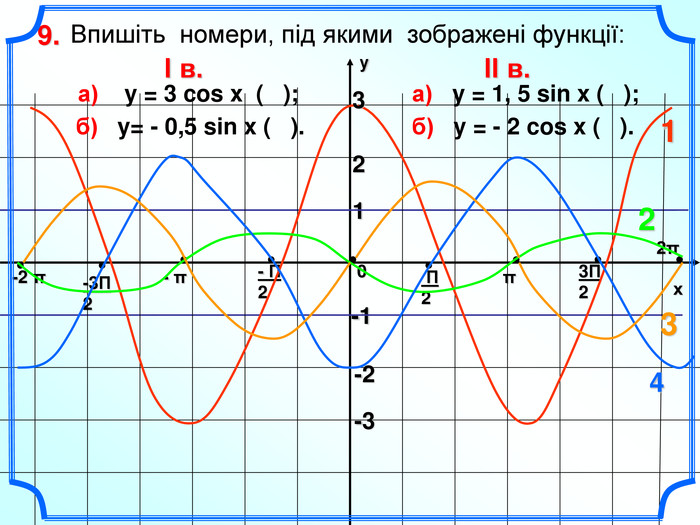


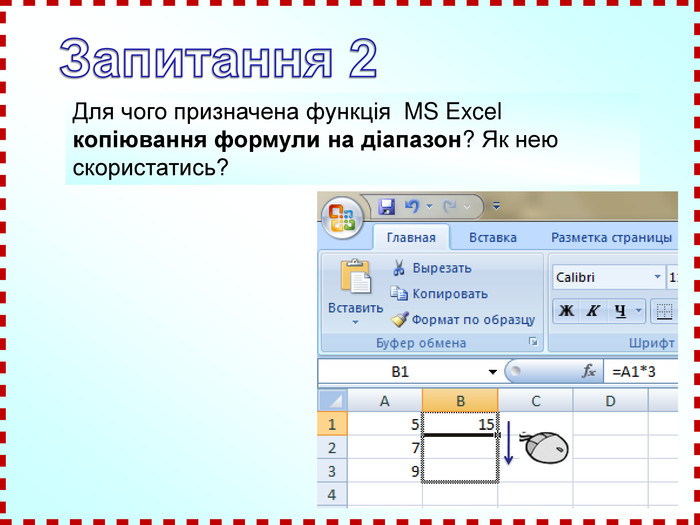

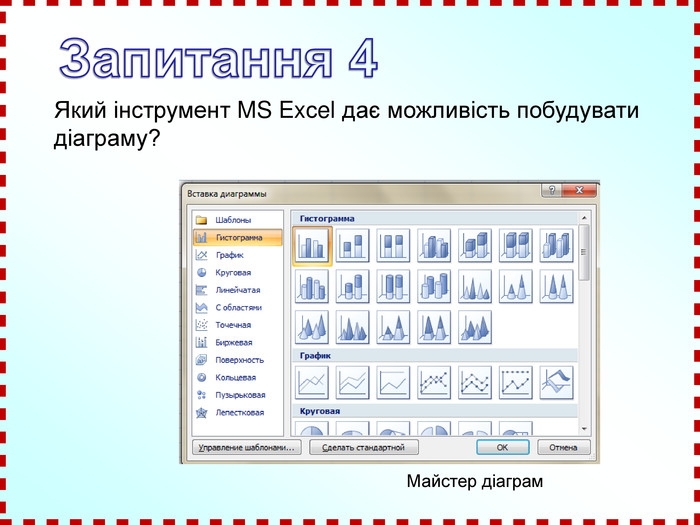















![Домашнє завдання: Побудувати графіки функцій: y = 2tg(x+ )+1; y = 0,5cos x – 1 в зошитах з математики ; та в MS Excel на відрізку [-2 ; 2 ] з кроком . Домашнє завдання: Побудувати графіки функцій: y = 2tg(x+ )+1; y = 0,5cos x – 1 в зошитах з математики ; та в MS Excel на відрізку [-2 ; 2 ] з кроком .](/uploads/files/731047/140416/152316_images/75.jpg)
Зміст слайдів
ppt
Додав(-ла)
Єфімова Олена В'ячеславівна
Додано
19 січня 2020
Переглядів
1287
Оцінка розробки
Відгуки відсутні


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
Рекомендовані матеріали
Схожі матеріали