Посібник для уроків алгебри ІІ семестр 10 класу
Ківерцівська експериментальна школа
Навчальний посібник


___________________________________
___________________________________
Тема №3 Тригонометричні функції
Урок №1
«Не буде ледачий пекти свого полову,
а людина трудяща набуде маєток цінний»
Книга приповістей Соломонових 12 : 27

Тригонометричні функції
Питання
- Радіанне вимірювання кутів. Тригонометричні функції числового аргументу.
- Періодичні функції.
- Графіки тригонометричних функцій.
Література
Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту): Підручник для 10 класу закладів загальної середньої освіти. Київ: Генеза, 2018 рік, §§7 – 9, стор. 68 – 94; §12, стор. 109 – 121.
|
1. Радіанне вимірювання кутів. Тригонометричні функції числового аргументу |
|||
|
1.1 |
Тригонометрія – наука про вимірювання трикутників (з грецької «тригонон» – трикутник, «метріо» – міра) |
||
|
1.2 |
Поняття кута |
||
|
У геометрії |
У тригонометрії |
||
|
Кут – геометрична фігура, утворена двома променями, які виходять з однієї точки
О В
|
Кут – фігура, утворена при повороті променя на площині навколо його початку
|
||
|
1.3 |
Вимірювання кутів |
||
|
Градусна міра кута ( |
|||
|
Кожному куту ставиться у відповідність градусна міра |
Кожному куту як фігурі ставиться у відповідність кут повороту α, за допомогою якого утворений цей кут (поворот проти годинникової стрілки – α > 0; поворот за годинниковою стрілкою – α < 0) |
||
|
Радіанна міра кута |
|||
|
1° = |
|||
|
1.4
|
з центром у початку координат і радіусом 1.
|
||
|
1.5 |
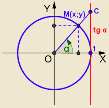
Косинусом кута повороту α називають абсцису x точки М (x; y) одиничного кола, отриманої внаслідок повороту точки
|
|
|
|
1.6 |
Синусом кута повороту α називають ординату y точки М (x; y) одиничного кола, отриманої внаслідок повороту точки
|
||
|
1.7 |
Тангенсом кута повороту α називають відношення синуса цього кута до його косинуса
|
|
|
|
1.8 |
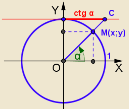
Котангенсом кута повороту α називають відношення косинуса цього кута до його синуса
|
|
|
|
1.9 |
Функції |
||
|
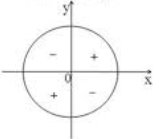
1.10 |
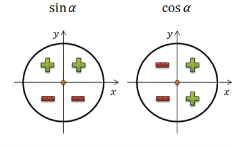
Знаки тригонометричних функцій
|
||
|
1.11 |
Функція косинус є парною, а функції синус, тангенс і котангенс – непарним Всередині косинуса живе панда, а панда голодний. Тому він зїдає знак мінус. Функція косинус – парна. |
||
|
2. Періодичні функції |
|||
|
2.12 |
Функцію |
||
|
2.13 |
Головним періодом функцій
|
||
3. Графіки тригонометричних функцій
- . Графіки тригонометричних функцій
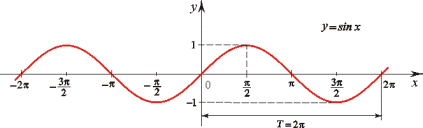
![]()
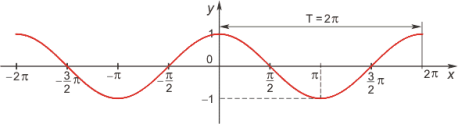
![]()
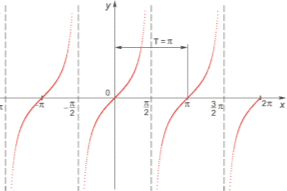
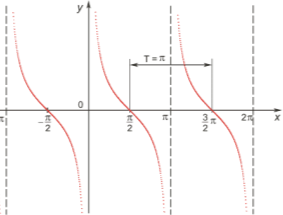
- Таблиця значень тригонометричних функцій деяких кутів
|
α |
0° |
30° |
45° |
60° |
90° |
120° |
135° |
150° |
180° |
270° |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
0 |
|
|
|
1 |
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
1 |
|
– |
|
|
|
0 |
– |
|
|
– |
|
1 |
|
0 |
|
|
|
– |
0 |
Урок №2
«Зібратися разом – це початок,
триматися разом – це процес,
працювати разом – це успіх».
Генрі Діорд
Фронтальне опрацювання матеріалу
Радіанне вимірювання кутів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 1.4 блоку №3.
- Усно дайте відповіді на питання:
- Наука, що в перекладі з грецької означає «Вимірювання трикутника».
- 1/180 частина розгорнутого кута.
- Дуга, довжина якої дорівнює радіусу кола.
- Коло з центром в початку координат і радіусом рівним одиниці.
- Запишіть формули переходу від градусної міри кута до радіанної і навпаки.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Письмово виконайте вправи, стор. 80 – 82 підручника: 8.1, 8.3, 8.16, 8.19, 8.22.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 3.
Самостійно виконайте завдання: накресліть таблицю в зошиті і заповніть її.
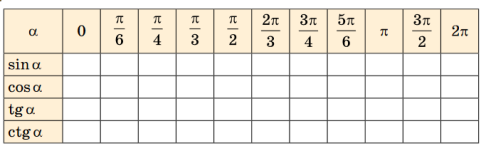
Урок №3
«Зібратися разом – це початок,
триматися разом – це процес,
працювати разом – це успіх».
Генрі Діорд
Фронтальне опрацювання матеріалу
Тригонометричні функції числового аргументу
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 1.9 блоку №3.
- Усно дайте відповіді на питання:
- Що таке тригонометрія?
- Що називають 1º?
- Що називають 1 радіаном?
- Яка різниця між кутом в геометрії та тригонометрії?
- Що таке одиничне коло?
- Запишіть формули переходу від градусної міри кута до радіанної і навпаки.
- Що називають тригонометричними функціями?
- Дати означення тригонометричних функцій.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
- Письмово виконайте вправи, стор. 75, 76 підручника: 7.15, 7.27.
- Письмово виконайте вправи, стор. 81 підручника: 8.14, 8.24, 8.33.
- Знайдіть значення виразу:
-
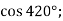
-
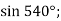
-
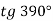 ;
;
-
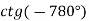 .
.
-
Який знак має:
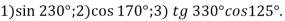
-
Який знак має:
Завдання 3.
Виконати самостійно:
- В які чверті лежать кути?
|
|
|
|
|
|
|
|
|
|
|
|
- Вставити пропущене число:
|
|
|
|
|
|
|
|
? |
-
Обчислити
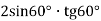 .
.
Уроки №4, 5
«Я можу все в Тім, Хто
мене підкріпляє, – в Ісусі Христі»
Послання ап.. Павла до филипʼян 4:13
Фронтальне опрацювання матеріалу
Властивості і графіки тригонометричних функцій
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть блок № 3.
- Усно дайте відповіді на питання:
- Яка наука називається тригонометрією?
- Дайте визначення кута у тригонометрії.
- 1 радіан – це…
- Що називають одиничним колом?
- Дайте визначення всім тригонометричним функціям.
- Які знаки мають тригонометричні функції у кожній періодичній чверті?
- Розкажіть про парність тригонометричних функцій.
- Які періоди мають тригонометричні функції?
-
Як називаються графіки функцій
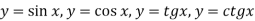 ?
?
- Які перетворення графіків вам відомі?
Завдання 2.
За допомогою презентації, запропонованої вчителем, визначте властивості функцій ![]() .
.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконайте письмово вправи:
-
Знайдіть найменший додатний період функцій: 1)
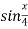 ; 2)
; 2) 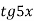 .
.
-
Побудувати графік функції
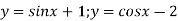 .
.
-
Побудуйте графік функції
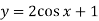 . Вкажіть множину значень та нулі цієї функції.
. Вкажіть множину значень та нулі цієї функції.
Завдання 4.
-
Обчисліть: 1)
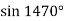 ; 2)
; 2) 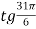 .
.
- Побудувати графік функції y = 0.5cos x + 2.
-
Побудуйте графік функції
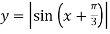
-
Знайдіть найменше значення функції:
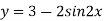 .
.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
- Встановіть відповідність між виразами (1 – 4) та їх значеннями (А – Д).
1 ![]() А – 1 Д
А – 1 Д ![]()
2 ![]() Б 0
Б 0
3 c![]() B 1
B 1
4 ![]() Г значення виразу не визначено
Г значення виразу не визначено
-
Обчисліть
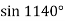 .
.
-
Знайдіть значення виразу
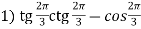 ; 2)
; 2) 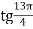 .
.
-
Визначте знак виразу: 1)
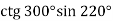 ; 2)
; 2)  .
.
-
Побудуйте графік функції
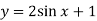 . Вкажіть множину значень та нулі цієї функції.
. Вкажіть множину значень та нулі цієї функції.
Урок №7
«Серце розумне шукає знання,
а уста безумних глупоту пасуть»
Книга приповістей Соломонових 15:14
Внутрішньопредметне узагальнення матеріалу
Тригонометричні функції
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повторіть блок № 3, особливу увагу зверніть на тези 1.1; 1.3 – 1.8; 1.11; 2.12; 2.13 .
- Дайте письмово відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконати вправи:
- Записати у радіанній мірі кут 300°.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Обчислити
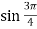 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Вкажіть область значень функції
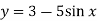 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Завдання 3.
Виконати письмово вправи:
-
Знайти значення виразу
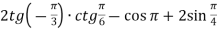 .
.
-
Визначити знак виразу
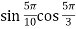 .
.
-
Визначити парність функції
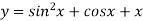 .
.
-
Обчислити найбільше і найменше значення функції
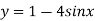 .
.
-
Побудувати графік функції
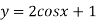 і зазначити область значень функції.
і зазначити область значень функції.
Тема №4. Тригонометричні формули
Урок №1

Тригонометричні формули
«У математиків існує своя мова – це формули»
С.В.Ковалевська
Питання
- Основні співвідношення між тригонометричними функціями одного аргументу.
- Формули зведення.
- Формули додавання.
- Формули подвійного аргументу.
- Формули половинного аргументу.
- Формули суми і різниці тригонометричних функцій.
- Формули перетворення добутку тригонометричних функцій у суму.
- Обернені тригонометричні функції.
- Найпростіші тригонометричні рівняння
Література
Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту): Підручник для 10 класу закладів загальної середньої освіти. Київ: Генеза, 2018 рік, §§10, 11, стор. 94 – 109; §§13 – 16, стор. 121 – 158.
|
1. Основні співвідношення між тригонометричними функціями одного аргументу |
|||||||||||||
|
1.1 |
4) |
||||||||||||
|
2. Формули зведення |
|||||||||||||
|
2.2 |
Формулами зведення називають формули, за допомогою яких тригонометричні функції від аргументів виду |
||||||||||||
|
2.3 |
Правила для запису формул зведення
|
||||||||||||
|
3. Формули додавання |
|||||||||||||
|
3.4 |
|
||||||||||||
|
4. Формули подвійного аргументу |
|||||||||||||
|
4.5 |
2)
|
||||||||||||
|
5. Формули половинного аргументу |
|||||||||||||
|
5.6 |
|
||||||||||||
|
6. Формули суми і різниці тригонометричних функцій |
|||||||||||||
|
6.7 |
|
||||||||||||
|
7. Формули перетворення добутку тригонометричних функцій у суму |
|||||||||||||
|
7.8 |
3) |
||||||||||||
|
8. Обернені тригонометричні функції |
|||||||||||||
|
8.9 |
Арккосинусом числа b, де
arсcos b = α, якщо |
|
|||||||||||
|
8.10 |
Арксинусом числа b, де
arcsin b = α, якщо |
|
|||||||||||
|
8.11 |
Арктангенсом числа b називають таке число α з проміжку
arctg b = α, якщо |
|
|||||||||||
|
8.12 |
Арккотангенсом числа b називають таке число α з проміжку
arcctg b = α, якщо |
|
|||||||||||
|
8.13 |
Деякі властивості обернених тригонометричних функцій |
||||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||
|
|
|
||||||||||||
|
9. Найпростіші тригонометричні рівняння |
|||||||||||||
|
9.14 |
Рівняння виду
|
|
|||||||||||
|
9.15 |
Розв’язування найпростіших тригонометричних рівнянь |
||||||||||||
|
9.15.1
|
|
||||||||||||
|
9.15.2
|
|
||||||||||||
|
9.15.3 |
|
||||||||||||
Урок №2
«Знання лише тоді знання, коли воно отримане
зусиллям розуму, а не пам’яті»
Л.М.Толстой
Фронтальне опрацювання матеріалу
Основні співвідношення між тригонометричними функціями одного аргументу
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 2.3 блоку №4
- Наука, що в перекладі з грецької означає «Вимірювання трикутника»
- 1/180 частина розгорнутого кута.
- Дуга, довжина якої дорівнює радіусу дуги.
- Як називається коло з центром в початку координат і радіусом один?
- Ордината точки Рα одиничного кола
- Абсциса точки Рα одиничного кола.
- Відношення синуса числа до косинуса цього числа.
- Відношення косинуса числа до його синуса.
- Продовжте формули:
![]()
![]()
5) ![]()
Завдання 2.
Встановити відповідність між тригонометричними виразами
|
|
А) |
|
|
|
|
3) |
|
|
4) |
Г) |
|
5) |
|
|
6) |
Е) |
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
3.1. Спростити вираз ![]() .
.
3.2. Знайдіть значення тригонометричних функцій аргументу ![]() , якщо
, якщо ![]()
3.3. Спростіть вираз:
а) ![]() ;
;
б) ![]() .
.
3.4. Доведіть тотожність: ![]() .
.
Домашнє завдання: підготуйте 3 твердження, пов’язані з нашим блоком, два з них правдиві, а одне – брехня. На уроці потрібно буде озвучити ці твердження, а ваші однокласники повинні вгадати правда це чи брехня.
Урок №3
«Алгебра і геометрія — єдині
країни, де панують тиша й мир»
Марія Аньєзі, італійський математик
Фронтальне опрацювання матеріалу
Формули зведення
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 2.3 блоку № 4.
- Дайте відповіді на питання:
- Які формули називаються формулами зведення?
- Розкажіть схему застосування формул зведення.
- Встановіть відповідність між заданими виразами (1 – 4) та виразами, що їм тотожно дорівнюють (А – Д).
1 ![]() A
A ![]()
2 ![]() Б
Б ![]()
3 ![]() B
B ![]()
4 ![]() Г
Г ![]()
Д ![]()
Завдання 2.
- Знайдіть і виправте, де необхідно, помилки:
![]()
![]() 1) y 2) у 3) у
1) y 2) у 3) у
– + + + – +
![]()
![]() 0 х 0 х 0 х
0 х 0 х 0 х
– + – – – –
![]()
![]()
![]()
- Визначити знак виразів:
- tg 170º; 2) cos 200º; 3) ctg 185º; 4) sin 240º.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Розгляньте приклади 1 – 3, стор. 103 – 104 підручника.
- Користуючись розглянутими прикладами, письмово виконайте вправи, стор. 105 – 107 підручника: 11.3 (1, 3, 5, 7), 11.5 (2, 4, 6, 8), 11.15, 11.17, 11.19.
Урок №4
Найвище призначення математики – знаходити
порядок у хаосі, який нас оточує.
Н. Вінтер (американський математик)
Фронтальне опрацювання матеріалу
Формули додавання
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 3.4 блоку №4.
- Дайте відповіді на питання:
- Повторення значень тригонометричних функцій (усно, колективно):
1. sin 450 = 4. cos 450 = 7. cos 750 =
2. cos 300 = 5. tg 300 =
3. tg 600 = 6. sin 600 =
- Які функції називаються періодичними? Чому дорівнює період функцій у = sin х; у = cos х; у = tg х; у = сtg х?
- Які з тригонометричних функцій є парними, а які непарними?
- Дописати тотожності:
![]()
![]()
- Дайте означення cos α і sin α для одиничного кола.
-
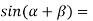
-
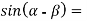
-
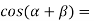
-
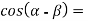
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
2.1. Обчисліть:
![]() 4
4![]()
2) tg 150
3) tg 750
2.2. Знайти значення виразів
1) sin 200 cos 400 + cos 200 sin 400
2) cos 700cos 100 + sin 700 sin 100
![]()
- Обчислити:
1) sin 210 cos 90 + cos 210 sin 90 ; 3) ![]() ;
;
2) sin 800 cos 200 – cos 800 sin 200 ; 4![]()
2.4. Доведіть тотожність
sin (α + β) - sin (α - β) = 2 cos α sin β
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Застосуйте формули зведення та спростіть вираз:
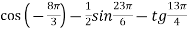 .
.
-
Знайти
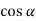 , якщо
, якщо 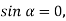 ;
; 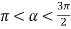 .
.
-
Обчисліть значення всіх тригонометричних функцій кута
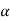 , якщо
, якщо 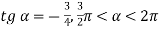 .
.
Урок №6
«Працьовитість – душа
будь-якої справи і запорука добробуту»
Чарльз Діккенс
Фронтальне опрацювання матеріалу
Формули подвійного аргументу
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 5.6 блоку № 4.
- Дайте відповіді на питання:
- Записати основні співвідношення між тригонометричними функціями одного аргументу.
- Що називають формулами зведення?
- Сформулювати правило для запису формул зведення.
- Записати формули додавання.
- Записати формули подвійного аргументу.
- Записати формули половинного аргументу.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Користуючись розглянутими прикладами, виконайте вправи, стор. 133 – 136 підручника: 14.3 (1; 3; 5); 14.7 (2; 4; 6); 14.9; 14.23 (1, 3, 5).
Завдання 3.
 Виконавши вправи, ви дізнаєтесь, який хімічний елемент дуже необхідний людям, і його багато у повітрі Карпат.
Виконавши вправи, ви дізнаєтесь, який хімічний елемент дуже необхідний людям, і його багато у повітрі Карпат.
3.1. ![]() (аргумент – номер букви алфавіту).
(аргумент – номер букви алфавіту).
3.2. Обчислити: 18,5 +2 sin15°·cos15° (номер букви алфавіту).
3.3. Знайти значення виразу: 6![]() (
(![]() –
– ![]() ) (номер букви алфавіту).
) (номер букви алфавіту).
Урок №7
«Більше думай і тоді вирішуй»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Формули суми і різниці тригонометричних функцій
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 6.7 блоку № 4.
- Продовжте формули:
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Усно виконайте вправи:
-
Перетворіть у добуток:
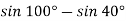 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Обчисліть:
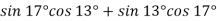 .
.
|
А |
Б |
В |
Г |
|
|
|
1 |
|
Завдання 3.
3.1. Перетворіть на добуток:
1) ![]()
2) ![]()
3) ![]() ;
;
4) ![]() .
.
- Знайдіть значення виразу:
1) ![]()
2) ![]() ;
;
- Доведіть тотожність:
1) ![]() ;
;
2) ![]() .
.
- Виконайте вправи, стор. 141 – 143 підручника: 15.3 (1, 3); 15.17, 15.26 (1, 3).
Урок №8
«Математика – дивовижна вчителька в
мистецтві спрямовувати думки, де вони невпорядковані, і
викорчовувати безглуздя, фільтрувати брудне і наводити ясність»
Жорж Фавр, засновник Мануфактури Zenith
з виробництва годинників, Швейцарія
Фронтальне опрацювання матеріалу
Обернені тригонометричні функції
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 8.9 – 8.13 блоку № 4.
- Усно дайте відповіді на питання:
- Які функції відносяться до обернених тригонометричних функцій?
- Дати означення arccos x, arcsin x, arctg x, arcctg x?
- Які властивості притаманні цим функціям?
Завдання 2.
Накресліть таблицю і заповніть її:
|
а |
–1 |
– |
– |
– |
0 |
|
|
|
1 |
|
arccos а |
|
|
|
|
|
|
|
|
|
|
arcsin а |
|
|
|
|
|
|
|
|
|
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконати вправи:
3.1. Перевірити чи є правильною рівність?
![]() ;
;
2) arcsin ![]() ∙ arcsin
∙ arcsin ![]() =
= ![]() ;
;
3) arccos2 (–![]() ) =
) = ![]() .
.
3.2. Обчислити:
1) arccos ![]() ∙ arccos (–
∙ arccos (–![]() ); 2) arcsin
); 2) arcsin ![]() + arcsin (–
+ arcsin (–![]() ); 3) arcsin 0 + arcsin
); 3) arcsin 0 + arcsin ![]() .
.
3.3. Обчислити:
1) sin (arсcos ![]() ); 2) sin (2 arсcos (–
); 2) sin (2 arсcos (–![]() ).
).
3.4. Обчислити:
1) cos (arcsin ![]() ); 2) cos (2 arccos
); 2) cos (2 arccos ![]() ).
).
3.5. Обчислити:
1) arccos (cos ![]() ); 2) arcsin (sin 4); 3) arcsin (sin 1,2); 4) arccos (cos 5).
); 2) arcsin (sin 4); 3) arcsin (sin 1,2); 4) arccos (cos 5).
3.6. Обчислити 1) sin (arсcos ![]() ); 2) cos (arсsin
); 2) cos (arсsin ![]() ).
).
Урок №9
«Хто зневажає досягнення математики, той завдає
шкоди всій науці, бо той, хто не знає математики, не
може вивчати інші точні науки й не може пізнати світ»
Роджер Бекон, англійський філософ, учений, викладач
Фронтальне опрацювання матеріалу
Найпростіші тригонометричні рівняння
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 8.9 – 9.15 блоку № 4.
- Усно дайте відповіді на питання:
- Рівняння яких видів називаються найпростішими тригонометричними рівняннями?
-
Як розв’язати рівняння виду
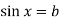 ?
?
-
Як розв’язати рівняння виду
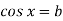 ?
?
-
Як розв’язати рівняння виду
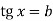 ?
?
-
Як розв’язати рівняння виду
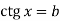 ?
?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Письмово виконати вправи, стор. 155 – 156 підручника: 16.9 (1, 3, 5), 16.13 (2, 4), 16.15, 16.19.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Обчислити: 1)
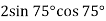 ; 2)
; 2) 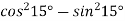 .
.
-
Спростити вираз:
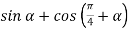 .
.
-
Дано
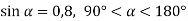 . Знайти
. Знайти 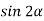 .
.
-
Спростити вираз:
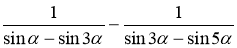
-
Доведіть тотожність:
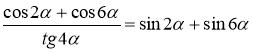
Урок №11
«Освіта — скарб; праця — ключ до нього»
П’єр Буаст, французький лексикограф і поет.
Внутрішньопредметне узагальнення матеріалу
Тригонометричні формули
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повторіть блок № 4.
- Дайте письмово відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконати вправи:
-
Вкажіть розв’язок рівняння:
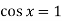 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Знайдіть значення виразу
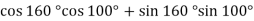 .
.
|
А |
Б |
В |
Г |
|
1 |
0 |
– 1 |
0,5 |
-
Знайдіть значення виразу
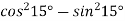 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконати вправи:
-
Знайдіть значення виразу:
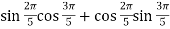 .
.
-
Подайте у вигляді добутку тригонометричних функцій вираз:
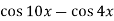 .
.
-
Відомо,що
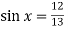 ,
, 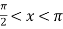 . Знайдіть
. Знайдіть 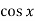 .
.
-
Спростіть вираз
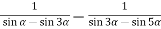 та обчисліть його значення , якщо
та обчисліть його значення , якщо 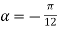 .
.
-
Доведіть тотожність
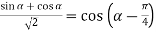 .
.
Тема №5. Похідна
Урок №1

Похідна
«Яка наука може бути благороднішою,
прекраснішою, кориснішою для людини, ніж математика?»
Б. Франклін
Питання
- Геометричний та фізичний зміст похідної.
- Таблиця похідних.
- Правила обчислення похідних. Похідна складеної функції.
Література
Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту): Підручник для 10 класу закладів загальної середньої освіти. Київ: Генеза, 2018 рік, §§17 – 20 , стор. 160 – 190.
|
1. Геометричний та фізичний зміст похідної. Рівняння дотичної до графіка функції |
||||
|
1.1 |
Число
Позначення: |
Для функції
Число 3 – аргумент функції для границі - 2. |
||
|
1.2 |
Границя функції f у точці |
|||
|
1.3 |
Якщо |
|||
|
1.4 |
Різницю |
|||
|
1.5 |
Похідною функції |
|||
|
1.6 |
Функцію, яка має похідну в точці |
|||
|
1.7 |
Механічний зміст похідної: похідна – це миттєва швидкість руху матеріальної точки у момент часу |
|||
|
1.8 |
Геометричний зміст похідної: похідна – це кутовий коефіцієнт дотичної до графіка функції |
|||
|
2. Таблиця похідних |
||||
|
2.9 |
2)
3)
4)
5) |
6)
7)
8)
9)
10) |
||
|
3. Правила обчислення похідних. Похідна складеної функції. |
||||
|
3.10 |
Похідна суми диференційованих функцій дорівнює сумі похідних цих функцій |
|
||
|
3.11 |
Похідна добутку диференційованих функцій дорівнює сумі добутків похідної першої функції на другу та першої функції на похідну другої |
|
||
|
3.12 |
Сталий множник можна виносити за знак похідної |
|
||
|
3.13 |
Похідна частки диференційованих функцій дорівнює дробу, чисельник якого є різницею добутків похідної першої функції на другу та першої функції на похідну другої, а знаменник дорівнює квадрату другої функції |
|
||
Урок №2
«Наука складається з фактів, як будинок з каменів, але набір
фактів ще не наука, так само як купа каміння ще не будинок»
Анрі Пуанкаре, французький математик, фізик, філософ
Фронтальне опрацювання матеріалу
Задачі, що приводять до поняття похідної. Фізичний і геометричний зміст похідної
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 1.8 блоку № 5.
-
Усно дайте відповіді на питання:
- Сформулюйте означення границі функції у точці.
- Що називають приростом аргументу функції?
- Що називають приростом функції?
- Сформулюйте означення похідної функції в даній точці.
- В чому полягає геометричний зміст похідної?
- В чому полягає фізичний зміст похідної?
- Яка функція називається диференційованою?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Розгляньте приклад розв’язування вправи:
Тіло масою 2 кг рухається прямолінійно за законом ![]() , s(t) вимірюється в сантиметрах, час t – в секундах. Знайти діючу силу. Тіло рухається 2с.
, s(t) вимірюється в сантиметрах, час t – в секундах. Знайти діючу силу. Тіло рухається 2с.
Розв’язання
![]()
При t = 2c, ![]()
![]() ,
, ![]()
![]()
Завдання 3.
Користуючись розглянутим прикладом, письмово виконайте вправи:
- Точка рухається за законом s (t) = 6 - 4t +12 (м). У який момент часу швидкість руху точки дорівнює 10 м/с? (ЗНО 218)
|
А |
Б |
В |
Г |
Д |
|
2с |
3с |
5с |
6с |
7с |
-
Знайти миттєву швидкість руху точки у момент часу t = 2c, якщо вона рухається по прямій згідно закону
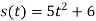 .
.
- Дотична до графіка функції y = f(x) у точці з абсцисою х0 утворює з додатним напрямом осі ОХ кут 45°. Знайдіть f'(х0) (ЗНО 2018).
-
Закон руху матеріальної точки по прямій задано формулою
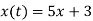 , де
, де 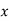 – координата точки в момент часу
– координата точки в момент часу 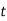 . Знайдіть миттєву швидкість руху точки при
. Знайдіть миттєву швидкість руху точки при 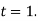
-
Тіло рухається прямолінійно за законом
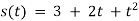 (м). Визначте його швидкість і прискорення в момент часу t = 3 с.
(м). Визначте його швидкість і прискорення в момент часу t = 3 с.
-
Знайдіть приріст функції
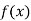 у точці
у точці 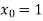 , якщо
, якщо 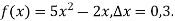
-
Знайдіть приріст функції
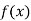 у точці
у точці 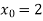 , якщо
, якщо 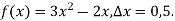
-
Знайдіть кутовий коефіцієнт дотичної до графіка функції
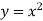 в точці
в точці 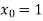 .
.
-
Знайдіть кутовий коефіцієнт дотичної до графіка функції
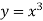 в точці
в точці 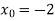 .
.
Урок №3
«Ми не можемо заборонити птахам пролітати над нашою головою, але
ми не дозволяємо їм сідати нам на голову і вити на ній свої гнізда. Подібно
до цього ми не можемо заборонити поганим думкам інколи приходити
до нас в голову, але ми повинні не дозволяти їм гніздитися в нашому мозку»
Мартін Лютер, ініціатор руху в Церкві, пізніше названого Реформацією
Фронтальне опрацювання матеріалу
Похідні елементарних функцій. Похідні суми, добутку і частки функцій
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть блок № 5.
- Усно дайте відповіді на питання:
- Дайте визначення границі функції в точці.
- Дайте визначення похідної в точці.
- Які функції називають диференційованими?
- В чому полягає фізичний і геометричний зміст похідної?
- Сформулюйте правила знаходження похідної суми, добутку і частки.
- Встановіть відповідність
А) ![]()
![]()
![]()
![]()
![]()
![]()
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Розгляньте приклад розв’язування вправи:
Знайдіть похідну функції: у =х ·sinx
Розв’язання
у’ = (x sin x)’ = x’ sinx +x (sin x)’ = 1 · sin x +x cos x = sinx +x cosx
Завдання 3.
Користуючись розглянутим прикладом, письмово виконати вправи:
- Знайдіть похідну функцій:
-
у = 3х2 - 5х + 6; 2) у = -2х3 + 3cosx; 3) y=5x2+
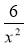 +3ctgx; 4) y=3x·x2+9
+3ctgx; 4) y=3x·x2+9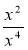 .
.
- Знайдіть похідні функцій:
1) у =![]() sinx;2) у =x2cosx; 3) у = x2
sinx;2) у =x2cosx; 3) у = x2![]() .
.
- Знайдіть похідні функцій:
1) (x - 2)2·x3; 2) (x2 - х)(х3 + x).
- Знайдіть похідні функцій:
![]()
![]()
![]()
![]()
Урок №4
«Не спішіть судити інших, а краще почніть з себе»
Фронтальне опрацювання матеріалу
Правила обчислення похідних
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 2.9 блоку № 5.
- Усно дайте відповіді на питання:
- Дайте визначення границі функції в точці.
- Дайте визначення похідної в точці.
- Які функції називають диференційованими?
- В чому полягає фізичний і геометричний зміст похідної?
-
Сформулюйте правила знаходження похідної суми, добутку і частки.
- Пограти в гру «Навіщо». Дайте відповідь на питання: «Навіщо шкарпетка на математиці?»
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Письмово виконати вправи:
- Знайти похідну функції:
-
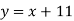 ; 4)
; 4) 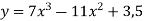 ;
;
-
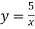 ; 5)
; 5) 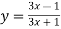 .
.
-
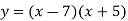 ;
;
-
Обчислити значення похідної в точці
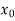 , якщо:
, якщо:
-
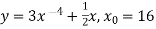 ;
;
-
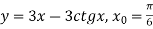 .
.
Завдання 3.
Письмово виконати вправи:
- Знайти похідну функції:
-
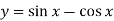 ; 3)
; 3) 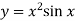 ;
;
-
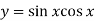 ;
;
-
Розв’язати рівняння
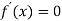 , де
, де 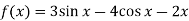 .
.
-
Розв’язати рівняння
Завдання 4.
Письмово виконати вправи:
- Обчислити похідну функції:
-
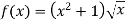 ;
;
-
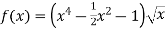 ;
;
-
Обчислити кутовий коефіцієнт дотичної до графіка функції
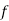 в точці з абсцисою
в точці з абсцисою 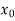 , якщо:
, якщо:
-
Обчислити кутовий коефіцієнт дотичної до графіка функції
-
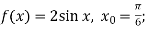
-
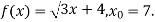
- Визначити, через скільки секунд після початку руху тіло зупиниться, якщо воно рухається за законом:
-
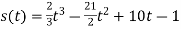 ;
;
-
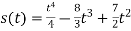 .
.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Обчисліть
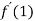 , якщо
, якщо 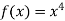 .
.
-
Запишіть кутовий коефіцієнт дотичної до графіка функції
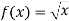 у точці
у точці 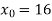 .
.
-
Задано рівняння руху точки
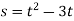 , де s – шлях у метрах, t – час у секундах. Вивести формулу, що виражає швидкість руху в момент часу
, де s – шлях у метрах, t – час у секундах. Вивести формулу, що виражає швидкість руху в момент часу 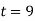 сек.
сек.
-
Знайдіть похідну функції: 1)
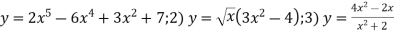 .
.
- Що більше:
-
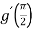 чи
чи 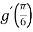 якщо
якщо  ;
;
-
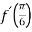 чи
чи 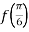 якщо
якщо 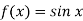 ?
?
-
Розв’язати рівняння:
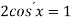 .
.
Урок №6
«І як бажаєте, щоб вам люди
чинили, так само чиніть їм і ви»
Євангелія від Луки 6:31
Внутрішньопредметне узагальнення матеріалу
Похідна
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 5.
- Письмово відповісти на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно розв’язати вправи:
-
Знайдіть похідну функції
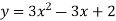 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Знайдіть похідну функції
 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
1 |
-
Обчислити похідну функції: у =
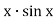
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово розв’язати вправи:
-
Тіло рухається прямолінійно за законом
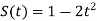 (S – шлях у метрах, t – час у секундах). Обчисліть швидкість руху точки в момент
(S – шлях у метрах, t – час у секундах). Обчисліть швидкість руху точки в момент 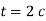 .
.
-
Знайдіть кутовий коефіцієнт параболи
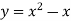 в точці з абсцисою
в точці з абсцисою 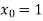 .
.
- Встановити відповідність між функцією та її похідною:
|
1. |
А. Дорівнює: |
|
2. |
Б. Дорівнює: |
|
3. |
В. Дорівнює: |
|
4. |
Г. Дорівнює: |
|
|
Д. Дорівнює: |
-
Порівняти f´(x)
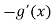 з нулем, якщо
з нулем, якщо 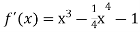 , а
, а 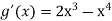
-
Розв’яжіть нерівність
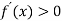 , якщо
, якщо 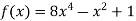 .
.
Тема №6. Застосування похідної
Урок №1

Застосування похідної
«…щоб стати математиком, треба захоплюватись
чарівністю закономірностей і логічною стрункістю законів»
У. Сойєр
Питання
- Ознаки сталості, зростання і спадання функції. Екстремуми функції
- Найбільше і найменше значення функції на відрізку.
- Побудова графіків функцій.
Література
Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту): Підручник для 10 класу закладів загальної середньої освіти. Київ: Генеза, 2018 рік, §§21 – 24, стор. 190 – 221.
|
1. Ознаки сталості, зростання і спадання функції. |
||
|
1.1 |
Ознака сталості функції. Функція |
|
|
1.2 |
Ознака зростання функції. Якщо |
|
|
1.3 |
Ознака спадання функції. Якщо |
|
|
1.4 |
Критичними точками функції називають внутрішні точки області визначення функції, у яких похідна дорівнює нулю, або не існує. |
|
|
1.5 |
Алгоритм дослідження функції
|
Знайти проміжки зростання і спадання функції |
|
1.6 |
Околом точки |
Околом точки 2 є проміжок |
|
1.7 |
Точку |
|
|
1.8 |
Точку
|
|
|
1.9 |
Точки максимуму і мінімуму називають точками екстремуму функції. |
|
|
1.10 |
Значення функції в точках екстремуму називають екстремумом функції( |
|
|
1.11 |
Якщо точка |
|
|
1.12 |
Ознака точок максимуму і мінімуму функції. Якщо при переході через точку |
|
|
1.13 |
Алгоритм дослідження функції на монотонність, екстремум: 1) знайти область визначення функції; 2) знайти похідну функції;
3) знайти критичні точки функції (розв’язати рівняння 4) позначити критичні точки на області визначення функції та знайти знак похідної на кожному з отриманих проміжків; 5) для кожної критичної точки за знаком похідної на проміжках зліва і справа від неї визначити, чи є вона точкою екстремуму, і якою саме, максимуму чи мінімуму. Записати результат. |
Знайти точки екстремуму функції |
|
2. Найбільше і найменше значення функції на відрізку |
||
|
2.14 |
Алгоритм пошуку найбільшого і найменшого значення функції на відрізку 1) знайти область визначення функції; 2) знайти критичні точки функції і серед них вибрати ті, які належать заданому проміжку; 3) обчислити значення функції у вибраних критичних точках і на кінцях заданого відрізка; 4) з усіх знайдених значень обрати найбільше і найменше. |
|
|
3. Побудова графіків функцій |
||
|
3.15 |
Алгоритм дослідження властивостей функції:
Дослідити функцію
|
|
Урок №2
«…бо мудрість увійде до серця твого,
і буде приємне знання для твоєї душі!»
Книга приповістей Соломонових 2:10
Фронтальне опрацювання матеріалу
Зростання і спадання функції. Екстремальні точки функції
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1. – 1.13 блоку № 6.
- Дайте відповіді на питання:
- Яку точку називають точкою максимуму функції?
- Яка ознака зростання функції?
- Яка ознака спадання функції?
- Яку точку називають точкою мінімуму функції?
- Що називають екстремумом функції і точками екстремуму?
- Які точки називають критичними?
- Сформулюйте ознаку точок максимуму і мінімуму.
- За яким алгоритмом досліджують функції на монотонність? Рис. 1
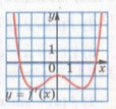
Завдання 2.
Усно виконайте вправи:
- На рисунку 1 зображено графік похідної функції.
Назвіть проміжки зростання функції. Рис. 2
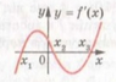
- На рисунку 2 зображено графік похідної функції.
Назвіть проміжки спадання функції.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконати письмово вправи:
-
Знайдіть проміжки монотонності функції
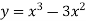 .
.
-
Знайдіть проміжки монотонності функцій: 1)
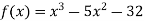 ; 2)
; 2) 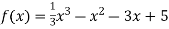 .
.
 Завдання 4.
Завдання 4.
Виконати письмово:
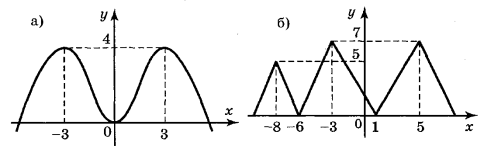
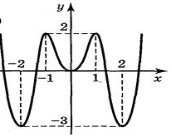
Для функцій, графіки яких зображено на рисунках а – г знайдіть точки максимуму і мінімуму функції:
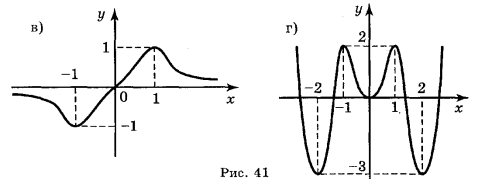
Завдання 5.
Виконати письмово:
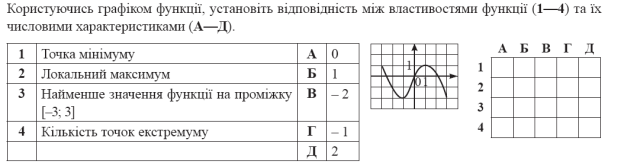
Завдання 6.
Письмово виконати вправи:
-
Знайдіть критичні точки функції
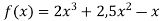 .
.
-
Знайдіть точки екстремуму функції та екстремум функції
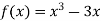 .
.
Урок №3
«…в порівнянні з Біблією всі людські
книги, навіть найкращі, є тільки планетами,
які запозичують своє світло і сяйво від Сонця»
Роберт Бойль англійський хімік, фізик і філософ
Фронтальне опрацювання матеріалу
Найбільше та найменше значення функції на відрізку
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 2.14 блоку № 6.
- Дайте відповіді на питання:
- Яка ознака точок максимуму і мінімуму функції?
- Які точки називають критичними?
- Які точки називають точками екстремуму функції?
- Сформулюйте ознаки зростання і спадання функції.
- Сформулюйте алгоритм дослідження функції на монотонність.
- Назвіть основні кроки алгоритму пошуку найбільшого і найменшого значення функції на проміжку.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Письмово виконати вправи:
- Знайти найбільше та найменше значення функції f(x) = x2 – 4x на проміжку [ -3; 3].
-
Знайдіть найбільше і найменше значення функції
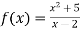 ,
,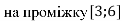 .
.
- Подайте число 60 у вигляді суми двох додатних чисел так, щоб сума їх квадратів була найменшою.
Завдання 3.
Письмово виконати вправи:
- Якими мають бути сторони прямокутника, периметр якого дорівнює 60 см, щоб його площа набувала найбільшого значення?
-
Знайти найменше значення функції
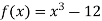 , на проміжку
, на проміжку 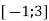 .
.
-
Знайти найбільше значення функції
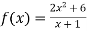 ,
,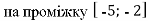
Уроки №4, 5
«…а ті, хто надію складає на Господа, силу
відновлять, крила підіймуть, немов ті орли, будуть
бігати і не потомляться, будуть ходити і не помучаться!»
Книга пророка Ісаї 40:31
Фронтальне опрацювання матеріалу
Дослідження функцій за допомогою похідної та побудова графіків функцій
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези блоку № 6.
- Усно дайте відповіді на питання:
- Сформулюйте ознаки сталості, зростання і спадання функції.
- Які точки називаються точками максимуму і мінімуму функції?
- Які точки називаються критичними точками функції?
- Яка ознака точок максимуму і мінімуму функції?
Завдання 2.
Чи вірне дане твердження:
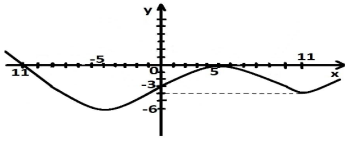
- Дана функція має дві критичні точки;
-
Функція має мінімум в точці
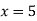 ;
;
-
Функція має максимум в точці
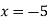
-
Функція зростає на проміжках:
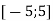 і [11; +
і [11; +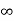 ];
];
-
Функція cпадає на проміжках: [
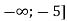 і [ 5; 11];
і [ 5; 11];
- Її графік симетричний відносно осі ОУ;
-
Нулі функції:
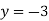 ;
;
- На проміжках (-∞; -5) і ( 5; 11) f '(х) < 0;
- На проміжках (-5; 5) і ( 11; ∞) f '(х) > 0.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
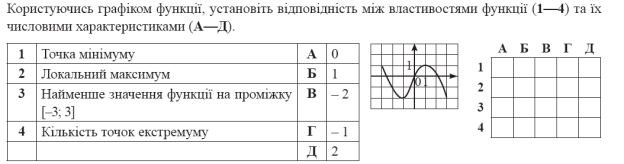
Завдання 3.
- Встановити відповідність між властивістю функції (1 – 3) та проміжками (А – Г), на яких виконується ця властивість.
|
1. |
Область визначення функції |
А |
|
|
2. |
Значення |
Б |
|
|
3. |
Значення |
В |
|
|
|
|
Г |
|
-
Побудуйте схематичний графік функції
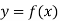 , визначеної на множині дійсних чисел, користуючись її властивостями, наведеними у таблиці.
, визначеної на множині дійсних чисел, користуючись її властивостями, наведеними у таблиці.
|
|
|
|
|
2 |
|
|
|
|
0 |
+ |
0 |
|
|
|
|
|
|
2 |
|
- Дослідити функцію за допомогою похідної та побудувати її графік:
-
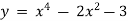 ;
;
-
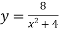 .
.
-
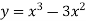
-
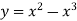
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Дослідіть функцію
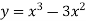 та побудуйте її графік.
та побудуйте її графік.
-
Дослідіть функцію
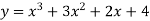 та побудуйте її графік.
та побудуйте її графік.
Урок №7
«Шукайте ж найперш
царства Божого й правди Його…»
Євангелія від Матвія 6:33
Внутрішньопредметне узагальнення матеріалу
Застосування похідної
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 6.
- Письмово відповісти на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2
Письмово виконайте вправи:
-
Кутовий коефіцієнт дотичної до графіка функції
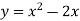 в точці
в точці 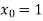 дорівнює:
дорівнює:
|
А |
Б |
В |
Г |
Д |
|
6 |
4 |
– 6 |
0 |
Інша відповідь |
-
Знайдіть проміжок спадання функції
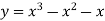 .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Функція
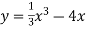 на відрізку
на відрізку 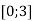 має найбільше та найменше значення, що відповідно дорівнюють:
має найбільше та найменше значення, що відповідно дорівнюють:
|
А |
Б |
В |
Г |
Д |
|
2 і – 2 |
0 і – 4 |
– 2 і – 3 |
4 і – 3 |
Інша відповідь |
Завдання 3.
Письмово виконайте вправи:
-
Функцію задано формулою
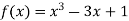 . Встановіть відповідність між завданнями (1 – 4) та відповідями (А – Д) на них.
. Встановіть відповідність між завданнями (1 – 4) та відповідями (А – Д) на них.
1 Розв’яжіть рівняння ![]() 3 Знайдіть проміжки спадання функції
3 Знайдіть проміжки спадання функції ![]()
2 Знайдіть координати точок 4 Знайдіть проміжки зростання функції ![]()
екстремуму функції ![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
За допомогою похідної дослідіть функцію
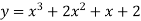 і побудуйте її графік.
і побудуйте її графік.
1


про публікацію авторської розробки
Додати розробку


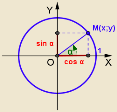


 за даними дослідження властивостей функції побудувати її графік.
за даними дослідження властивостей функції побудувати її графік.