Презентація "Центральні і вписані кути"
Про матеріал
Презентацію можна використати на уроках геометрії під час вивчення нового матеріалу та під час повторення даної теми. Презентація містить такі слайди:
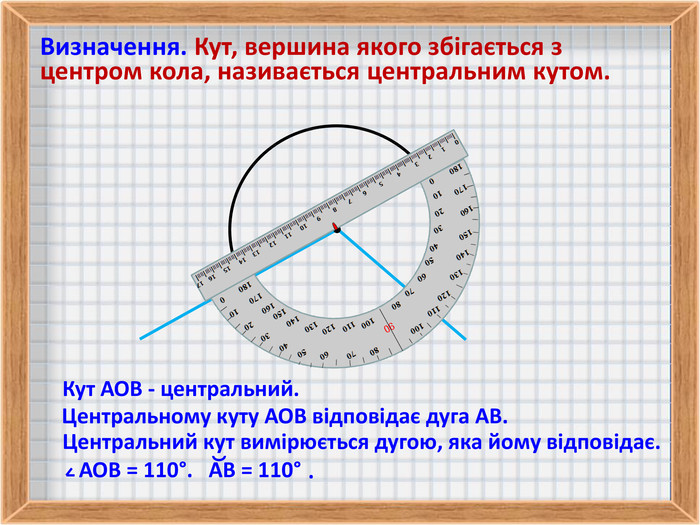
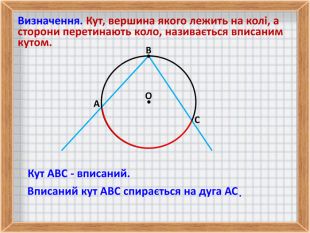
1. Визначення центрального кута.
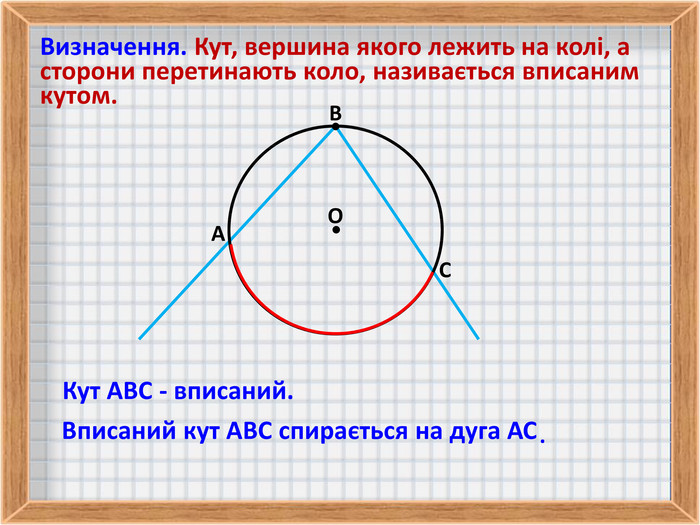
2. Визначення вписаного кута.
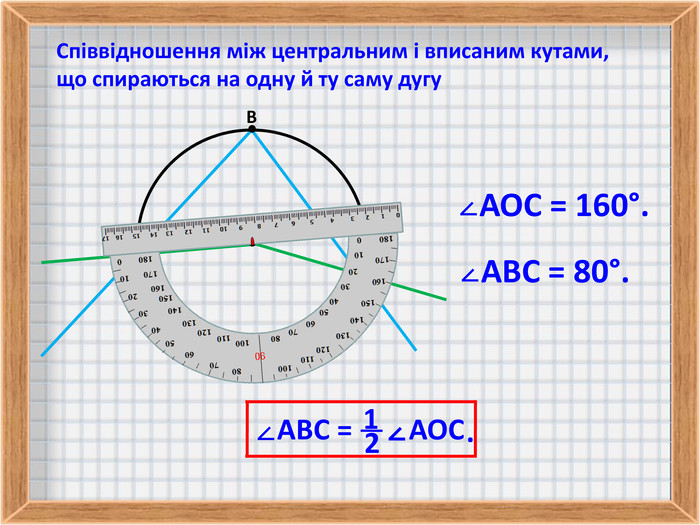
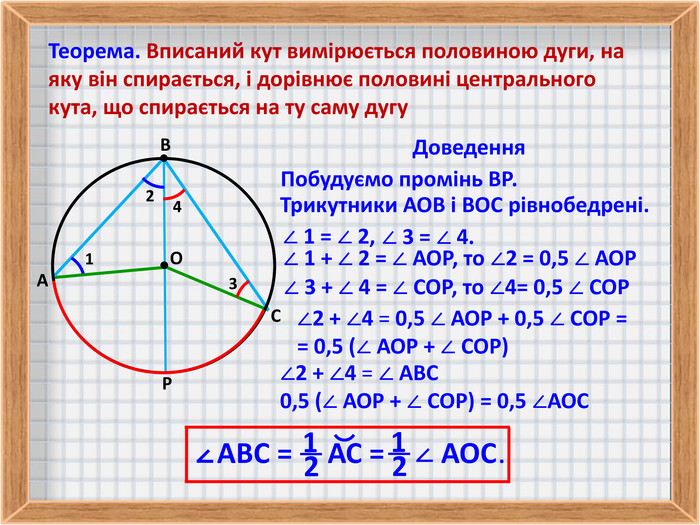
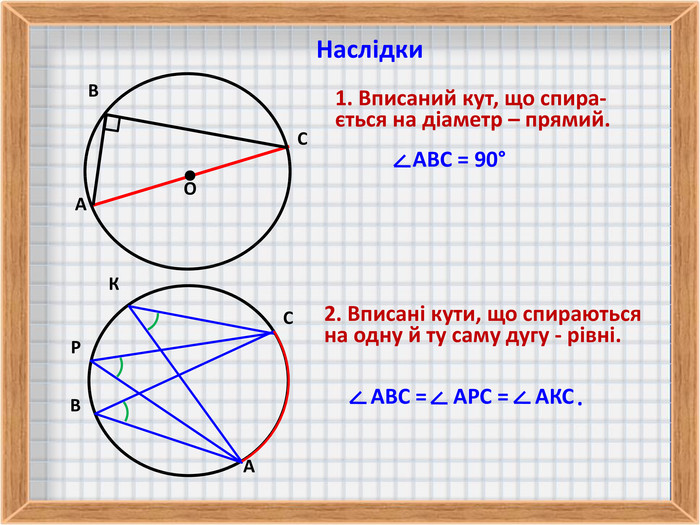
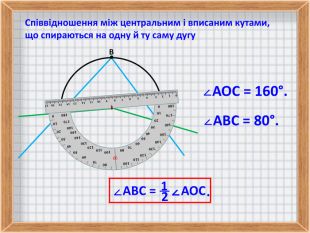
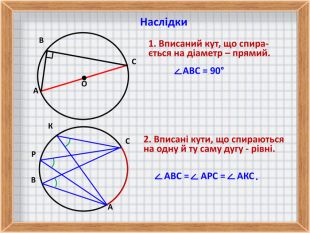
3. Співвідношення між центральним і вписаним кутами, що спираються на одну й ту саму дугу.
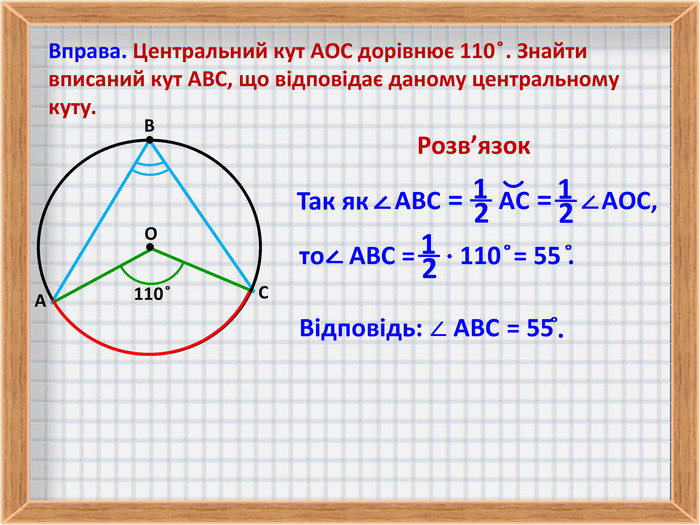
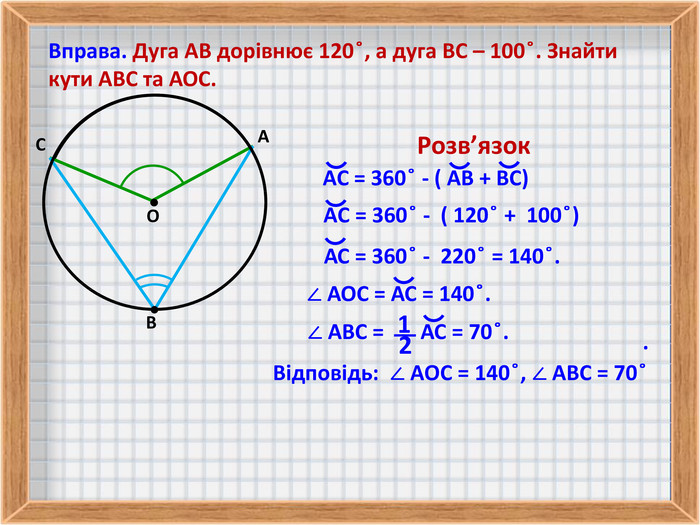
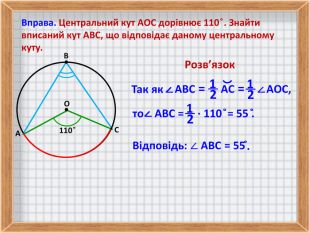
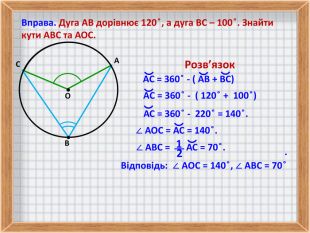
4. Розв'язування задач по даній темі.
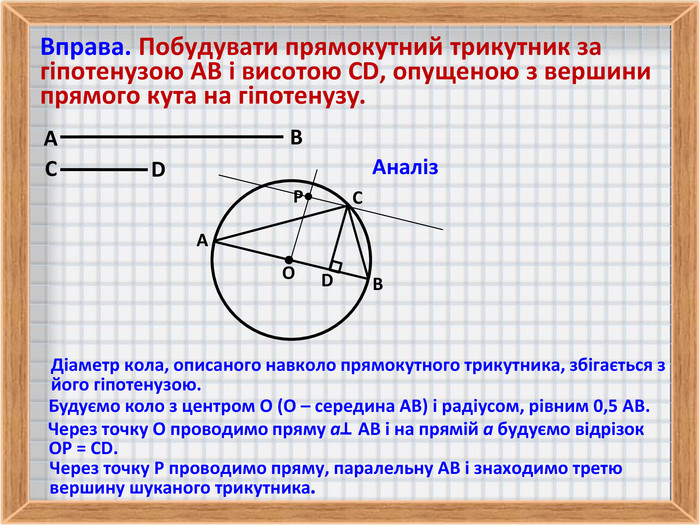
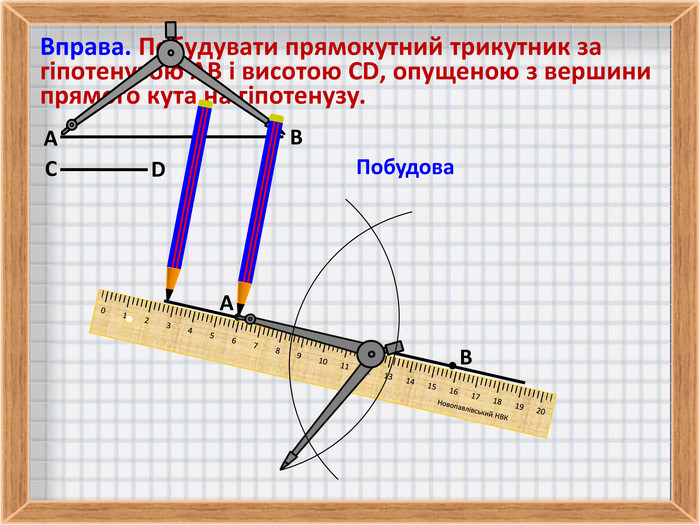
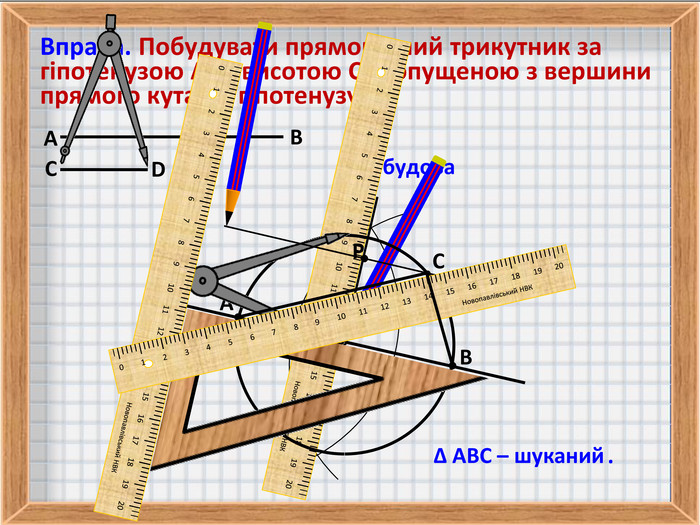
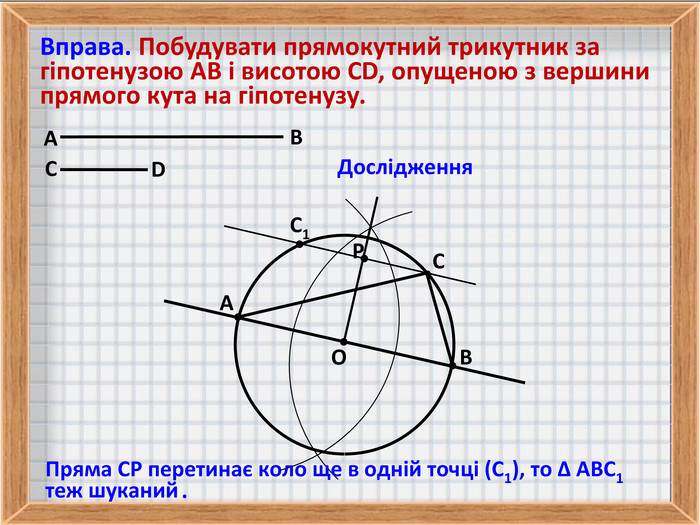
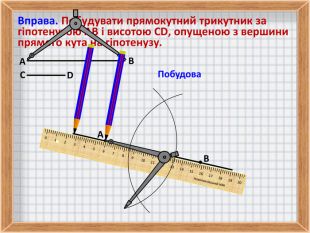
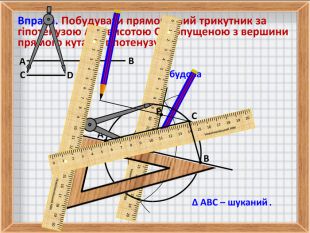
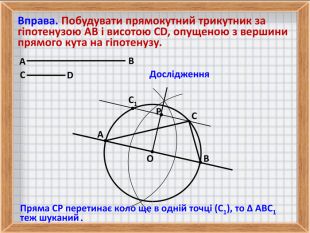
5. Вправа на побудову прямокутного трикутника за гіпотенузою і висотою, опущеною з вершини прямого кута на гіпотенузу.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку