Тема урока: «Теорема Пифагора»

Тема урока: «Теорема Пифагора»

 

Основная дидактическая цель урока - выучить теорему Пифагора, способствовать выработке и закреплению навыков применения теоремы Пифагора при решении задач.

 

Тип урока – урок изучения и применения новых знаний

 

Аспекты урока:

Образовательные

1. дать понятие о теореме Пифагора,
2. способствовать выработке и закреплению навыков применения теоремы Пифагора при решении задач,
3. расширить знания учащихся о жизни великого математика Пифагора,

Развивающие 

1. развитие слухоречевой и зрительной памяти учащихся,
2. развитие правильной устной и письменной математической речи,
3. развитие познавательного интереса к предмету геометрии.

Воспитывающие

1. продолжить воспитание у школьников аккуратности записей в тетради;
2. воспитание умений и навыков работы с учебником и дополнительной литературой по геометрии;
3. воспитание в детях уверенности в себе при ответах на уроке;
4. формировать позитивное отношение к ситуации взаимопроверки своих знаний.

 

Оборудование и материалы: мультимедийная установка, компьютерная презентация, учебники по геометрии

 

Методы:

• Словесный
• Иллюстративно-демонстрационный

 

На доске записано число, месяц, год данного урока, а также тема урока. Продолжительность урока – 45 минут.

№ п\п	Структура урока	Хронометраж урока, мин.
1	Организационный момент	2
2	Актуализация опорных знаний	10
3	Изучение нового материала	10
4	Закрепление новых знаний	18
5	Информация о домашнем задании	2
6	Оценивание	2
7	Подведение итогов по уроку	2

Суть истины вся в том, что нам она – навечно,

Когда хоть раз в прозрении её увидим свет,

И теорема Пифагора через столько лет

Для нас. Как для него, бесспорна, безупречна…

 

Ход урока

 

1. Организационный момент (2 мин)

Цель: подготовка учащихся к работе, активизация внимания для быстрого включения в деятельность.

Приветствие учащихся; проверка готовности к уроку.

 

2. Актуализация опорных знаний (10 минут)

• Какая фигура называется треугольником? (Треугольник – это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков соединяющих эти точки)
• Какие треугольники вы знаете? (Прямоугольный, равнобедренный, равносторонний)
• Какой треугольник называется равносторонний? (Равнобедренный треугольник – это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков соединяющих эти точки. Все стороны и углы этого треугольника равны)
• Какой треугольник называется равнобедренный? (Равнобедренный треугольник – это треугольник, в котором две стороны равны между собой по длинне)
• Какой треугольник называется прямоугольным? (Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть составляет 90 градусов)

 

 

 

 

 

3. Изучение нового материала (10 минут)

 

1. Немного истории

Теорема Пифагора  наверно самая известная теорема. Она имеет большую историю. Сегодня  урок начнем с истории этой великой теоремы.

 

Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т. е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий.

В вавилонских текстах она встречается за 1200 лет до Пифагора. В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила веревки», 600 год до н.э.), представляющем собой своеобразную инструкцию по сооружению алтарей в храмах, даются правила построения прямых углов при помощи веревки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины). Алтари по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта.

По-видимому, он первым нашёл её доказательство. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». В связи с этим более правдоподобной можно считать следующую запись: «… когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».

На протяжении последующих веков были найдены другие доказательства теоремы Пифагора. В настоящее время их насчитывается более пятисот.

 

2. Изучение нового материала

 

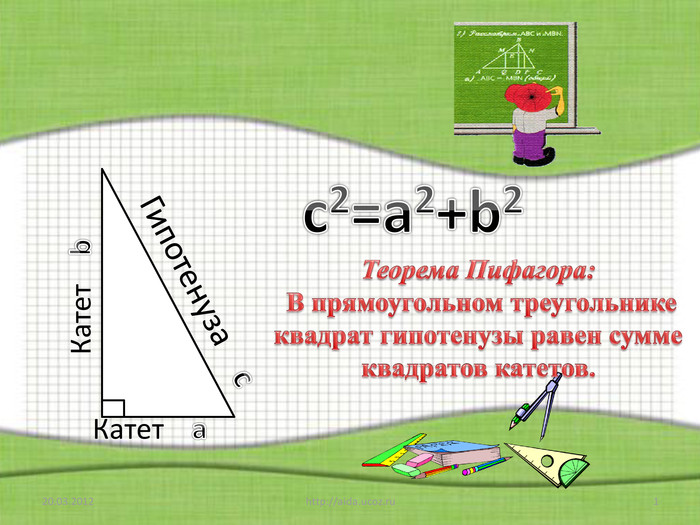
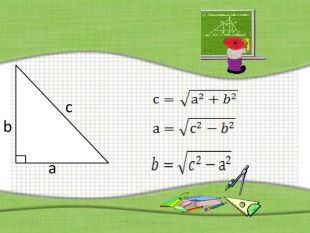
    c         c – гипотенуза

b а, b - катеты

 

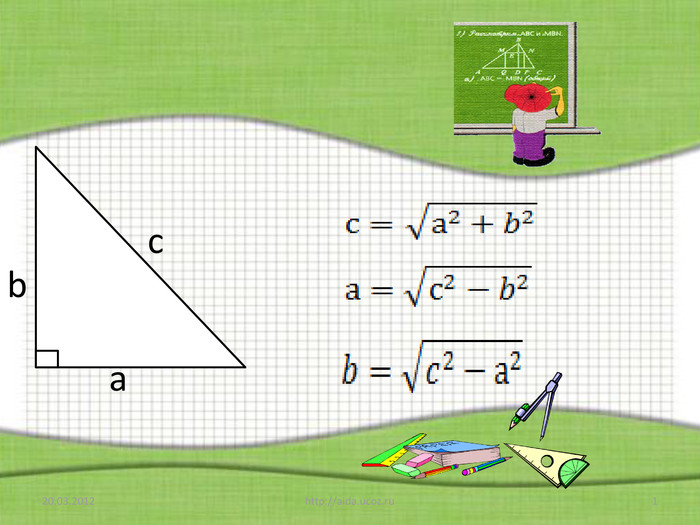
а

 

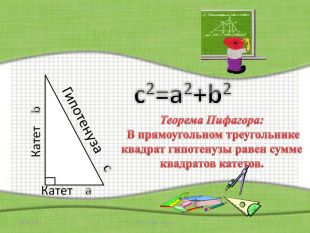
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

с  b                          а	с b    а	с b                        а

 

 

 

 

 

 

4. Закрепление новых знаний (18 минут)

 

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдём:

Катеты в квадрат возводим,

Сумму степеней находим –

И таким простым путём

К результату мы придём.

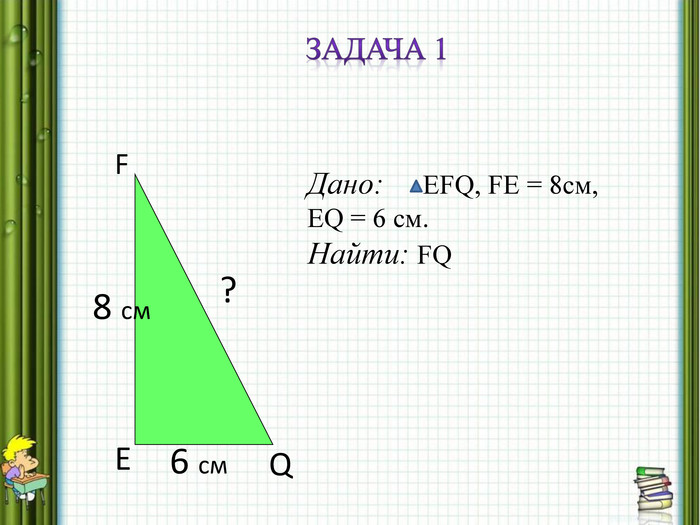
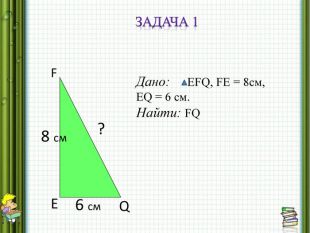
Задача 1.

В Прямоугольном треугольнике EFQ  катеты равны 8 см и 6 см. Найдите гипотенузу.

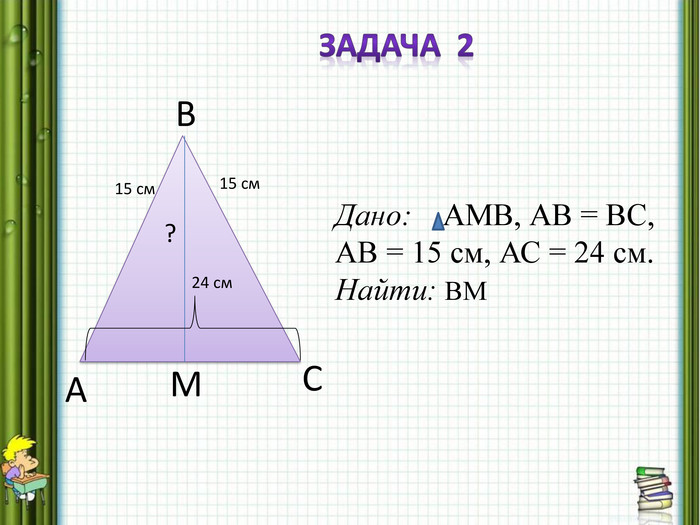
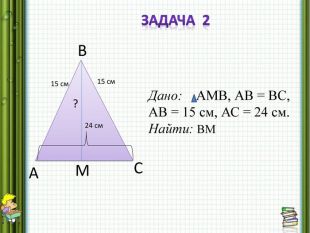
Задача 2.

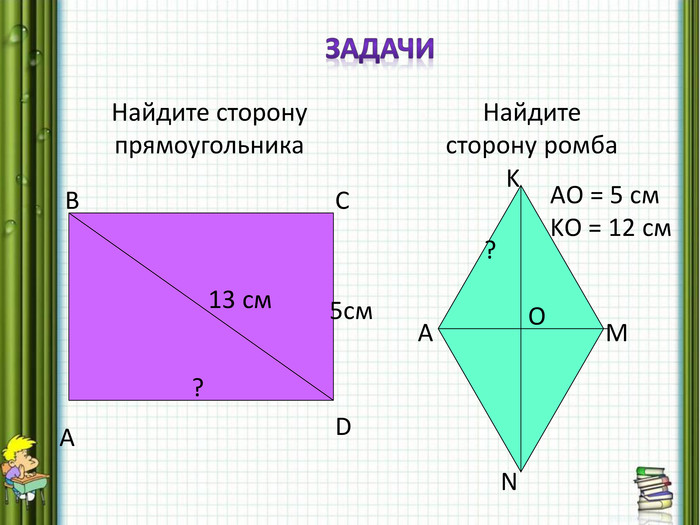
В треугольнике АВС  АВ равно ВС, ВС = 15 см.. Найдите  прямую делящую сторону АС пополам, если АС = 24 см.

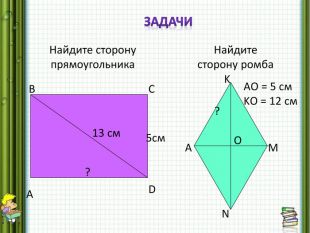
Задача 3

Решите задачи по рисункам, данным на слайде 15.

5. Информация о домашнем задании

Основное:  Прочитать  параграф 20,выучить формулы , стр.169 №  844 Дополнительное: стр. 173 № 886

6. Оценивание

Учитель оценивает учеников работающих на уроке, выставляет им оценки и объяснят их.

7. Подведение итогов по уроку

1. Что нового вы узнали на уроке?
2. Чему научились на уроке?
3. Что понравилось вам сегодня на уроке?
4. Что не понравилось вам на уроке?
5. Что непонятного было?