Презентація "Чотири чудові точки трикутника"
Про матеріал
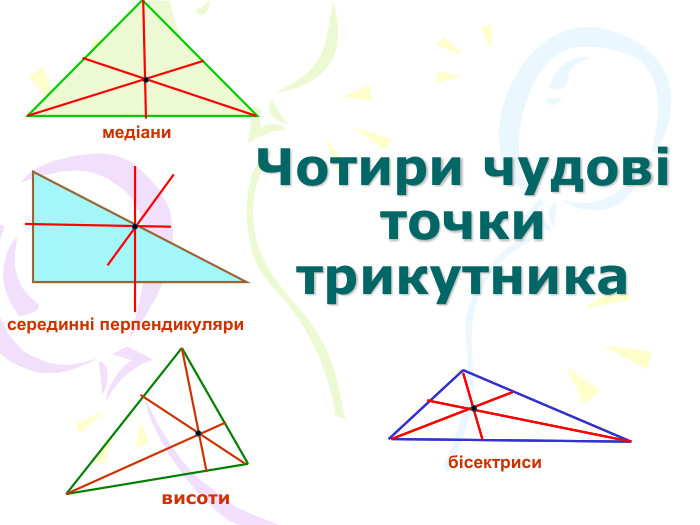
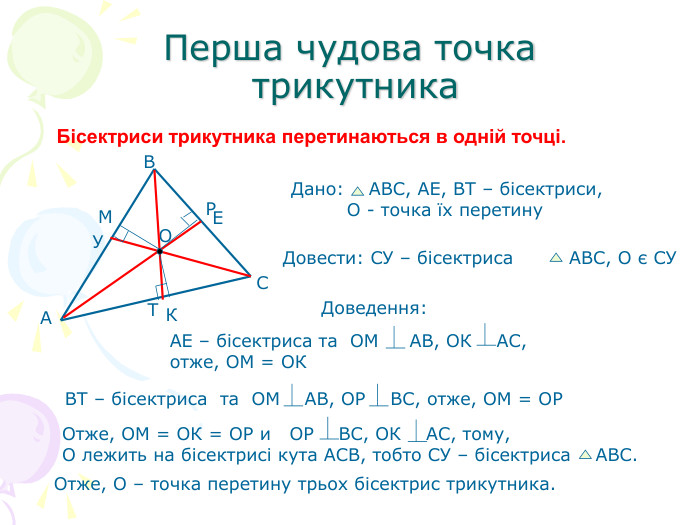
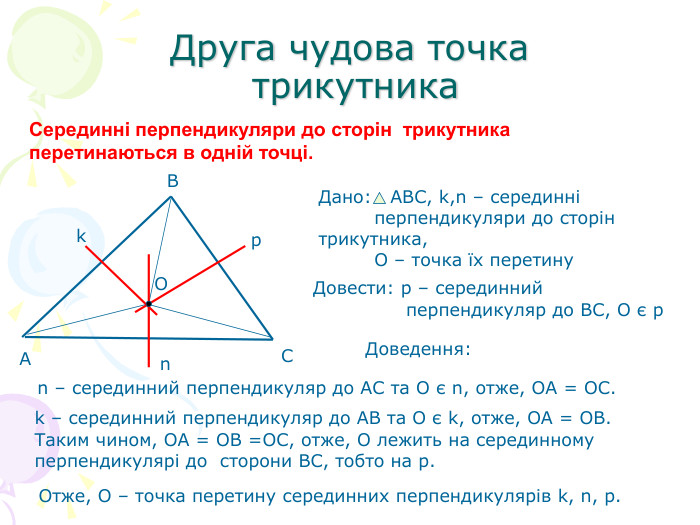
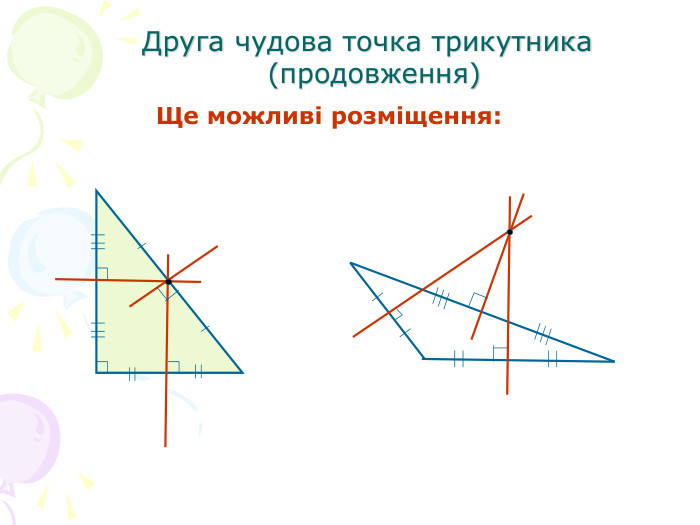
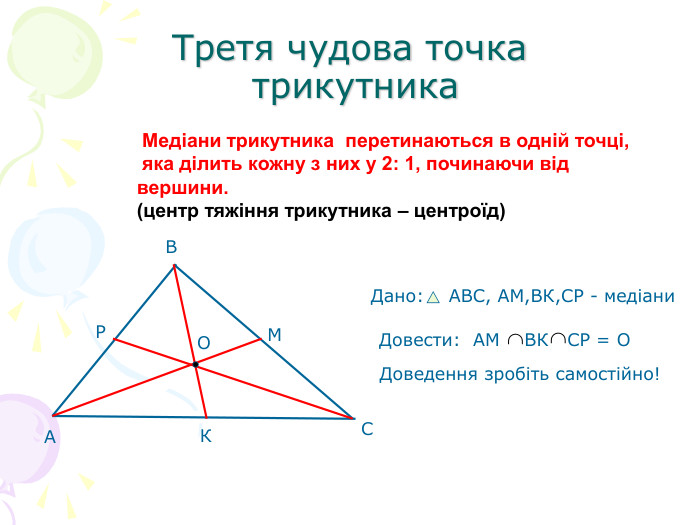
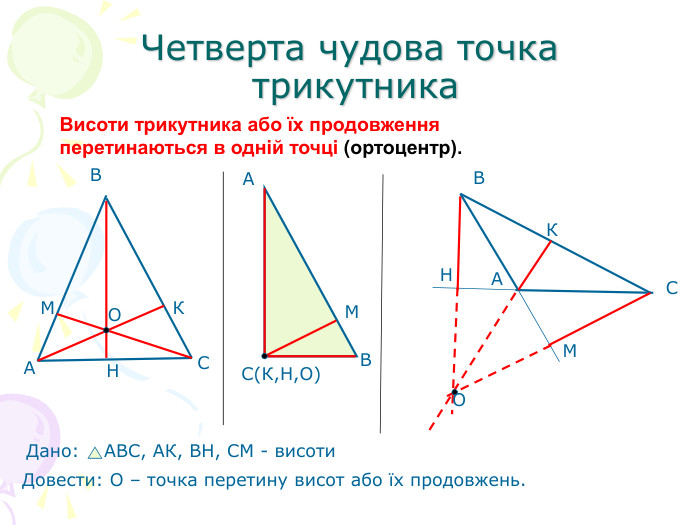
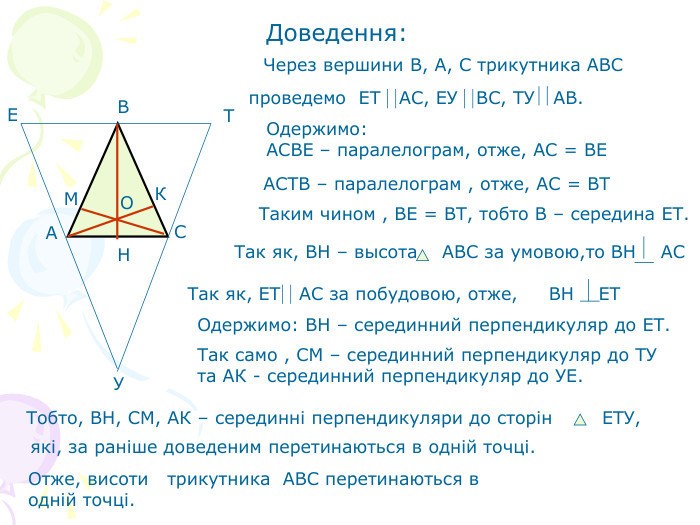
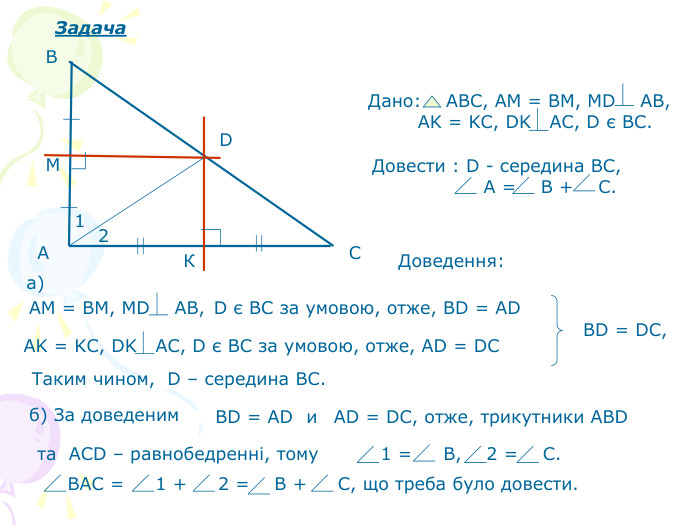
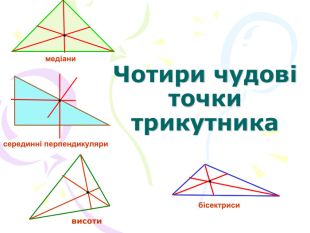
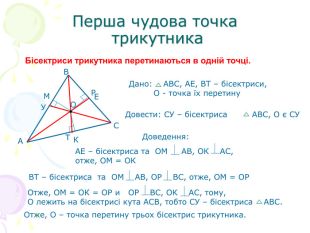
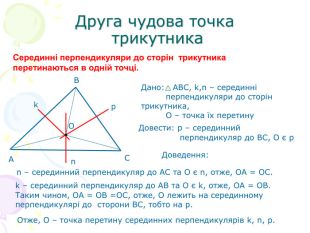
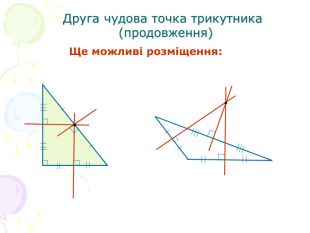
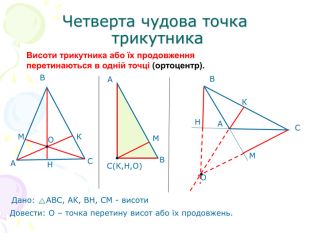
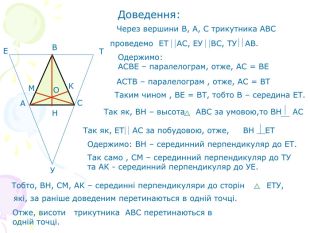
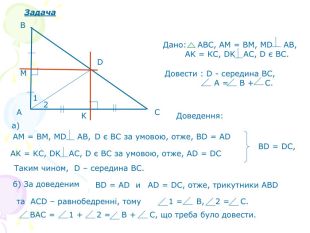
В презентації "Чотири чудові точки трикутника" розглянуті властивості бісектрис, медіан, висот трикутника, а саме, точки їх перетину. Матеріал можна використати як на позакласних заходах з математики, так і на уроках геометрії. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку