Презентація "Чотирикутник"
Про матеріал
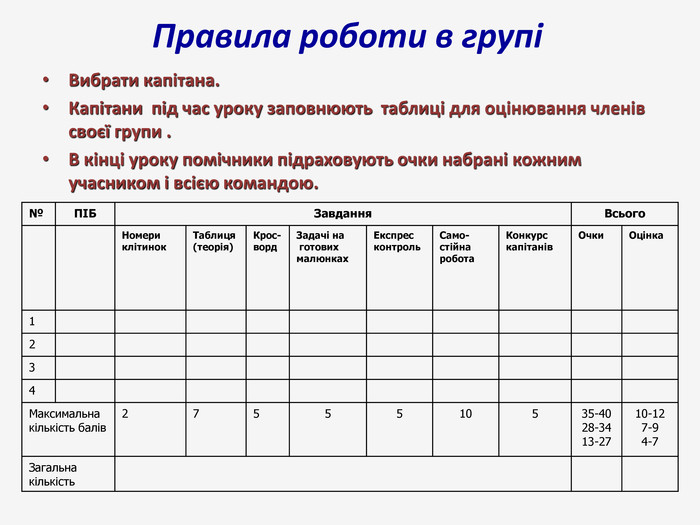
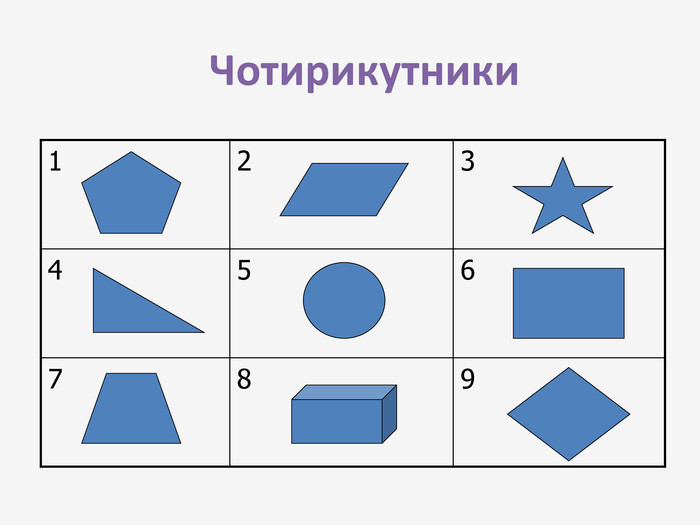
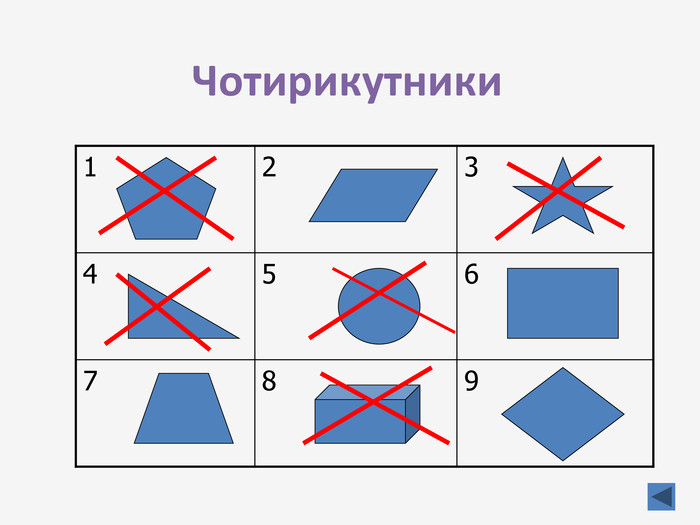
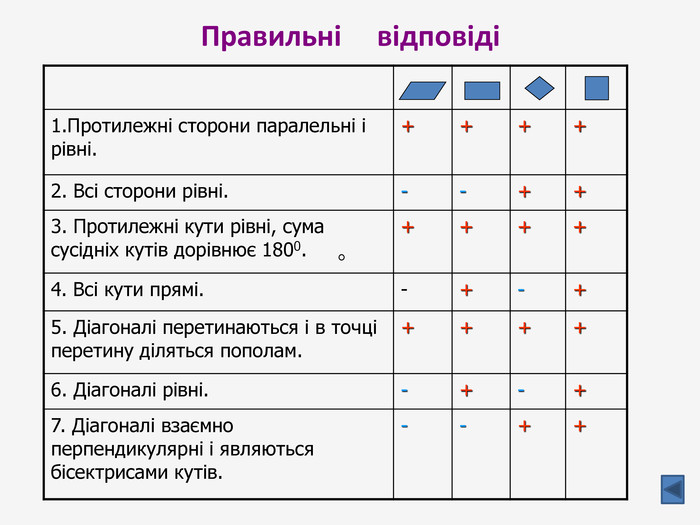
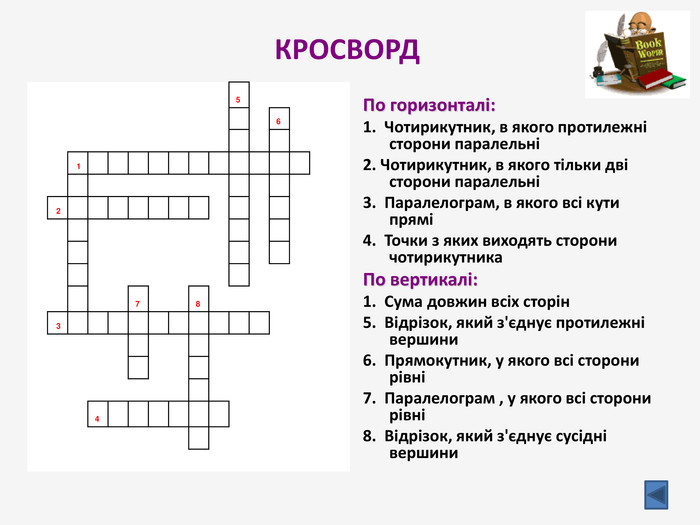
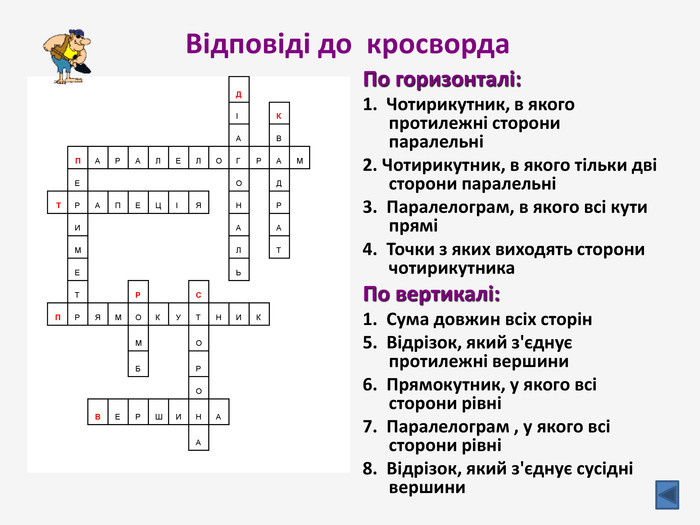
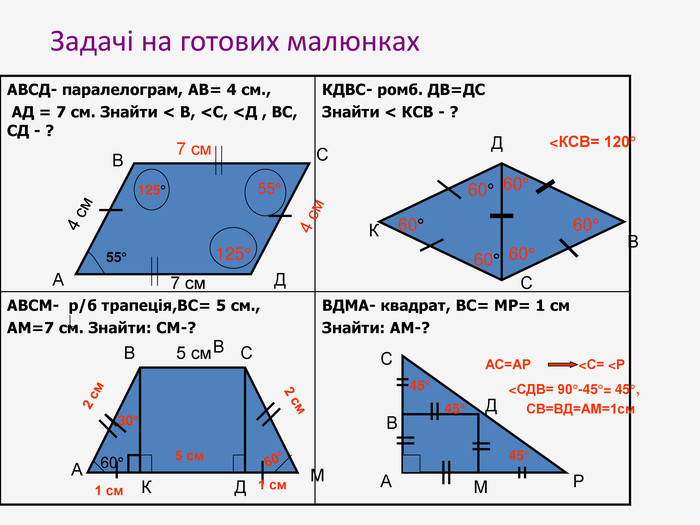
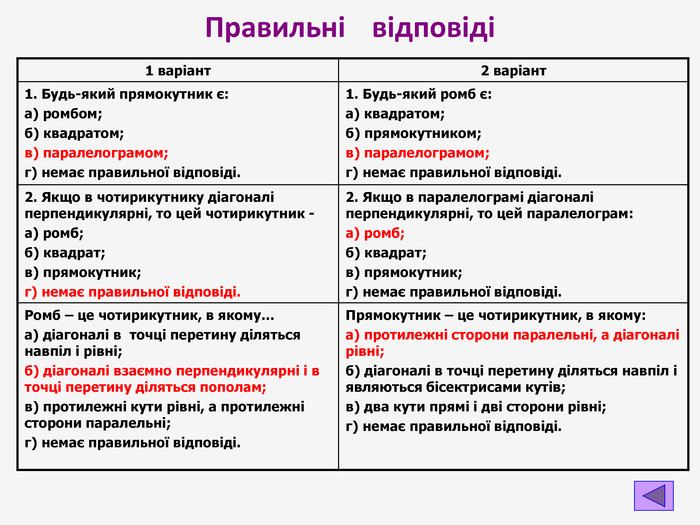
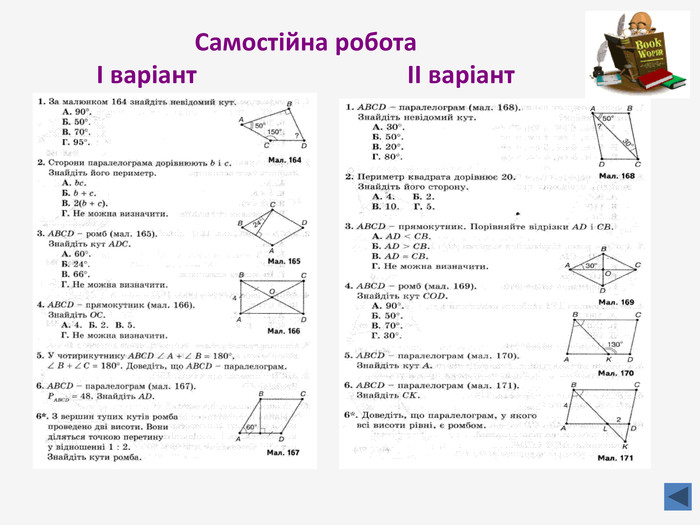
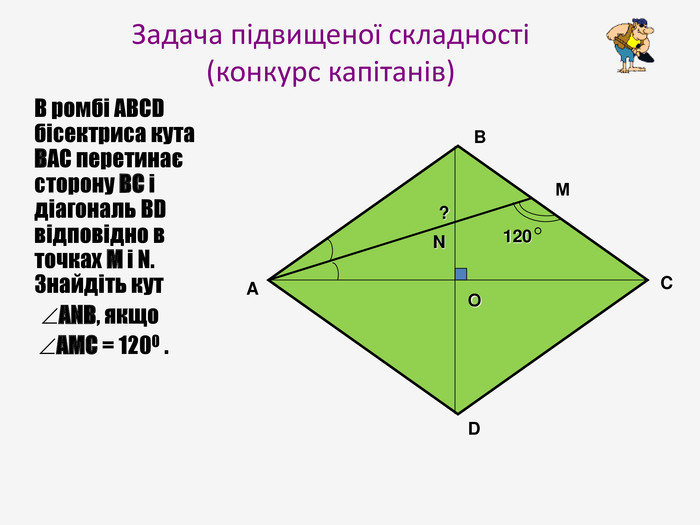
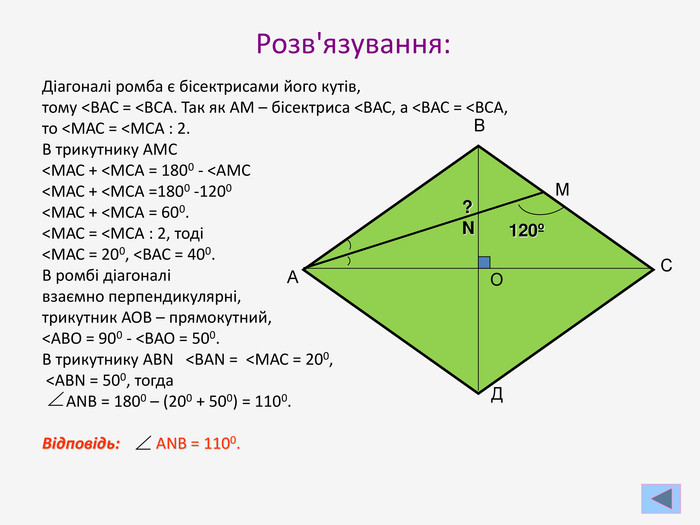
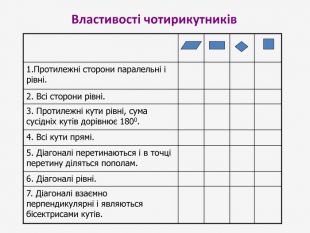
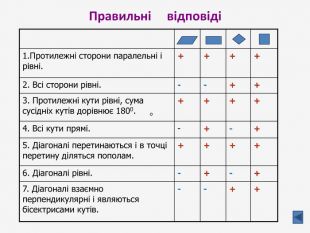
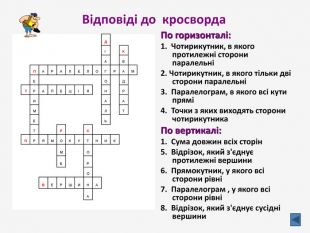
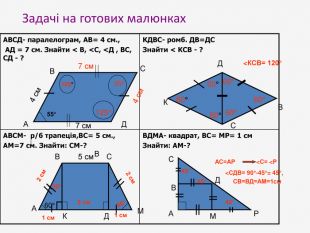
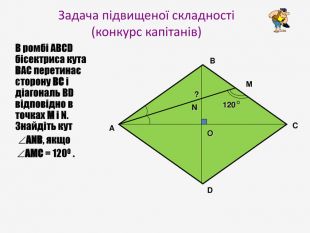
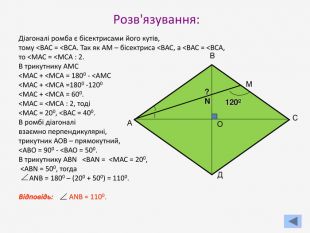
Презентація до узагальнюючого уроку з теми "Чотирикутник". Чотирикутник запрошує у подорож чудовою країною. Він поведе нас в цікавий захоплюючий світ. І для того, щоб ця подорож була цікавою, вам потрібно згадати все те, що ми вчили на минулих уроках, бути активними, старанними та уважними. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку