Презентація "Цікаві задачі в “Арифметиці Л.П. Магніцького " (2)

Цікаві задачі в “Арифметиці”Л. П. Магніцького (2)Л. П. Магніцький вчить в “Арифметиці” десятичному обчисленню. Що цікаво, він приводить таблицю додавання і множення не в тому вигляді, як її прийнято зараз видавати , а тільки її половину. Керівник гуртка «Розвиток математичних здыбностей»Т.І. Єрьоміна

“Арифметика сіреч наука числительная”У підручнику розглядається і геометрія. Наприклад, теорема Піфагора вивчається на завданні про вежі деякої висоти і сходах певної довжини. Наскільки потрібно відсунути нижній кінець драбини, щоб її верх збігся з верхом вежі? Вивчається і геометрія кола, вписаних багатокутників. Всі завдання, які використовуються в книзі, життєві.

Арифметичні ігри Л. П. Магніцького Як дізнатися день тижня?          Перенумерувати дні тижня, починаючи з понеділка, по порядку з 1 до 7, запропонуйте загадати день тижня. Запропонуйте порядковий номер задуманого дня збільшити в 2 рази і до цього добутку додати 5. Отриману суму запропонуйте помножити на 5, а потім те, що вийде, помножити на 10. За оголошеним результатом ви називаєте день тижня, який був загаданий.

Арифметичні ігри Л. П. Магніцького. Відгадати кілька чисел. Запропонуйте задумати кілька (вам відома кіл-ть) однозначних чисел. Перше з задуманих чисел помножити на 2 і додати 5. Число помножити на 5 і до того, що вийде, додати 10 і друге задумане число. Потім треба стільки раз, скільки залишилося невикористаних задуманих чисел, проводити такі операції. Множити отримане від попередніх дій число, але 10 і до добутку додати чергове задумане число. Після оголошення результату запропонованих вами дій, ви оголошуєте, які числа були задумані.

Арифметичні ігри Л. П. Магніцького У кого кільце? Перенумерувати присутніх і відвернувшись від них, пропонуєте кому-небудь взяти кільце і одягнути його на якусь руку на палець. Потім попросіть подвоїти порядковий номер того, хто взяв кільце, і до отриманого результату додати 5. Отриману суму попросіть помножити на 5 і до неї додати номер пальця, вважаючи з мізинця. Отриману суму попросіть знову помножити на 10, до результату додати число 1, якщо кільце одягнуте на ліву руку і число 2, якщо кільце одягнуте на праву руку. Після оголошення результату запропонованих арифметичних дій ви відгадаєте, хто з присутніх, взяв кільце і на який палець, який руки надів його.  

Цікаві властивості чисел. Множення на пальцях. Ось як його описує Магніцький на прикладі множення 7 на 7. Загнемо на лівій руці стільки пальців, на скільки перший співмножник перевищує 5, а на правій руці стільки пальців, на скільки другий співмножник перевищує 5. У розглянутому прикладі на кожній з рук буде загнуто по 2 пальця. Якщо скласти кількість загнутих пальців і перемножити кількість незагнутих, то вийдуть відповідно числа десятків і одиниць шуканого числа (в даному прикладі 4 десятка і 9 одиниць). Якщо цим способом обчислювати 6 * 7, то отримаємо 3 десятка і 12 одиниць, тобто 30 + 12 = 42. Так можна обчислювати твори будь-яких однозначних чисел, більших ніж 5.

Цікаві властивості чисел. Множення на 9. 1й спосіб. Покласти обидві руки поруч на стіл і витягнути пальці. Нехай кожен палець по порядку зліва направо означає число від одного до десяти. Для того щоб помножити будь-яке число на 9, досить, не зрушуючи рук зі столу, підняти вгору той палець, який позначає перший множик. Тоді пальці, що лежать зліва від піднятого, покажуть число десятків добутку, а пальці справа - число одиниць. Наприклад: 6 помножити на 9. Вгору піднят шостий (великий) палець правої руки. Число десятків добутку дорівнює 5, стільки пальців лежать зліва. А число одиниць дорівнює 4, стільки пальців лежать справа.

Цікаві властивості чисел. Множення на 9. 2спосіб. Якщо розглянути таблицю помноження на 9, то очевидно, що число десятків в добутку завжди на одиницю менше, ніж те число, на яке множимо 9, а сума цифр одиниць і десятків у добутку завжди дорівнює 9. Знаючи це, легко порахувати , що 3 * 9 буде 27, бо число десятків на один менше ніж 3, тобто 2; 9 - це 2 і 7, число одиниць в добутку дорівнює 7.

Цікаві властивості чисел. Однакові цифри. Якщо помножити число 777 на число 143, то вийде шестизначне число, що записується одними одиницями: 111 111. Якщо ж число 777 помножить на 429, то получимо число 333 333, що записується шістьма трійками. Знайдіть, на які числа треба помножити число 777, щоб отримати шестизначні числа, записані одними двійками, четвірками, одними п'ятірками і т.д.

Старовинний спосіб вирішення завдань на змішання речовин. Як змішати масла? Розглянемо метод Л. П. Магніцького, який ми умовно назвали «рибкою» на прикладі задачі змішання масел. Задача 1. У чоловіка одного були масла на продаж. Одне - ціною десять гривень за відро, а інше - шість гривень за відро. Захотілося йому зробити з цих двох масел, змішавши їх, масло ціною сім гривень за відро. Питання: в яких пропорціях потрібно змішати ці два масла?

Старовинний спосіб вирішення завдання. У центрі пишемо ціну першого масла - 6. Під ним, відступивши вниз, пишемо ціну другого масла - 10. Зліва, приблизно посередині між верхньою і нижньою цифрами пишемо вартість бажаного масла. З'єднуємо три цифри відрізками прямих. Першу ціну, оскільки вона менша за ціну бажаного масла, віднімемо з ціни змішаного масла, і результат поставимо праворуч від другої ціни по діагоналі щодо першої ціни. Потім з другої ціни, яка більша за ціну бажаного масла, віднімемо ціну змішаного масла, а то що залишиться, напишемо праворуч від першої ціни по діагоналі до другої ціни. З'єднаємо точки відрізками, і отримаємо ось таку картину.

Потім визначаємо співвідношення отриманих справа величин між собою. Ми бачимо, що поряд з ціною дешевого масла є цифра 3, а поруч з ціною дорогого масла - цифра 1. Це означає, що дешевого масла потрібно взяти втричі більше, ніж дорогого, тобто для отримання масла ціною 7 гривень, потрібно взяти масла в пропорції 1 до 3, тоді дешевого масла повинно бути втричі більше, ніж дорогого масла. Сучасний спосіб вирішення завдання. Візьмемо одну частину дешевого масла за «X». А частина дорогого масла - за «Y» і отримаємо ось таке рівняння: 7 (x + y) = 6x + 10y 7x + 7y = 6x + 10y 7x-6x = 10y-7y x = 3y 1/3 = x / y Ми отримали, що масла потрібно змішати в пропорції 1 до 3

Старовинний спосіб вирішення завдань на змішання речовин. Чи може дана методика Магніцького в нагоді в сучасному житті? Звичайно, може, ось, наприклад, в перукарні. Задача 2. У нас є два розчину перекису водню: 30% і 3%. Потрібно отримати 12% розчин. Чи не допоможете нам правильно підрахувати пропорції? Сучасний спосіб вирішення завдання. Позначимо шукану частину 30% розчину - х, а 3% - розчину - y. Відповідно, треба отримати 0,12 (х + у). Запишемо рівняння: 0,03у + 0,3х = 0,12 (x + y) 0,3х-0,12х = 0,12у-0,03у 0,18х = 0,09у х = 2у Відповідь: для отримання 12% -го розчину потрібно взяти одну частину 30% розчину і дві частини 3% -го розчину перекису.

Старовинний спосіб вирішення завдання. У центрі пишемо концентрацію першого розчину - 30%. Під ним пишемо концентрацію другого розчину - 3% або 0, 03. Зліва, посередині між верхньою і нижньою цифрами пишемо концентрацію бажаного розчину - 12% або 0, 2. З'єднуємо три цифри відрізками прямих. З першої концентрації, оскільки вона більше бажаної, віднімемо 0,12, підпишемо праворуч від 0,03 результат 0, 18, який виявився по діагоналі від 0,3. З 0, 12 віднімаємо 0, 03 і підписуємо праворуч від 0,3 результат - 0,09, який теж виявляється по діагоналі від значення 0, 03. З'єднуємо всі відрізками і отримуємо «рибку» . Співвідношення отриманих величин - 0, 09 і 0,018 - становить 1 до 2, т. Е. Першого розчину концентрацією 30% треба взяти в 2 рази менше, ніж 3% -го розчину.

Задача 3. Сплави. Є два сплави з різним вмістом золота. У першому сплаві - 35% золота, а в другому 60%. В якому відношенні треба взяти перший і другий сплав, щоб отримати з них новий, сплав, який містить 40% золота. Старовинний спосіб вирішення завдань на змішання речовин. Сучасний спосіб вирішення завдання. Нехай частина першого сплаву - х, а другого – у. Тоді кількість золота в першому сплаві становить 0, 35х, а в другому - 0,6у. Маса нового сплаву дорівнює х + у, а кількість золота становить 0,4 (х + у). Складемо рівняння: 0, 35х + 0,6у = 0,4 (х + у); 35х + 60у = 40х + 40у; 20у = 5х х / у = 4/1 Відповідь: для отримання сплаву, що містить 40% золота з двох сплавів з вмістом 35% і 60%, потрібно взяти в 4 рази більше 35% -го сплаву.

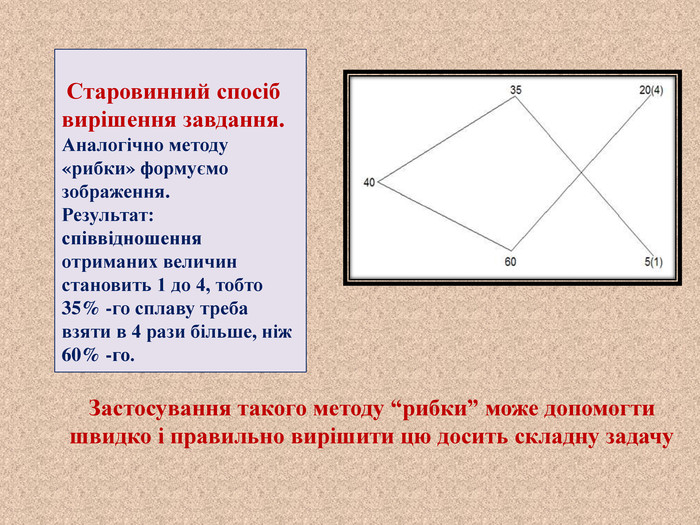
Старовинний спосіб вирішення завдання. Аналогічно методу «рибки» формуємо зображення. Результат: співвідношення отриманих величин становить 1 до 4, тобто 35% -го сплаву треба взяти в 4 рази більше, ніж 60% -го. Застосування такого методу “рибки” може допомогти швидко і правильно вирішити цю досить складну задачу

Задачи на потрійне правило. ПОТРИЙНЕ ПРАВИЛО: перемножити друге і третє число і добуток розділити на перше Задача 1. Сталева кулька об'ємом 6 кубічних сантиметрів має масу 46,8 г. Яка маса кульки з тієї ж стали, якщо її об'єм2,5 кубічних сантиметра? (Пряма пропорційність). Рішення. 6 - 46,8 - 2,5 (рядок)46,8 × 2,5 : 6 = 19,5 (г) х = 19,5 (г) Відповідь: 19, 5 г .

Задачі на потрійне правило. Задача 2. З 21 кг бавовняного насіння отримали 5,1 кг масла. Скільки масла вийде з 7 кг бавовняного насіння? (Пряма пропорційність). Рішення. 21 - 5,1 - 7 (рядок) 5,1 × 7: 21 = 1,7 (кг) х = 1,7 (кг) Відповідь: 1,7 кг.

Задачі на потрійне правило. Задача 3. Для будівництва стадіону 5 бульдозерів розчистили майданчик за 210 хв. За якийсь час 7 бульдозерів розчистили б цей майданчик? (Зворотна пропорційність) . Рішення.7 - 5 - 210 (рядок) 210 × 5: 7 = 150(хв.) х = 150 (хв.) Відповідь: 150 хв.

Задачі на потрійне правило. Задача 3. Для перевезення вантажу знадобилося 24 машини вантажопідйомністю 7,5 т. Скільки потрібно машин вантажопідйомністю 4,5 т, щоб перевезти той же вантаж? (Зворотна пропорційність). Рішення. 4,5 - 24 - 7,5 (рядок) 24 × 7,5: 4,5 = 40 (машин) х = 40 (машин) Відповідь: 40 машин.

ДО НОВИХ ЗУСТРІЧЕЙ