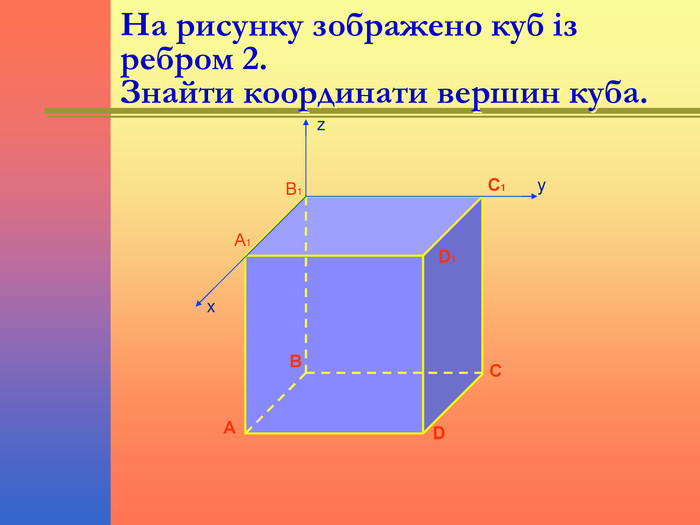
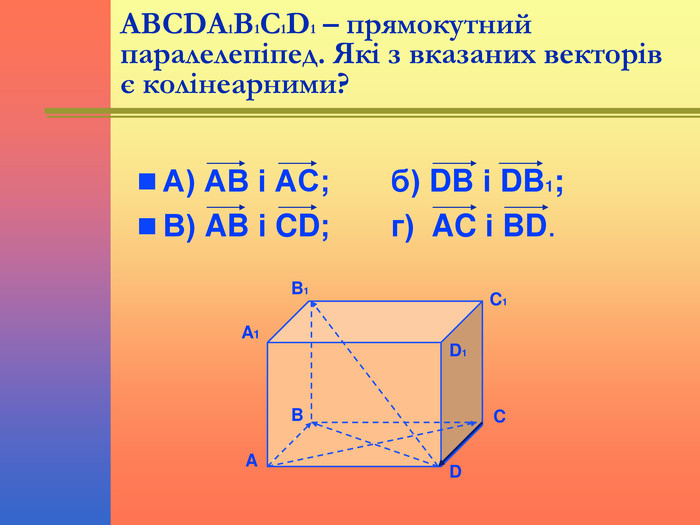
Презентація "Декартові координати і вектори в просторі. Тести"
Про матеріал
Матеріал допоможе вчителю математики ефективно перевірити рівень знань з даної теми раціонально використавши час на уроці. Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку