Презентація "Десяткові дроби. Порівняння десяткових дробів"
Про матеріал
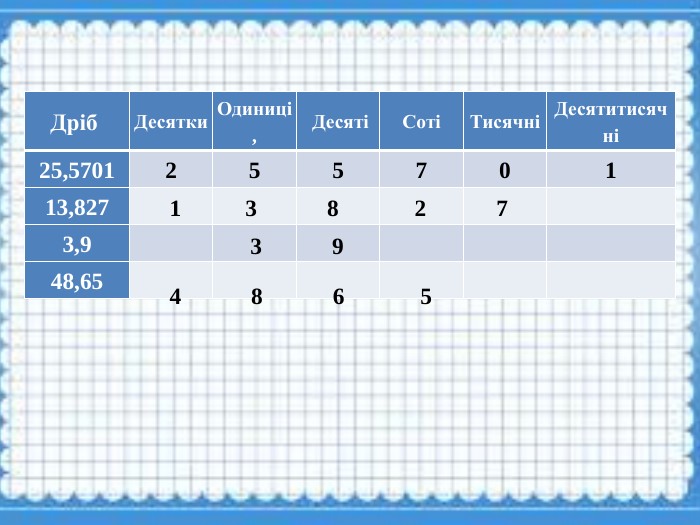
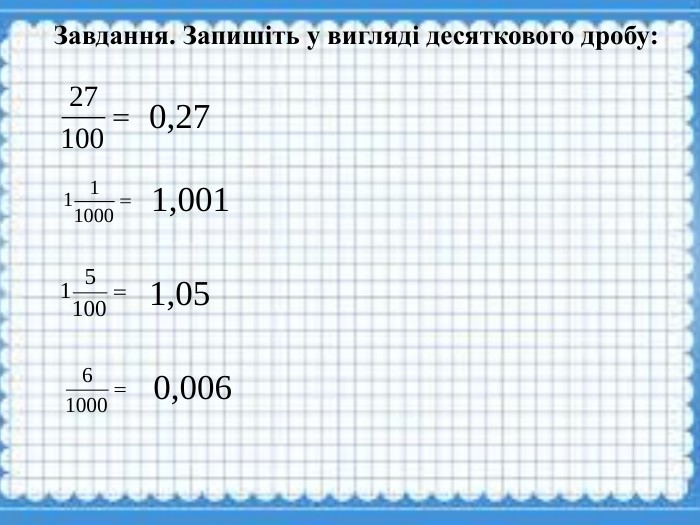
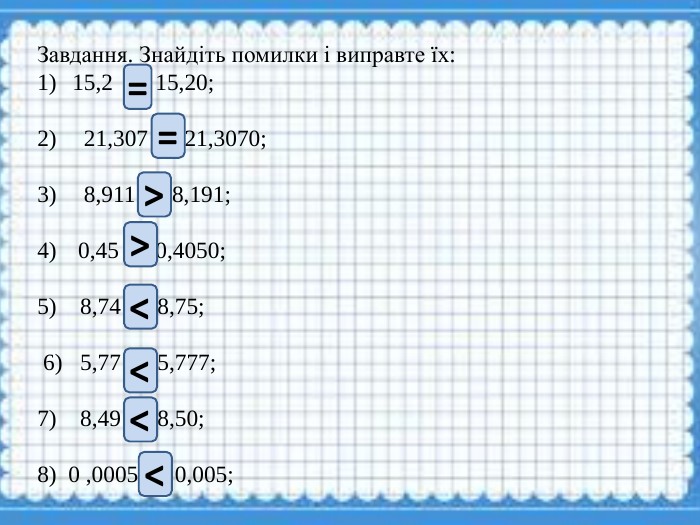
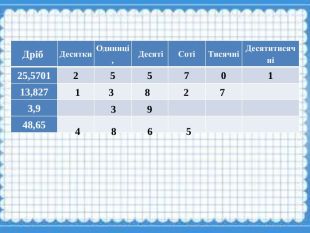
Презентація для проведення уроків узагалюнюючого повторення з теми "Десяткові дроби. Порівняння десяткових дробів" Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку