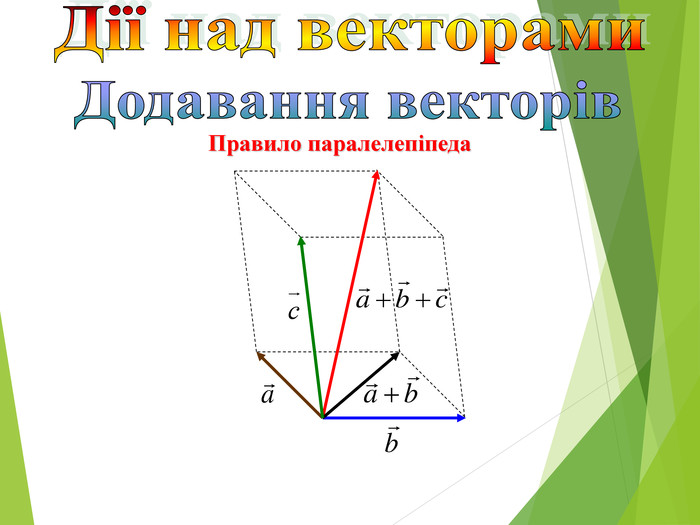
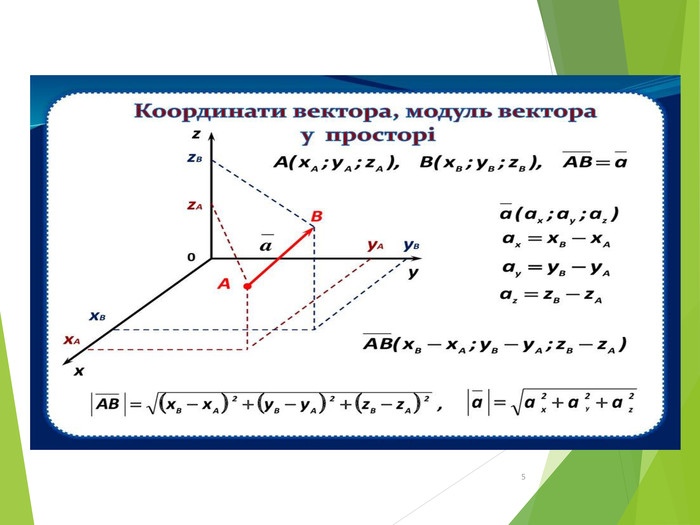
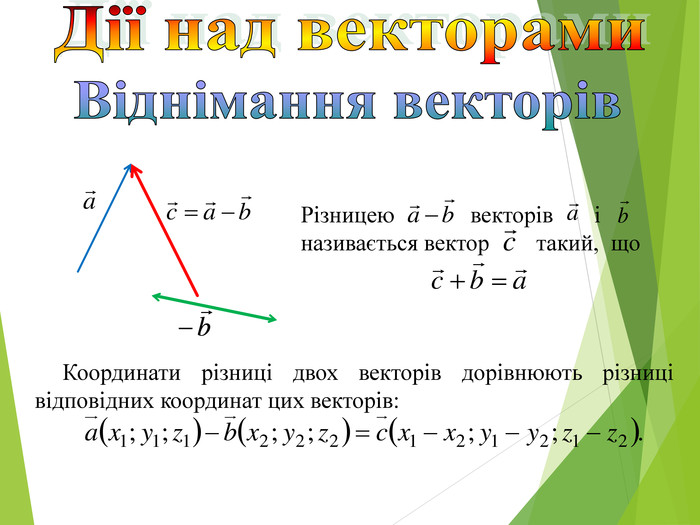
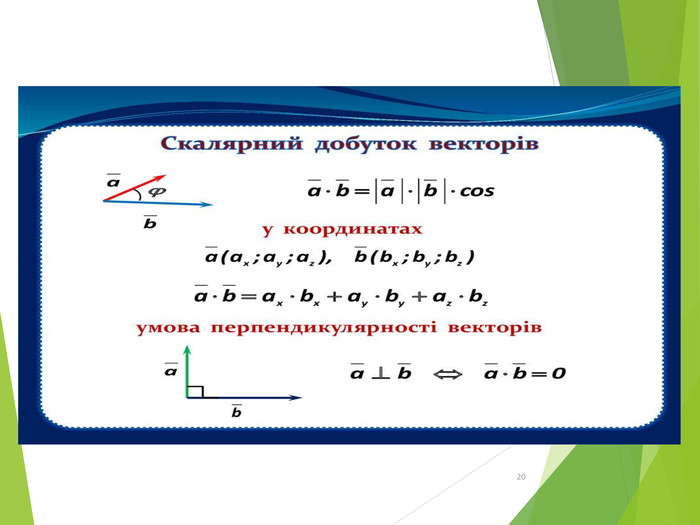
Презентація "Дії_над_векторами"
Про матеріал
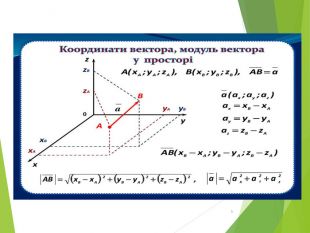
Презентація допоможе повторити та узагальнити знання з теми “Вектори у просторі»;. застосовувати властивості векторів та формули при розв’язуванні задач прикладного змісту. Розвивати просторову уяву , математичну та ключові компетентності. Виховувати почуття відповідальності за отриманні знання, мотив позитивного відношення до навчання. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Змістовно. Дякую!
-
ppt
До підручника
Геометрія (академічний рівень) 10 клас (Біляніна О.Я., Біляніна Г.І., Швець В.О.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку