Презентація до дослідницької роботи "Застосування різних методів для обчислення площі Карачунівського гранітного кар'єру"

Застосування різних методів для обчислення площі карачунівського гранітного кар'єру

Мета роботи – оволодіння різними способамиобчислення площ фігур, обґрунтування раціональності використання даних методів та порівняння отриманих результатів. Об'єктом дослідження є методи вимірювання площі фігур довільної форми : метод зважування, застосування палетки, застосування калькулятора виміру площі, застосування формул, розбиття многокутника на прямокутні трикутники, прямокутники, квадрати, метод добудови до прямокутника, формула Піка, знаходження площі за координатами вершин. Предметом дослідження є застосування опрацьованих методів для вимірювання площі Карачунівського гранітного кар’єру, що має довільну форму . Гіпотеза: площа складної фігури може бути виміряна наближеними методами з достатньою точністю для практичних цілей.

Завдання дослідження:- Вивчити за літературними джерелами історію виникнення та використання площі фігури від минулого до сьогодення. - Ознайомитися з різними формулами обчислення площ фігур та одиницями їх вимірювання.- Дослідити різні способи знаходження площі опуклих та не опуклих многокутників.- Визначити площу Карачунівського гранітного кар’єру різними методами.- Проаналізувати отримані результати, зробити висновок про практичне застосування знаходження площі фігури неправильної форми. Методи дослідження- Вивчення та аналіз теоретичних відомостей з даного питання: робота з навчальної та науково-популярною літературою, пошук інформації в Інтернеті. - Порівняння, зіставлення, аналіз, аналогія.-Графічне моделювання, аналіз і класифікація отриманих результатів.

Над знаходженням площі працювали багато вчених: АрхімедЄгиптяни та греки Герон. Бонавентура КавальєріЙоганн Кеплер. Георг Пік

Площа — фізична величина, що визначає розмір поверхні, одна з основних властивостей геометричних фігур, у математиці розглядається як міра множини точок, які займають поверхню або якусь її частину. Площа та її властивостірівні фігури мають рівні площі; якщо фігура розбивається на частини, кожна з яких є простою фігурою, то площа всієї фігури дорівнює сумі площ її частин площа квадрата зі стороною, яка дорівнює одиниці вимірювання, дорівнює одиниці. Площа квадрата зі стороною 1 мм, 1 см, 1 дм, 1 м відповідно дорівнює 1 мм2 , 1 см2 , 1 дм2 , 1 м2 Властивості:

Одиниці вимірювання площ

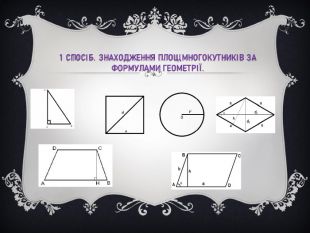
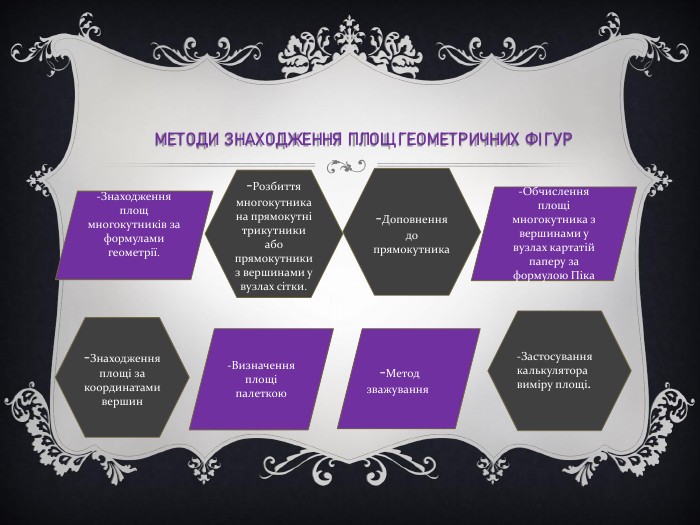
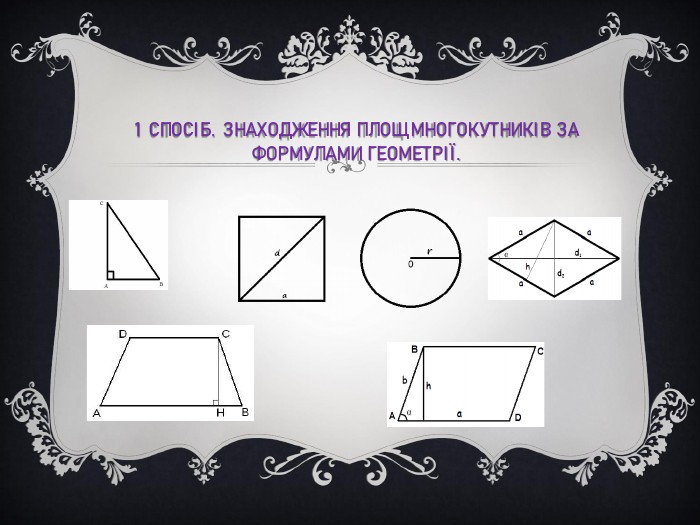
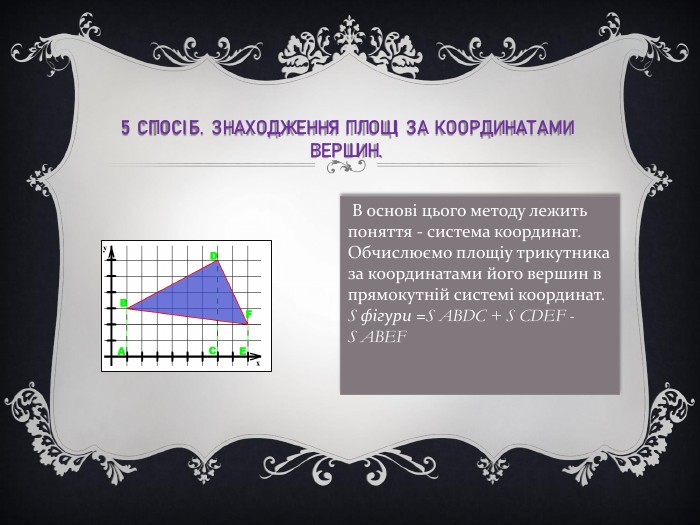
Методи Знаходження площ геометричних фігур-Знаходження площ многокутників за формулами геометрії.-Розбиття многокутника на прямокутні трикутники або прямокутники з вершинами у вузлах сітки.-Доповнення до прямокутника-Обчислення площі многокутника з вершинами у вузлах картатій паперу за формулою Піка-Знаходження площі за координатами вершин -Визначення площі палеткою -Метод зважування -Застосування калькулятора виміру площі.

1 спосіб. Знаходження площ многокутників за формулами геометрії.

2спосіб. Розбиття многокутника на прямокутні трикутники або прямокутники з вершинами у вузлах сітки. - Зміст даного способу полягає в тому, що многокутник розрізається на прямокутники або прямокутні трикутники з вершинами у вузлах сітки

3спосіб. Доповнення до прямокутника.-Зміст даного способу - це доповнення многокутника до прямокутника, а потім віднімання зайвих частин.

4спосіб. Обчислення площі многокутника з вершинами у вузлах картатій паперу за формулою Піка Знаходження площі багатокутника за формулою Піка, де вузол - перетин двох прямих,

5 спосіб. Знаходження площі за координатами вершин. В основі цього методу лежить поняття - система координат. Обчислюємо площіу трикутника за координатами його вершин в прямокутній системі координат. S фігури =S ABDC + S CDEF -S ABEF 

6 спосіб. Визначення площі палеткою Квадратну палетку накладають на контур ділянки й підраховують кількість повних квадратів, що вміщуються в ньому. Частки неповних квадратів по периферії ділянки підраховують "на око", доповнюючи їх до цілих квадратів

7 спосіб. Метод зважування Полягає в вибіру допоміжної величини. Потрібно нанести на щільний папір квадрат, площа якого S1 точно відома, вирізати його та визначити на терезах його масу m1. На такий самий папір перенести фігуру з площею S, що знаходиться. Вирізати фігуру і визначте її масу m. Потім, користуючись правилом пропорції – S/S 1 = m/m1,та обчислити шукану площу.

8спосіб. Застосування калькулятора виміру площіДля даного методу необхідно знайти в Інтернеті гул карту і ввести по контуру фігури координати. Тоді даний калькулятор знаходить площу.

Спочатку дані методи розглянули на опуклих та неопуклих многокутниках 1 спосіб (за формулами геометрії, розбиття та доповнення до прямокутника): S = Sкв - (S Δ АFB + S Δ BJC + S Δ CKD + S Δ DIE + S Δ AGE + S Δ АGHF )S = 64 – (4+3+6 +5+3+4) =31 (см2) 2 спосіб (за формулою Піка): S = 6/2 +29 -1= 31 (см2) Відповідь: 31 см 23 спосіб (за палеткою)S = 19+24/2= 19+12= 31 (см2) Обчислюючи площу опуклого многокутника різними способами, отримали один і той самий результат. S ABCD= S AEFL - (S Δ АEB + S Δ AHD + S MGCL + ) =24-17,5=6,5 (см 2)За формулою Піка S ABCD=5+5/2 -1=6,5 (см 2)Відповідь: 6,5 см 2 За допомогою палетки: S ABCD=1+11/2 =6,5 (см 2)І знову отримали один і той самий результат.

Обчислення площі круглих тіл. Обчислемо площу кільця за допомогою палетки а також застосуємо формулу Піка і порівняємо отриманий результат з результатом , отриманим використовуючи формулу для обчислення площі кола (мал.10). За допомогою формули Піка: В = 32, Г = 8, S = 32 + 4 - 1 = 35( см 2)Мал.10. Площа круглого тіла. S = πR2 S = 3 * 16 - 3 * 4 = 48 - 12 = 36 (см2) Округлимо тепер π до десятих: S = πR2 - πr2 = 3,1 * 16 - 3,1 * 4 = 49,6 - 12,4 = 37,2 (см2) А якщо округлити число π до сотих, то отримаємо: S = πR2 - πr2 = 3,14 * 16 - 3,14 * 4 = 50, 24 - 12,56 = 37,68 ( см 2)

Карачунівський гранітний кар’єр

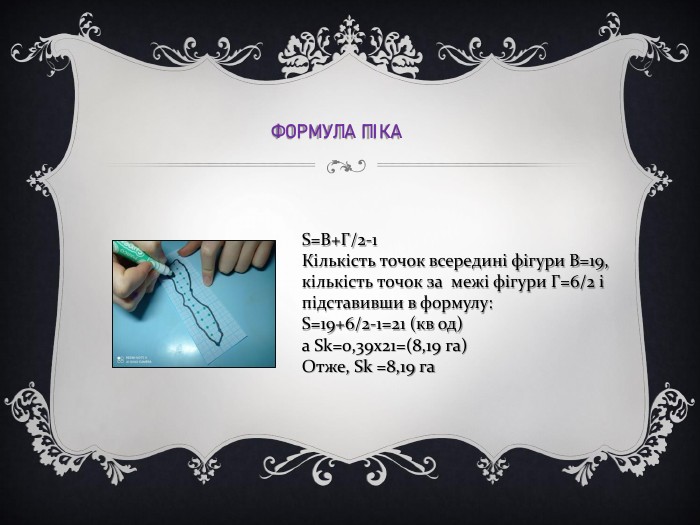
Застосування калькулятора виміру площі. Довжина поділки палетки 1см враховуючи масштаб карти маємо: 1,6см-100м 1см-х м Х= (1х100)/1,6 Х =62,5 м Знаходимо площу однієї поділки палетки, яка відповідає дійсній величині на місцевості: Sn= 62,5х62,5=0,39 (га), Sn- площа однієї палетки. S=8,3га. Масштаб 1,6см:100м

Метод Палетки. Використовуємо палетку (міліметровий папір). Кількість повних квадратів n1=9, неповних n2=12. Та користуємося формулою Sk=0,39 х N, Sk – площа кар’єру N=9+12=21 Sk=0.39х21=8,19 (га)Таким чином Sk=8,19 га

Метод зважуванняmd=0,06г та еталону me=0.003г. Sk : Sе= md : me Sе= Sn. Sk : 0,39= 0,06 : 0,003 Sk =(0,06х0,39)/0,003=7,8 (га)Як бачимо, цей спосіб не дуже точний, але й його можна застосовувати в крайніх випадках. Отже , Sk =7,8 га

Формула Піка. S=B+Г/2-1 Кількість точок всередині фігури В=19, кількість точок за межі фігури Г=6/2 і підставивши в формулу: S=19+6/2-1=21 (кв од)а Sk=0,39х21=(8,19 га)Отже, Sk =8,19 га

Метод доповнення до прямокутника. Sпр=3см х 12,6см =37,8 (см2 )S1= (0,9х0,7)/2=0,315 (см2 )S2=(0,4х3,2) =1,28(см2 )S3=0,4 х 3,7 = 1,48(см2 )S4=(1,1х1,1)= 1,21(см2 )S5=(1,1х2,8)/2=1,54(см2 )S6= (2,9 х0,5)/2=0,725(см2 )S7=2,7х0,7/2 = 0,98(см2 )S8=( 2х0,5)/2= 0,5 (см2 )S9=0,6х2= 1,2 (см2 )S10= 0,8х2,5= 2(см2 )S11=(0,8+0,4)/2х1,5= 0,9(см2 )S12=2х0,8= 1,6(см2 ) S13=1х1= 1(см2 )S14=2,3х1,3/2=1,495(см2 )S=0,315+1,28+1,48+1,21+1,54+0,725+0,98+0,5+1,2+0,5+2+0,9+1,6+1+1,495=16,225(см2 )Sп=37,8-16,225=21,575(см2 ) Sk = 21,575х0,39=8,41425≈8,4(га)За даним методом Sk =8,4 га 

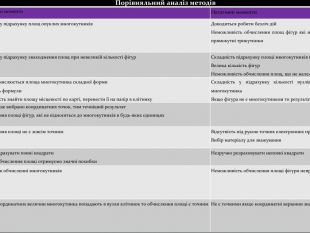
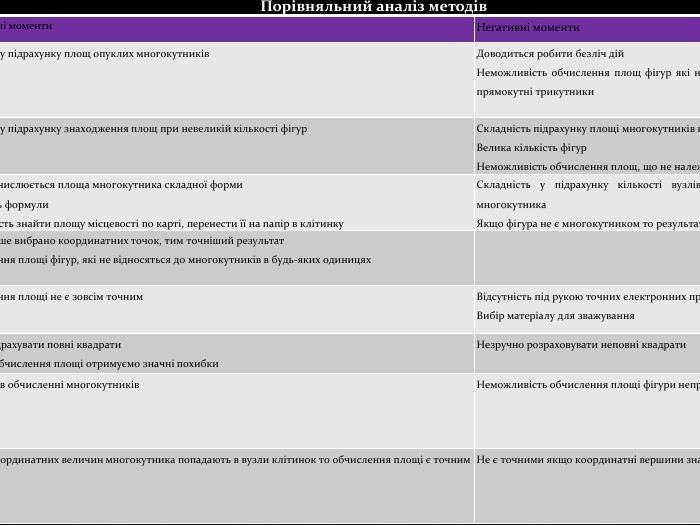
{073 A0 DAA-6 AF3-43 AB-8588-CEC1 D06 C72 B9}Порівняльний аналіз методів Метод. Позитивні моменти. Негативні моменти1 Метод розбиття на прямокутники та прямокутні трикутники. Простий у підрахунку площ опуклих многокутників. Доводиться робити безліч дій. Неможливість обчислення площ фігур які не розбиваються на прямокутники або прямокутні трикутники2 Метод доповнення до прямокутника. Простий у підрахунку знаходження площ при невеликій кількості фігур. Складність підрахунку площі многокутників незвичної форми. Велика кількість фігур. Неможливість обчислення площ, що не належать до многокутника3 Формула Піка. Легко обчислюється площа многокутника складної форми. Стислість формули. Можливість знайти площу місцевості по карті, перенести її на папір в клітинку. Складність у підрахунку кількості вузлів, що лежать близько до сторони многокутника. Якщо фігура не є многокутником то результат знаходження площ не точний4 За допомогою онлайн калькулятора. Чим більше вибрано координатних точок, тим точніший результат. Обчислення площі фігур, які не відносяться до многокутників в будь-яких одиницях 5 Метод зважування. Обчислення площі не є зовсім точним. Відсутність під рукою точних електронних пристроїв. Вибір матеріалу для зважування6 Метод палетки. Легко підрахувати повні квадрати. Під час обчислення площі отримуємо значні похибки. Незручно розраховувати неповні квадрати7 Знаходження площ за формулами геометріїТочність в обчисленні многокутників. Неможливість обчислення площі фігури неправильної форми8 Знаходження площ за координатними величинами. Площі координатних величин многокутника попадають в вузли клітинок то обчислення площі є точним. Не є точними якщо координатні вершини знаходяться не в вузлах

Висновок В результаті дослідження гіпотеза про те, що будь яку площу фігури, якщо вона перенесена на папір в клітинку, можна легко виміряти і обчислити різними методами з достатньою точністю, підтвердилась. Виконавши роботу, прийшли до висновків:1) велика кількість формул та методів обчислення площ належить вченим Евкліду, Архімеду, Піфагору, П. Ферма, Г. Піку та іншим [ 7];2) для обчислення площ фігур можна скористатися формулами геометрії, доповнення до прямокутника, формулою Піка, за палеткою, розбиттям на прямокутники та прямокутні трикутники, методом зважування , застосування калькулятора виміру площ ; 3) порівнявши різні способи знаходження площі опуклих та не опуклих многокутників прийшли до висновку, що зручними та доцільними і легкими є метод Піка та метод доповнення до прямокутника;

4) досліджуючи площу Карачунівського гранітного кар’єру, застосували методи знаходження площі опуклих, не опуклих многокутників, можливо обчислити наближене значення площі місцевості по карті, якщо перенести макет об’єкту на міліметровий папір;5) визначена площа Карачунівського гранітного кар’єру онлайн калькулятором становить - 8,3 га ; результати, отримані різними методами не співпадають, але близькі та похибка не значна;Вибір методу обчислення площ фігур залежить від форми фігури. 6.) розглянуті методи знаходження площ мають практичний інтерес і можуть використовуватися як для розв’язання задач так і застосування в житті для практичної діяльності.   

Дякую за увагу!