Презентація до позакласного заходу з математики "Криптоарифметичні задачі"

“Криптоарифметичні задачі”

План1) Вступ 2)Поняття криптографічних задач та їх види.3)Приклади математичних ребусів на дію додавання та множення:4)записаних буквами5)записаних за допомогою знаків та чисел6)зображених за допомогою геометричних фігур7)Висновки 8)Використана література

Моя думкаІнколи можна почути думку, що математика є сухою та нудною наукою. Я не погоджуюся, адже в ній є багато цікавого, нерозгаданого, нового, такого, що привертає увагу та захоплює. Серед численних математичних задач, вправ, виразів, кросвордів виділяють не менш цікаві математичні ребуси. В математиці їх ще називають криптоарифметичними задачами. Такі задачі привернули мою увагу та стали предметом мого дослідження.

Математичні ребуси. Математичні ребуси – це завдання, в яких треба відновити записи окремих математичних дій (наприклад, додавання, множення, ділення, добування квадратного кореня) або кількох послідовних. Здебільшого цифри у ребусах зашифровано буквами, значками або геометричними фігурами. Розв’язування криптоарифметичних задач – прекрасна гімнастика для розуму. Саме тому мені спало на думку дізнатися більше про такі вправи, навчитися їх вправно розв’язувати, а також складати власні математичні ребуси.

Типи криптоарифметичних задач. Криптоарифметичні задачі можуть бути записані : За допомогою геометричних фігур;За допомогою букв;За допомогою значків, де частково записано числа. Кожна буква або фігура в умові означає лише одну цифру, а різні букви або фігури – різні цифри. Відновлювати цифри у задачах потрібно на основі правильно побудованих ланцюжків логічних міркувань. Інколи математичні ребуси мають кілька варіантів розв’язків. Правильний шлях до розв’язування ребусу з математики – це перевірка всіх можливих варіантів, які слід перевіряти безпосереднім випробуванням.

Буквені ребуси. Розглянемо приклад математичного ребусу, записаного буквами: к н и г а + к н и г а к н и г а н а у к а Для того щоб розв’язати дану вправу слід міркувати так : з п’ятого стовпця видно, що “а” дорівнює 0 або 5. Якщо “а”= 0, то з третього стовпця видно, що “н” дорівнює 3 або 6 . Але тоді в цьому стовпці є перехід через десяток і не можна узгодити числа у першому стовпці. Виходить “а”- не 0. Якщо “а” = 5, то “н” = 8. Тоді в першому стовпці “к” = 2. Підставивши це значення к у четвертий стовпець, бачимо, що “г”= 7. Випробовуючи значення “и”, пересвідчуємось, що в третьому стовпці тільки при “и”= 3, “у”= 1 дістанемо правильний запис. Отже, математичний ребус розв’язаний: 2 8 3 7 5 + 2 8 3 7 5 2 8 3 7 5 8 5 1 2 5

Лінійні ребуси. Серед математичних ребусів можна виділити лінійні. Щоб їх розв’язати потрібно підібрати числа так, щоб вони задовольняли умови. Наприклад:1)Л+Л=АД, а Л*Л=ДА (9+9=18 і 9*9=81)2)АМ+І=АК, а АМ*І=КА (24+3=27 і 24*3=72)3)ОР+І=ОН, а ОР*І=НО (47+2=49 і 47*2=94)4)МОН: ОН=5 (125:25=5 або 375:75=5)5)ЧАЙ: АЙ=25 (625:25=25).

Криптоарифметичні задачі на дію додавання. Розглянемо приклади деяких криптоарифметичних задач на дію додавання. Т Р И + О Д И Н О Д И Н П’Я Т Ь ( Розв’язок : 512+4623+4623=9758. Отже, “и”= 2, “р”= 1, “т”=5, “д”=6, “о”=4, “н”=3, “п”=9, “я”=7, “ь”=8)

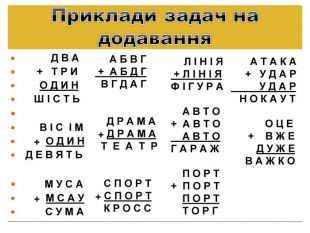
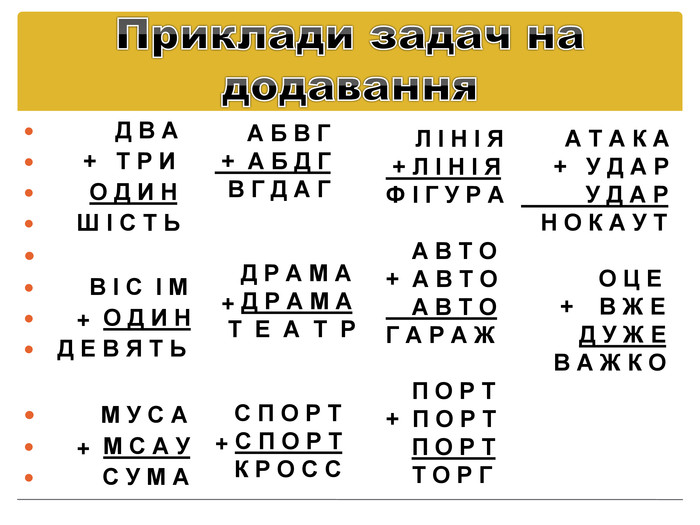
Приклади задач на додавання Д В А + Т Р И О Д И Н Ш І С Т Ь В І С І М + О Д И Н Д Е В Я Т Ь М У С А + М С А У С У М А А Б В Г + А Б Д Г В Г Д А Г Д Р А М А + Д Р А М А Т Е А Т Р С П О Р Т+ С П О Р Т К Р О С С Л І Н І Я + Л І Н І ЯФ І Г У Р А А В Т О+ А В Т О А В Т ОГ А Р А Ж П О Р Т+ П О Р Т П О Р Т Т О Р Г А Т А К А + У Д А Р У Д А Р Н О К А У Т О Ц Е + В Ж Е Д У Ж Е В А Ж К О

Цікавий ребус 9 3 2 +9 3 3 8___________ 1 0 2 7 0

Цікавий ребус. Оригінальним є математичний ребус складений із прислів’я «Куда голка, туда нитка»: К У Д А + Г О Л К А Т У Д А Н И Т К А

Інші ребуси. Розглянемо наступні математичний ребуси1)ДІМ+ДІМ+ДІМ+ДІМ+ДІМ+ДІМ=ДВІР (“д”= 1, “в”= 0, “о”= 7 або 8, таким чином 179*6 = 1074)2)РІК+РІК+РІК+РІК+РІК+РІК=РОКИ (“р”=1, і більше,або дорівнює 6, таким чином 173*6 = 1038)3)СЛОВО+СЛОВО+СЛОВО+СЛОВО+СЛОВО+СЛОВО+СЛОВО=ФРАЗА (“С”=1, “О“– не 0 і не 5, “О”=6, тоді 13606*7=95242)

Знакові та числеві ребуси. Прикладом математичного ребусу є також ребус записаний за допомогою знаків та чисел: **+ ***8 ** 99+** +99*98 198

Точкові задачіУ наступному математичному ребусі однакові букви відповідають однаковим числам, а різні букви – різним числам; точки можуть бути різними числами.406*406+24360001624164836

Криптоарифметичні телеграми. За допомогою криптографічних задач можна записувати телеграми. У поданому тексті телеграми останнє слово має означати число, яке дорівнює сумі чисел, зашифрованих іншими словами тексту. Зміст цієї телеграми НІНІ ТАНІ ГРИНІ ПРИВІТ, можна розшифрувати таким способом (5656+8256+90456=104368)

Дія множення у ребусах. У математичних ребусах може бути використана і дія множення, наприклад : Р Е Б У С * РС С С С С С Б Е Е Е * БМ У У У(3222*3=9666)   В Н К *Б 2 Б В Н К +Б В 7 С В 8 КБ Б В С 2 К

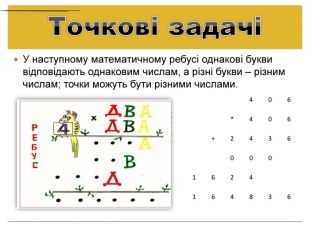
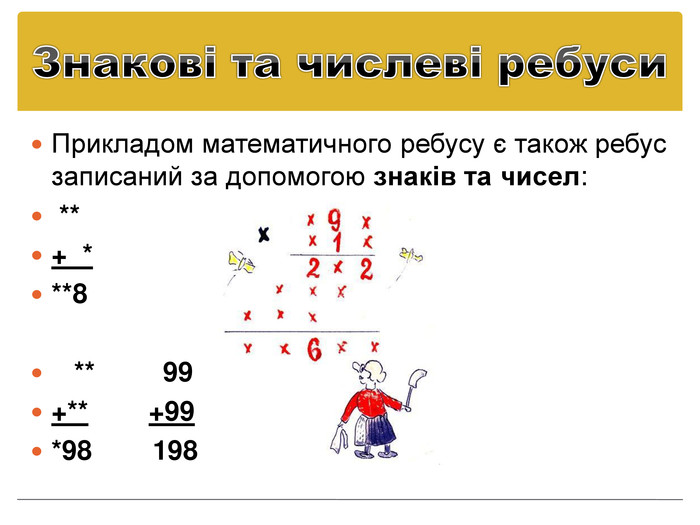
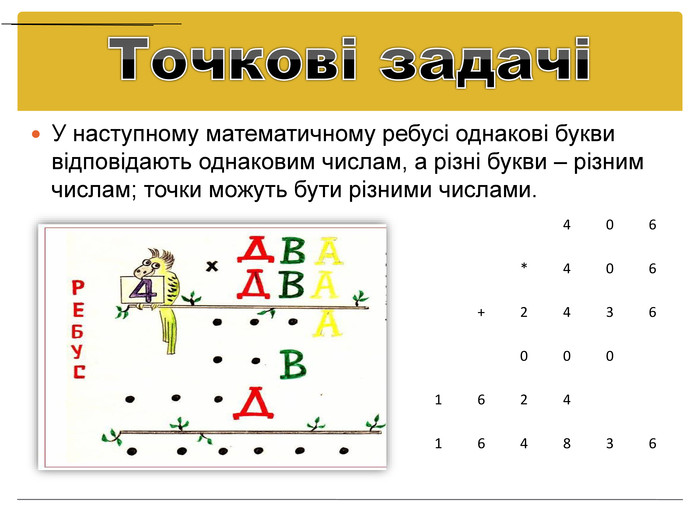
Добутки чисел, що зашифровані геометричними фігурами. Розглянемо такі добутки чисел, що зашифровані геометричними фігурами: * + Розв’язуючи цю криптографічну задачу, зі стовпця десятків видно, що більший за . Оскільки, добуток * закінчується (причому не дорівнює 1 та не дорівнює 0), то або = 5 і - непарна цифра, або = 6 і - парна цифра. Таким чином це добуток 75*77=5775.

Мої власні ребуси. Дізнавшись багато нового про криптографічні задачі, мені вдалося скласти власні ребуси. У нище наведених математичних ребусах під зірочками зашифровано парні цифри. Спробуємо їх розв’язати: 6(оскільки, при додаванні переходу нема, бо усі числа є парними, то перша цифра другого добутку 6. Отже, перші цифри множників – 8 і 8, бо 8*8=64. Другі цифри 0 і 6. Тоді множники 80*86=6880)

Мої приклади *+ 8( стовпець десятків складається з 2+6, або 4+4, або 6+2, або 8+0. Провівши випробовування можна зробити висновок, що придатний лише останній варіант, отже зашифрований добуток 60*48=2880 )

Висновок. Серед математичних ребусів є багато записаних у різних системах числення, наприклад, двійкові, трійкові, шісткові системи та інші. У цій роботі, наведені мною криптоарифметичні задачі усі подані в добре знайомій нам десятковій системі числення. Я планую в подальшому допрацювати свою роботу і включити в неї математичні ребуси зашифровані у різних системах числення. Криптоарифметичні задачі - цікаві, захоплюють своєю оригінальністю та різноманітністю як способом записування , так і тематикою різних зашифрованих слів, висловів, чисел. Такі вправи сприяють розвитку логічного мислення, змушують проявляти індивідуальну творчість. А ще підвищують інтерес до вивчення складного навчального предмету – математики.  

Використана література1) “У світі математики”. Випуск 17,Радянська школа, 1986.-224с..2) “Математика після уроків”. Тернопіль: Мандрівець, 2007.-88с..3) “Цікаві задачі”. М. Савченко