Презентація до уроку алгебри 11 класу «Найбільше і найменше значення функції на відрізку. Прикладні задачі на знаходження найбільшого і найменшого значень.»
Про матеріал
Презентація до уроку алгебри 11 класу «Найбільше і найменше значення функції на відрізку. Прикладні задачі на знаходження найбільшого і найменшого значень.»
Мета уроку:
- ознайомити учнів зі змістом понять « найбільше значення функції на відрізку» і «найменше значення функції на відрізку»;
- сформулювати алгоритм знаходження найбільшого й найменшого значення функції на відрізку;
- формувати вміння і навички застосовувати його при розв'язуванні вправ;
- формувати уявлення про математику як форму опису і метод пізнання дійсності.
Розвивати комунікативні та інформаційні компетентності, компетентності саморозвитку і самоосвіти та продуктивної творчої діяльності.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра (академічний, профільний рівень) 11 клас (Нелін Є.П., Долгова О.Є.)
До уроку
5.3. Найбільше і найменше значення функції Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




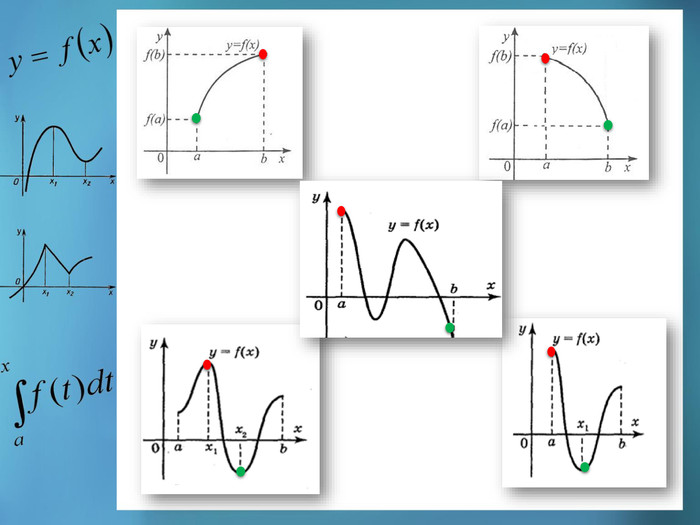
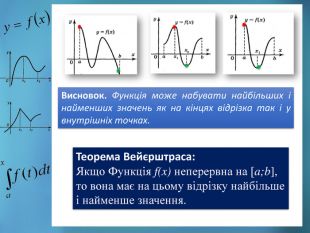
![Висновок. Функція може набувати найбільших і найменших значень як на кінцях відрізка так і у внутрішніх точках. Теорема Вейєрштраса: Якщо Функція f(x) неперервна на [a;b], то вона має на цьому відрізку найбільше і найменше значення. Висновок. Функція може набувати найбільших і найменших значень як на кінцях відрізка так і у внутрішніх точках. Теорема Вейєрштраса: Якщо Функція f(x) неперервна на [a;b], то вона має на цьому відрізку найбільше і найменше значення.](/uploads/files/54441/36440/37109_images/6.jpg)
![Алгоритми знаходження найбільших і найменших значень. Знайти стаціонарні точки функції на [a; b];Обчислити значення функції в стаціонарних точках;Обчислити значення функції в точках a і b(на кінцях відрізку);Вибрати найбільше і найменше значення функції серед усіх знайдених. Алгоритми знаходження найбільших і найменших значень. Знайти стаціонарні точки функції на [a; b];Обчислити значення функції в стаціонарних точках;Обчислити значення функції в точках a і b(на кінцях відрізку);Вибрати найбільше і найменше значення функції серед усіх знайдених.](/uploads/files/54441/36440/37109_images/7.jpg)
![Виконання вправ1. Знайти найбільше і найменше значення функції у = f(x) на вказаному проміжку.а) у(х) = 3х2 - х3; [-1; 3]; б) у(х) = 2х3 + 3х2 – 12х + 1; [0; 3]. Відповідь:a) fнайб.= 4; f найм = 0;б) fнайб.= 46; f найм = -6. Виконання вправ1. Знайти найбільше і найменше значення функції у = f(x) на вказаному проміжку.а) у(х) = 3х2 - х3; [-1; 3]; б) у(х) = 2х3 + 3х2 – 12х + 1; [0; 3]. Відповідь:a) fнайб.= 4; f найм = 0;б) fнайб.= 46; f найм = -6.](/uploads/files/54441/36440/37109_images/8.jpg)
![2. Знайти найбільше і найменше значення функціїї в) у=х³-1,5х²-6х+1 на проміжку [-2;0]г) у= Х4 -8х²+3 на проміжку [-2;2]Виконання вправ3. Доведіть, що функція спадає на множині дійсних чисел.𝑦=−13𝑥3+12𝑥2+12 2. Знайти найбільше і найменше значення функціїї в) у=х³-1,5х²-6х+1 на проміжку [-2;0]г) у= Х4 -8х²+3 на проміжку [-2;2]Виконання вправ3. Доведіть, що функція спадає на множині дійсних чисел.𝑦=−13𝑥3+12𝑥2+12](/uploads/files/54441/36440/37109_images/9.jpg)


![Завдання № 1. Знайти різницю найбільшого та найменшого значення функції: f(x)=x2 + (16-x)2 на проміжку [8;16]№2. Рекламний бікборд має форму прямокутника площею 9м2. Як його виготовити, щоб периметр був найменшим?№ 3. Ділянку, площею 294м2, потрібно поділити на дві рівні частини огорожею так, щоб довжина огорожі була найменшою.↘↗ Завдання № 1. Знайти різницю найбільшого та найменшого значення функції: f(x)=x2 + (16-x)2 на проміжку [8;16]№2. Рекламний бікборд має форму прямокутника площею 9м2. Як його виготовити, щоб периметр був найменшим?№ 3. Ділянку, площею 294м2, потрібно поділити на дві рівні частини огорожею так, щоб довжина огорожі була найменшою.↘↗](/uploads/files/54441/36440/37109_images/12.jpg)













-

Гороховець Ніна Іванівна
01.04.2022 в 15:58
Дякую,що поділились!!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горик Руслана Миколаївна
26.03.2022 в 19:53
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Бершеда Людмила Олександрівна
26.04.2021 в 22:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Рязанова Галина Яківна
22.05.2020 в 00:44
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Стефаник Алла Миколаївна
09.04.2020 в 14:24
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука