Презентація до уроку алгебри у 8 класі "Додавання та віднімання раціональних дробів з однаковими знаменниками"
Про матеріал
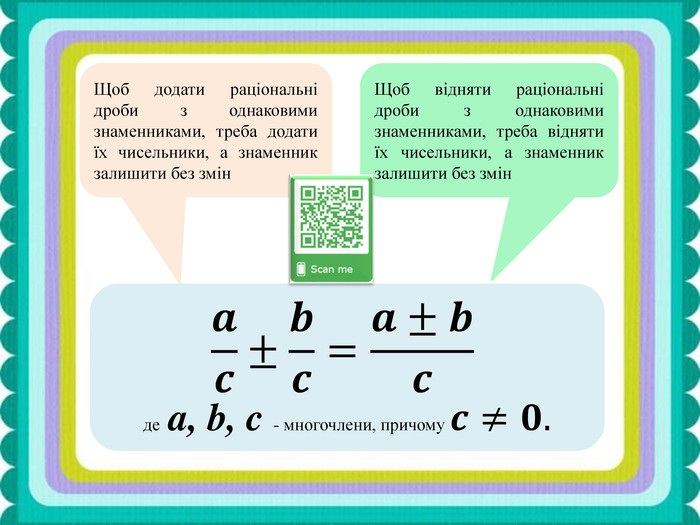
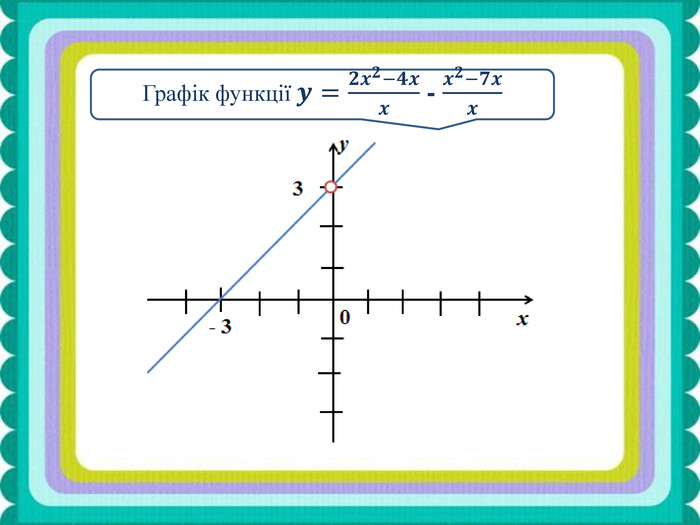
Презентація до уроку алгебри у 8 класі "Додавання та віднімання раціональних дробів з однаковими знаменниками" Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку























-

Білошапко Наталія Миколаївна
30.09.2024 в 22:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лесюк Ольга Семенівна
30.09.2024 в 09:05
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Джерело tkd94846
03.10.2023 в 22:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кушина Антоніна Василівна
25.09.2023 в 16:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
24.09.2023 в 21:19
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тимощук Оксана Феодосіївна
21.09.2023 в 20:47
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лашина Анастасія
08.03.2023 в 00:02
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Щербина Ольга
19.09.2022 в 18:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вагіна Оксана
04.11.2021 в 11:10
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 6 відгуків