Презентація до уроку геометрії "Теорема Піфагора"
Про матеріал
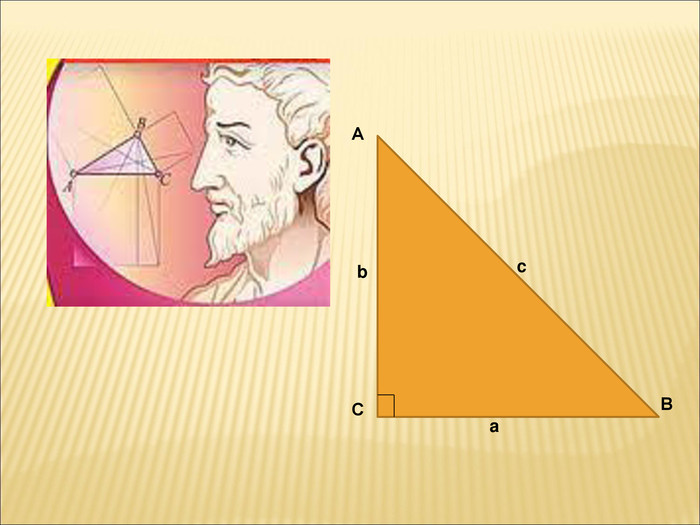
Сформулювати і довести теорему Піфагора;
познайомити учнів з біографією Піфагора;
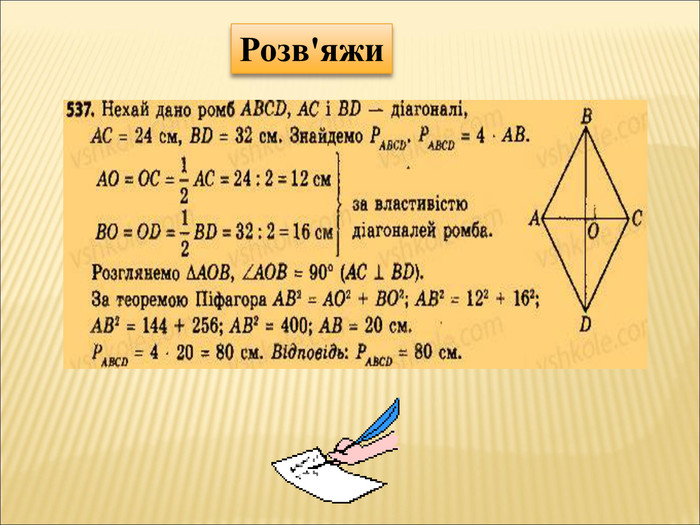
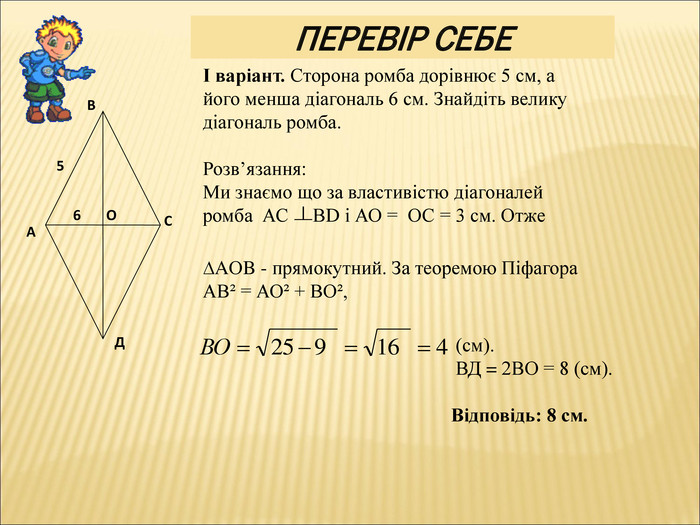
вчити застосовувати теорему до розв'язання задач;
розвивати логічне мислення;
розвивати інтерес до математики, вміння працювати в групі, парі.
Виховувати самостійність, толерантність, наполегливість у здобутті знань
Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку