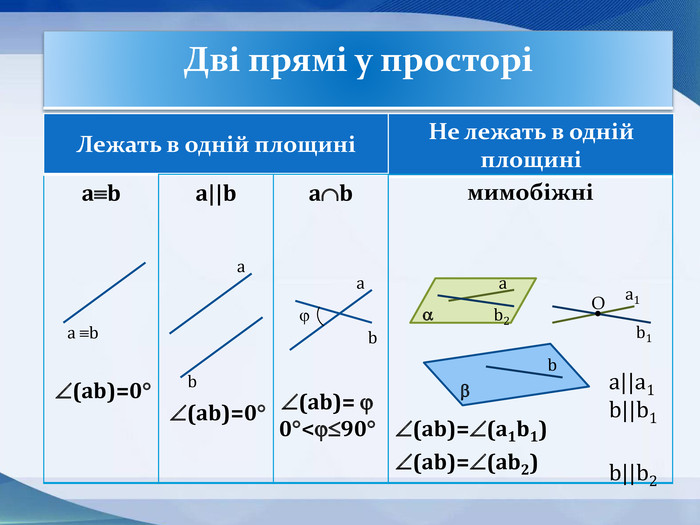
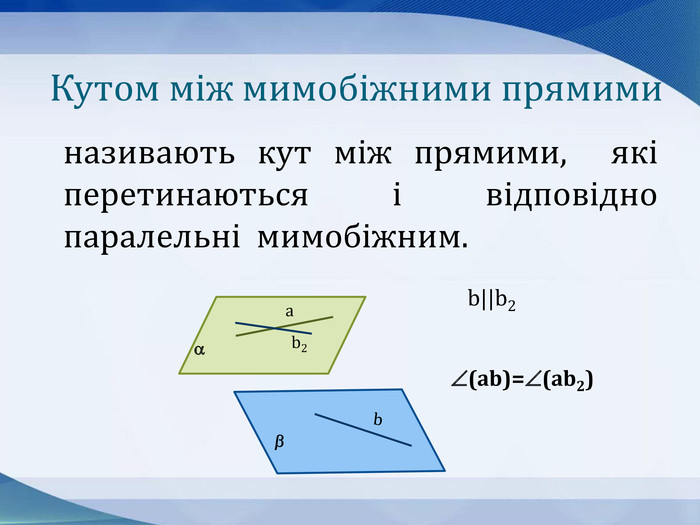
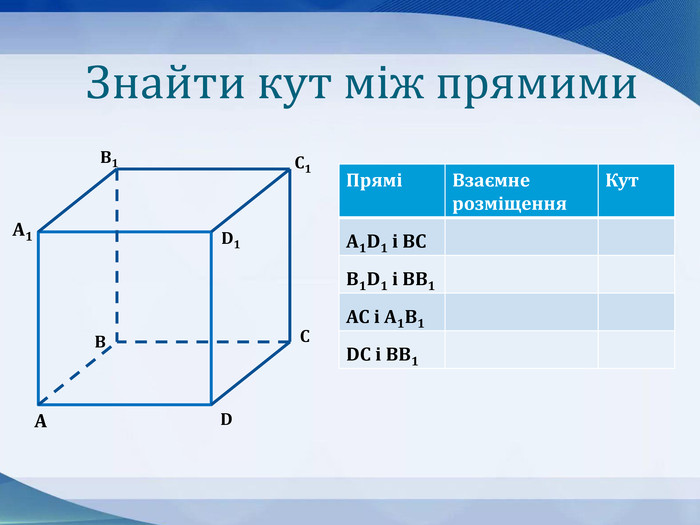
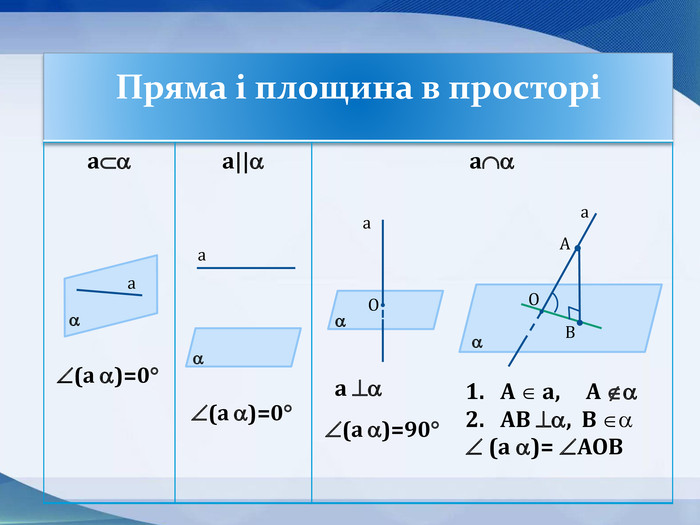
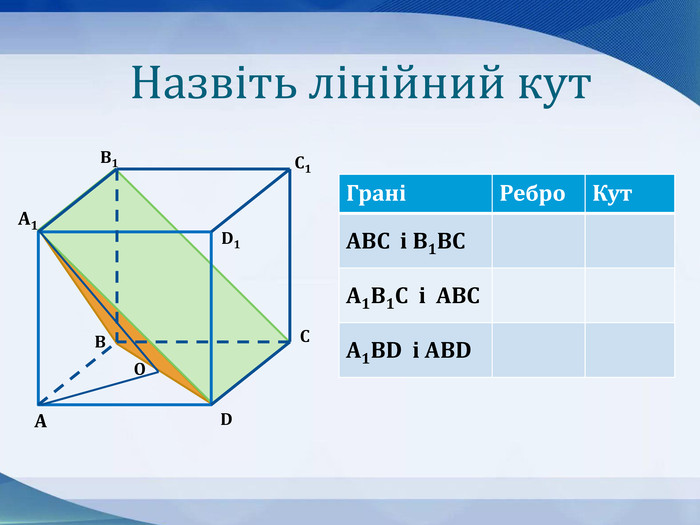
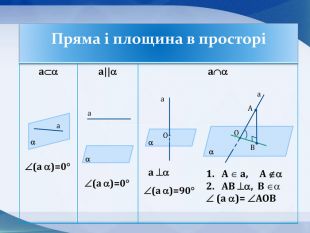
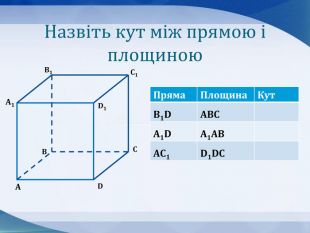
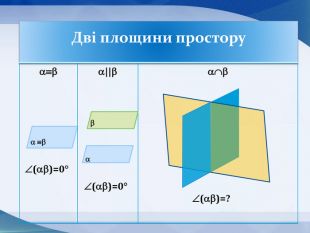
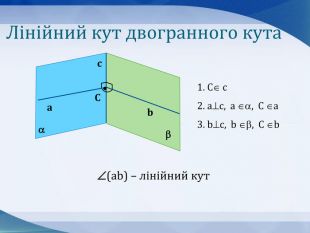
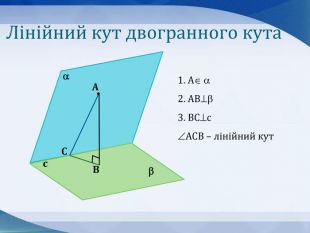
Презентація до уроку "Кути в просторі" 10 клас
Про матеріал
Дану презентацію можна використовувати для узагальнення та систематизації знань учнів або при підготовці до ЗНО для повторення навчального матеріалу з теми "Відстані та кути у просторі"; для закріплення вмінь розв`язувати задачі стереометрії з використанням різних прийомів. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку