Презентація до уроку "Логарифм та його властивості"
Про матеріал
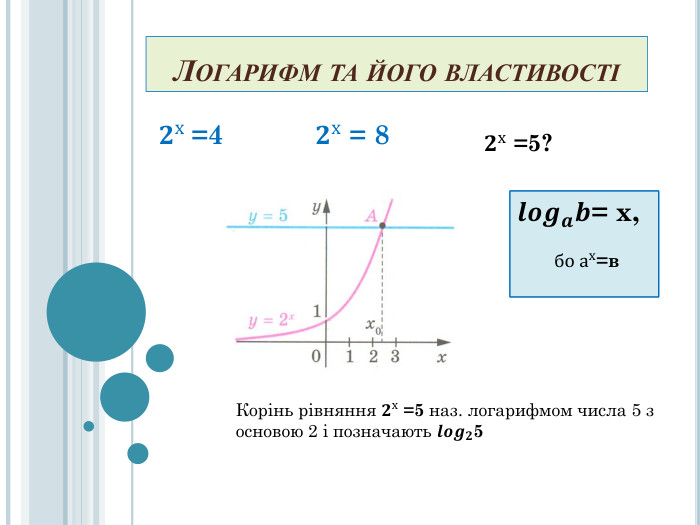
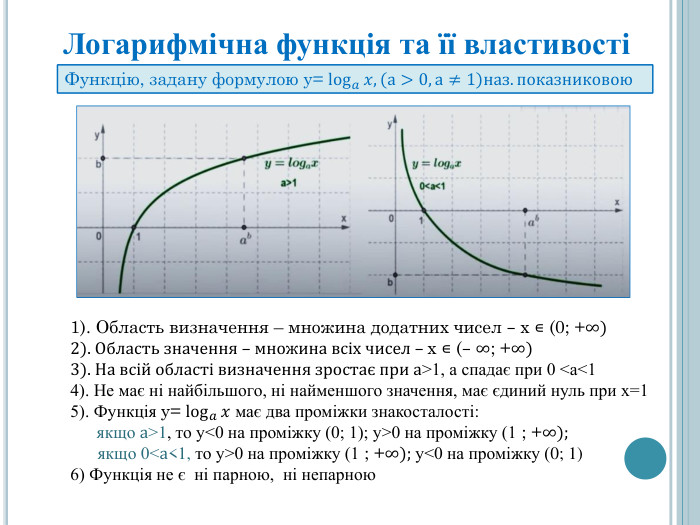
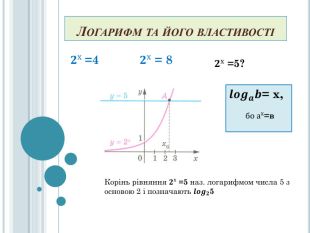
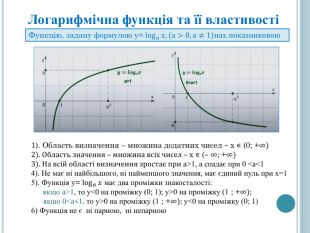
Формування поняття логарифма числа. Ознайомлення з основною логарифмічною тотожністю та властивостями логарифмів, логарифмічною функцією. Формувати вміння розв'язувати найпростіші вправи з логарифмами
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку