Презентація "Рівнобедрений трикутник 2"
Про матеріал
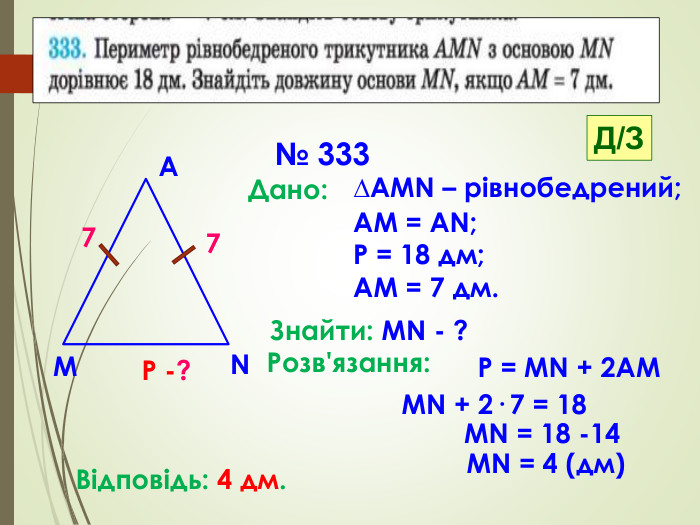
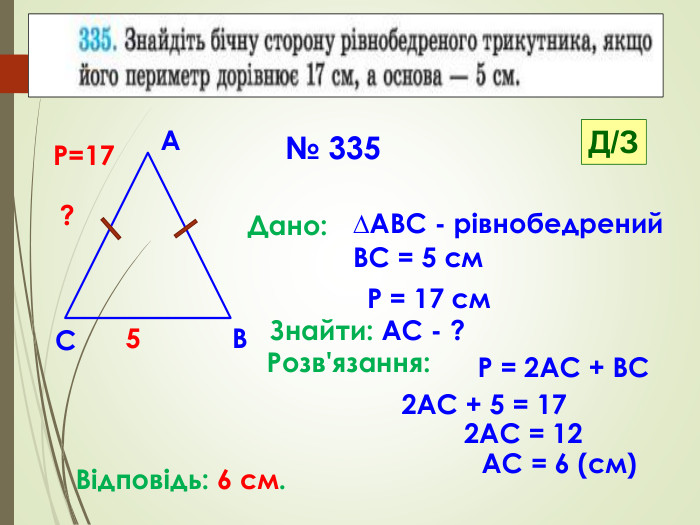
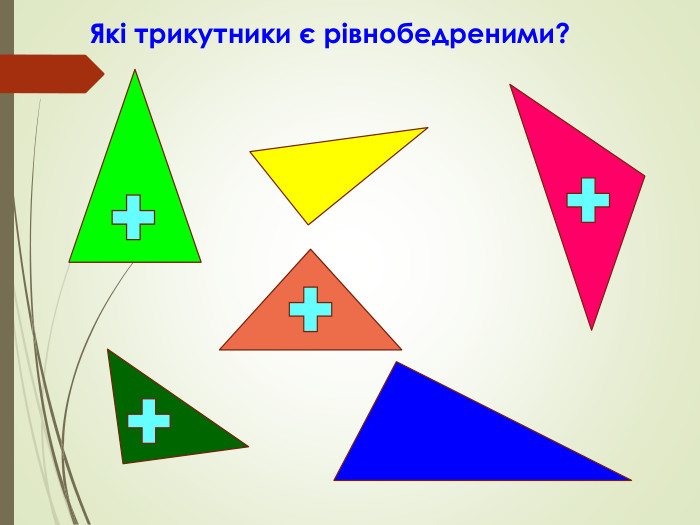
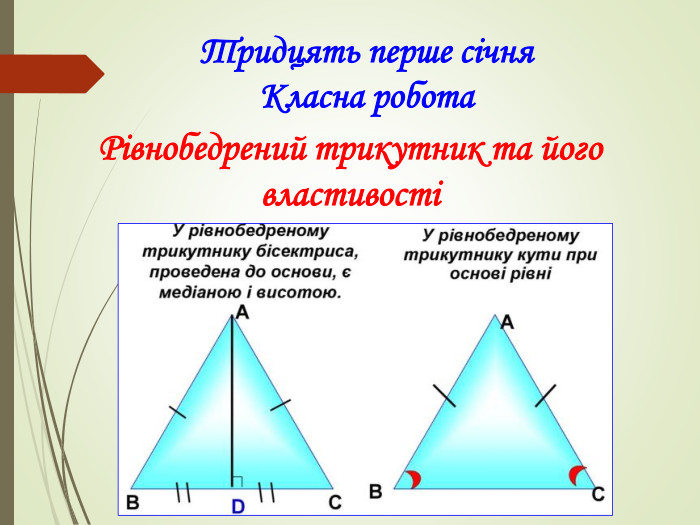
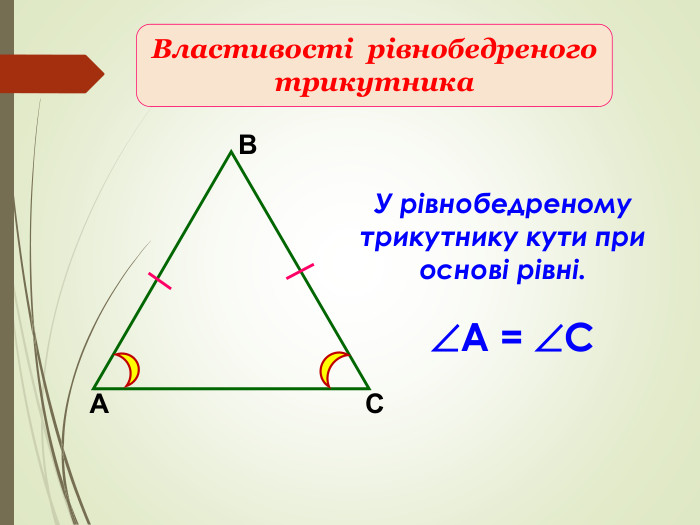
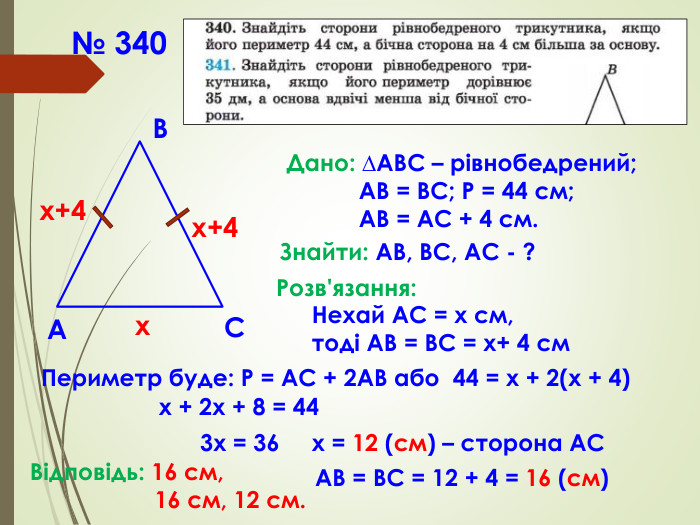
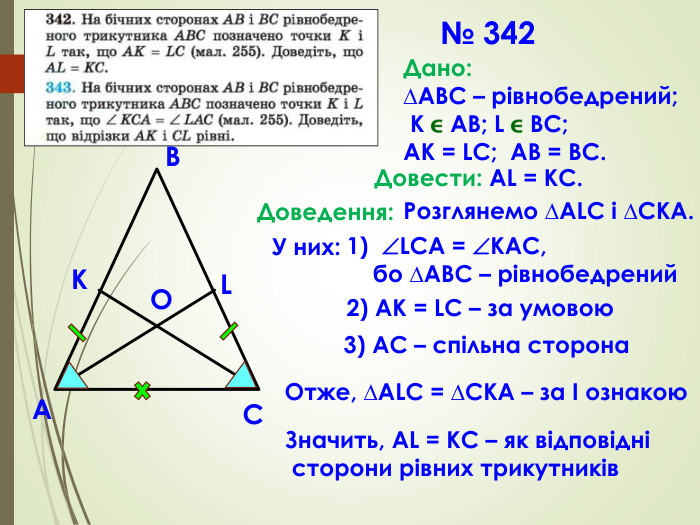
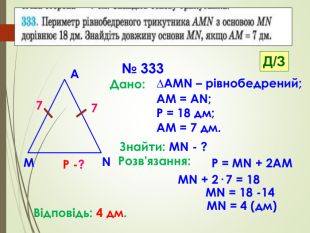
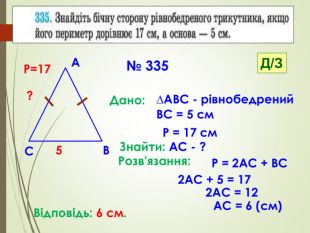
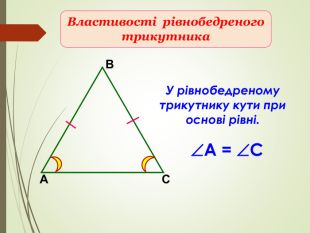
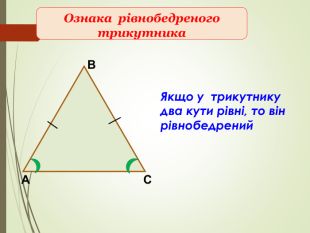
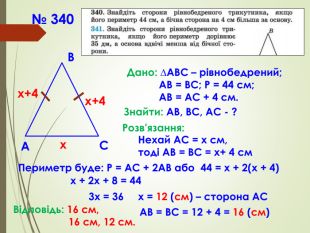
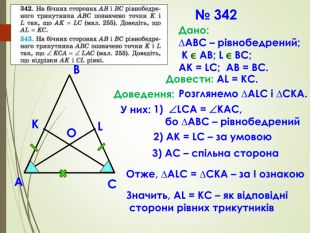
Презентація призначена для проведення уроку геометрії в дистанційному форматі у 7 класі за підручником О. С. Істер (2015 або 2018). Містить елементи анімації, що дуже зручно при проведені уроку вчителем і спілкуванні з дітьми. Матеріал підібраний у логічній послідовності. Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку