Презентація до уроку математики. 4 клас РОСТОК. З історії дробів
Про матеріал
Презентація до уроку математики в 4 класі за технологією "РОСТОК"
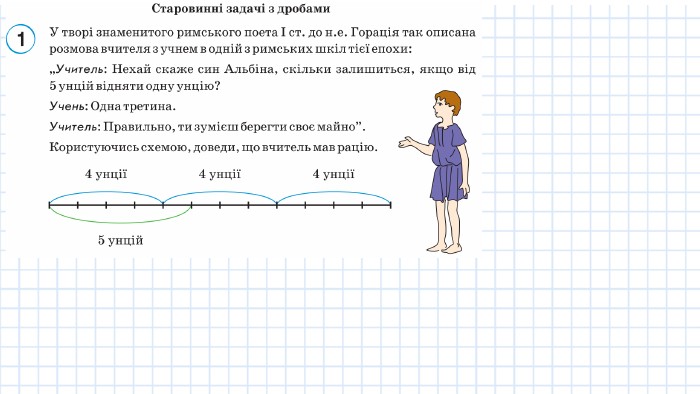
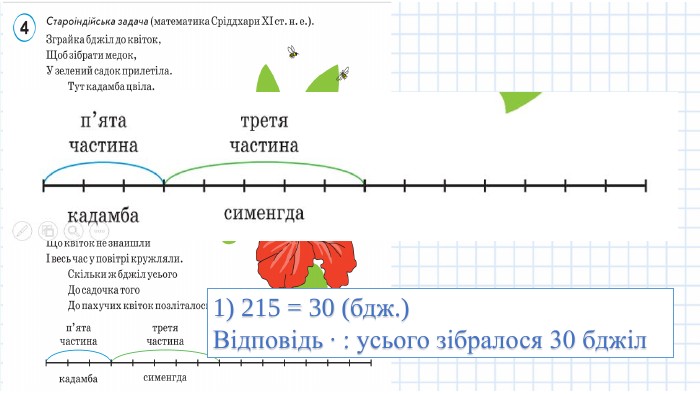
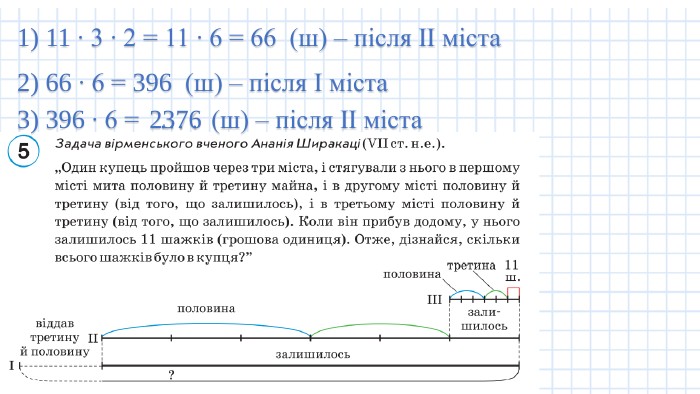
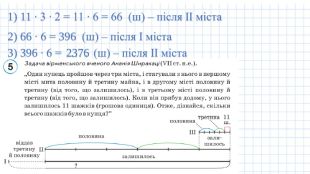
З історії дробів. Урок № 20, 2 частина
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку