Презентація до уроку математики в 6 класі з теми "Подільність чисел"

Подільність чисел 6 клас

Дільники – це ті числа на які ділиться дане число. Дільники числа 10 : 1; 2; 5; 10.10 : 1 = 1010 : 2 = 510 : 5 = 210 : 10 = 1

Перевір себе Чи правильно,що: а) 5 – дільник числа 35; б)18 – дільник числа 9;в) 13 – дільник числа 156?Назвіть дільники числа 32. Чи є для будь – якого числа найменші і найбільші дільники, які вони ?Знайдіть найменше число, дільниками якого є числа: 2, 5 і 11. Назвіть чотири найменших числа, дільниками яких є числа 8 і 6. 110;24;48;72; 96.2;4;1;8;16; 32;тактакніppt_xxshearppt_x

Ознаки подільності r

Якщо запис натурального числа закінчується на 0, то це число ділиться без остачі на 10. Якщо запис натурального числа закінчується будь-якою іншою цифрою, то воно не ділиться без остачі на 10.  Приклади:  680 ділиться на 10; 104 не ділиться на 10. 

Якщо запис натурального числа закінчується цифрами 0 або 5, то це число ділиться без остачі на 5. Якщо запис числа закінчується будь-якою іншою цифрою, то число не ділиться на 5 без остачі. Приклади: 370 і 1485 діляться без остачі на 5;числа 537 і 4008 без остачі на 5 не діляться. 

Якщо число закінчилось на 0,Або число закінчилось на 5,Про це всі учні мають знать: Число це ділиться на …( п'ять)

Як довідатись мені: Ділиться число на 2, чи ні?Щоб не помилитися,На останню цифру треба подивитися. Число на 2 поділиться в нас гарно,Якщо ця цифра.. парна

Із чисел 125,460,195,224,876,1540,7400,3048,5605,1380 випиши ті, які діляться: а) на 2 :б) на 5:в) на 10: 460; 224; 876;1540; 7400; 3048;1380;125; 460; 195; 1540; 7400; 5605;1380;460; 140;7400;1380.

Як довідатись мені - Ділиться число на 3, чи ні?Зробимо так я і ти : Суму цифр у числі треба знайти. Якщо сума поділиться на 3,То й число поділиться на 3

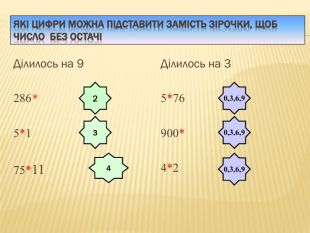
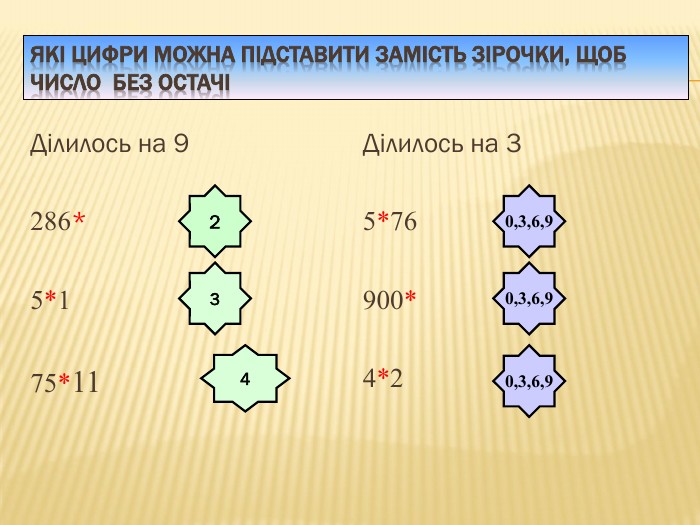
Якщо сума цифр числа ділиться на 3, то й саме число ділиться на 3. Якщо сума цифр числа не ділиться на 3, то й число не ділиться на 3. Приклади:276 ділиться на 3, оскільки 2 + 7 + 6 = 15, а 15 ділиться на 3; 563 не ділиться на 3, оскільки 5 + 6 + 3 = 14, а 14 не ділиться на 3.ppt_xxshearppt_xstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Якщо сума цифр числа ділиться на 9, то й саме число ділиться на 9. Якщосума цифр числа не ділиться на 9, то й число не ділиться на 9. Приклади:  5787 ділиться на 9, оскільки 5 + 7 + 8 + 7 = 27, а 27 ділиться на 9; 359 не ділиться на 9, оскільки 3 + 5 + 9 = 17, а 17 не ділиться на 9. ppt_xxshearppt_xstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Які цифри можна підставити замість зірочки, щоб число без остачіДілилось на 9286* 5*175*11 Ділилось на 3 5*76900*4*22430,3,6,90,3,6,90,3,6,9

Із цифр 0, 3, 4, 5 складіть : а) трицифрові числа, які діляться на 2 і 5 одночасно; 340, 430, 350, 530, 540, 450. б) двоцифрові числа, які діляться 3; 30, 45, 54. в) двоцифрові непарні числа; 43, 45, 53. г) числа, які діляться на 9. 45, 54, 450, 540, 504, 405. rrrr

Прості і складені числа

Натуральне число називають простим, якщо воно має два різні дільники:одиницю і саме це число. Число 17 має два дільники, значить, воно просте. Натуральне число називають складеним, якщо воно має більше двох дільників. Число 9 має три дільники (1, 3 і 9), значить, воно є складене.

Запам'ятай,це може пригодиться,Що не просте і не складне число – це…одиницяppt_xxshearppt_x

1 2 3 4 5 6 7 8 9 10 12 13 14 15 16 17 18 19 2021 22 23 24 25 26 27 28 29 30 Решето Ератосфена. Решето́ Ератосфе́на в математиці — простий стародавній алгоритм знаходження всіх простих чисел менших деякого цілого числа n, що був створений давньогрецьким математиком Ератосфеном. r

(простим)Якщо число два дільники лиш має,То зараз кожен з вас згадає,Що це число і я , і ти –Усі назвем його …

Розкладання натуральних чисел на прості множники

Розкласти складене число на прості множники означає записати дане число у вигляді добутку простих чисел . 108 2 420 10=2∙5 54 2 42 2 27 3 21 3 9 3 7 7 3 3 1 1 При будь-якому способі запису одержуємо один і той самий розклад, якщо не враховувати порядку розміщення множників. Приклади:  180 = 2•2•3•3•5;  1368 = 2•2•2•3•3•19.

Розкладіть на прості множники числа: 72, 450, 135, 245.7222233233554503335135577245

Знайдіть усі дільники чисел 98,216,2272 Дільники числа 98: 1; 2; 7; 14; 49; 98. Дільники числа 140: 1; 2; 4; 5; 7; 10; 14; 20; 28; 140. Дільники числа 216: 1; 2; 3; 4; 6; 9; 8; 27; 24; 36; 54; 72;108; 216.style.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Найбільший спільний дільник(НСД)

Для знаходження НСД двох чисел можна розкласти ці числа на прості множники і знайти добуток їх спільних множників. Приклади: а) Знайти НСД (6600; 6300):6600 = 2 • 2 • 2 • 3 • 5 • 5 • 11,6300 =2 • 2 • 3 • 3 • 5 • 5 • 7,НСД (6600; 6300) = 2 • 2 • 3 • 5 • 5 = 300; б) Знайти НСД (34 398; 1260; 6552):34 398 = 2 • 3 • 3 • 3 • 7 • 7 • 13,1260 = 2 • 2 • 3 • 3 • 5 • 7, 6552 = 2 • 2 • 2 • 3 • 3 • 7 • 13,НСД (34 398; 1260; 6552) = 2 • 3 • 3 • 7 = 126. 

Запам'ятай Якщо НСД(a,b)=1, то a і b взаємно прості числа. Приклади: 75 і 14 - взаємно прості числа, оскільки НСД (75; 14) = 1;20, 9 і 77 взаємно прості числа, оскільки НСД (20; 9; 77) = 1.style.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Найменше спільне кратне (НСК)

Кратні натурального числа Кратним натуральному числу а називають натуральне число, яке ділиться на а без остачі.  Приклади:для числа 18 кратними є числа: 18, 36, 54, 72, 90, 108, 126 і т.д.;для числа 7 кратними є числа: 7, 14, 21, 28, 35, 42, 49 і т.д.  Отже, треба запам'ятати:1) будь-яке число має нескінченну кількість кратних;2) найменшим кратним для числа є саме це число. 

Найменшим спільним кратним натуральних чисел а і b називають найменше натуральне число, яке кратне і а, і b.  Треба запам'ятати:1) якщо одне із двох натуральних чисел ділиться на друге число, то більше з цих двох чисел є їх найменшим спільним кратним;2) якщо два числа є взаємно простими, то найменше спільне кратне цих чисел дорівнює їх добутку. Приклади:  НСК (9; 18) = 18;НСК (2; 8; 16) = 16, оскільки 8 ділиться на 2, а 16 ділиться на 8;НСК (7; 10) = 70, оскільки 7 і 10 - взаємно прості числа. style.colorfillcolorfill.type

Щоб знайти найменше спільне кратне декількох натуральних чисел, треба:1)розкласти їх на прості множники;2) виписати множники, що входять у розклад (краще найдовший) одного з чисел;3) дописати до них ті множники, що є в розкладі інших чисел;4) знайти значення утвореного добутку. 

Знайдіть найменше спільне кратне чисел 34,51,68 Розв'язання342171715131717168 234 217 171 НСК(34,51,68)=2∙2∙17∙3 Відповідь: 204=204

Перевірте себе. НСК (20;70;15) =НСК (18;45)= НСК (30;40) =НСК (210;350) = 120904201050r

Свінтозельська В. М. Вчитель математики Стовпецького ліцею Бажаю успіхів!!!