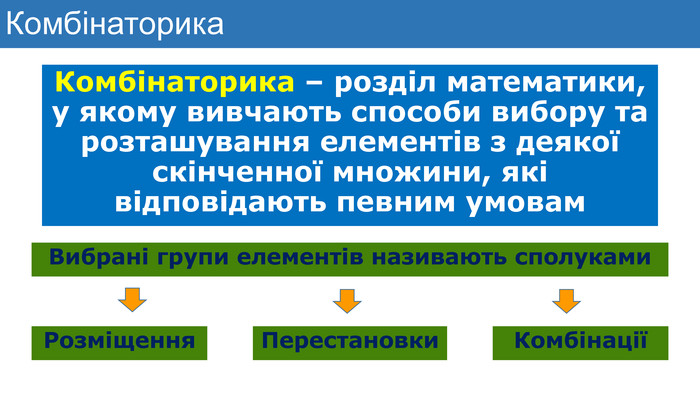
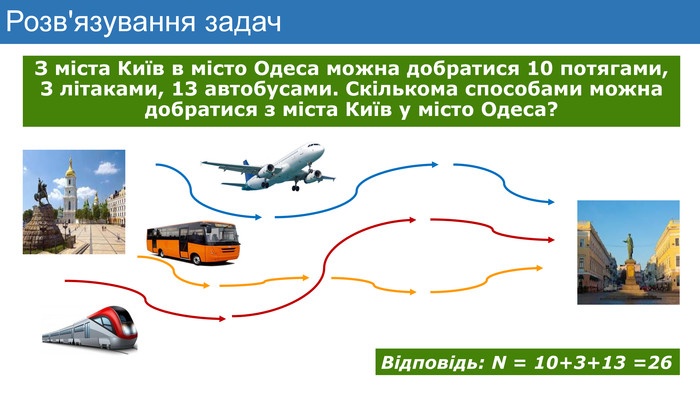
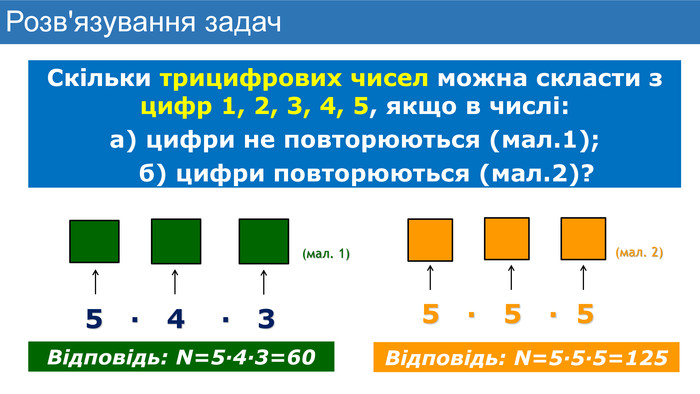
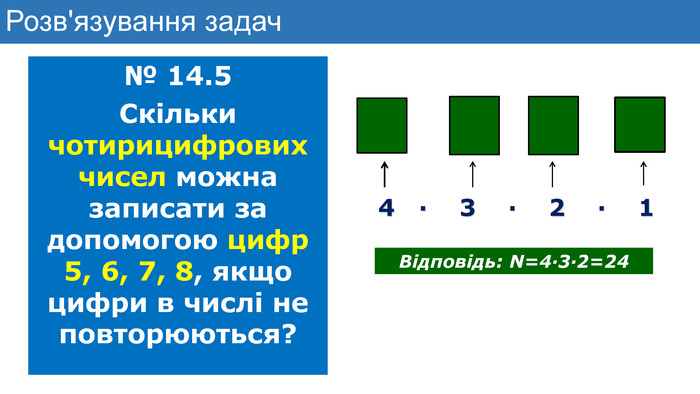
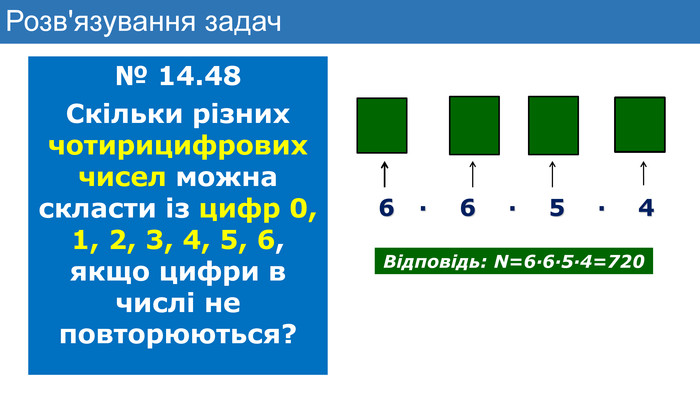
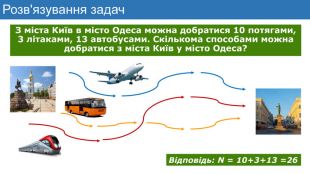
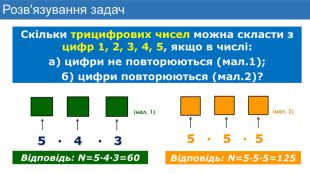
Презентація до уроку математики з теми "Елементи комбінаторики. Правила суми та добутку. Факторіал"
Про матеріал
Презентація до уроку математики з теми "Елементи комбінаторики. Правила суми та добутку. Факторіал" (за підручником Математика. Алгебра та початки аналізу та геометрія. 11 клас. О.Істер. Київ "Генеза" 2019) Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку