Презентація до уроку "Розв’язування квадратних нерівностей". Алгебра 9 клас
Про матеріал
Презентація до уроку "Розв’язування квадратних нерівностей". Алгебра 9 клас за навчальною програмою для загальноосвітніх навчальних закладів з математики для 5-9 класів, затверджена Наказом Міністерства освіти і науки України від 07.06.2017 № 804 Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку










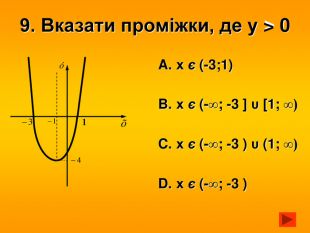
![9. Вказати проміжки, де у > 0х є (-3;1)х є (-∞; -3 ] υ [1; ∞)х є (-∞; -3 ) υ (1; ∞)х є (-∞; -3 ) stroke.colorstroke.onstroke.colorstroke.on 9. Вказати проміжки, де у > 0х є (-3;1)х є (-∞; -3 ] υ [1; ∞)х є (-∞; -3 ) υ (1; ∞)х є (-∞; -3 ) stroke.colorstroke.onstroke.colorstroke.on](/uploads/files/140075/126375/137896_images/10.jpg)
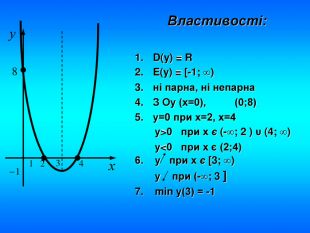
![Властивості: D(y) = RE(y) = [-1; ∞)ні парна, ні непарна. З Оу (х=0), (0;8)у=0 при х=2, х=4 у>0 при х є (-∞; 2 ) υ (4; ∞) у<0 при х є (2;4)6. у при х є [3; ∞) у при (-∞; 3 ]7. min у(3) = -1 fillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.onstroke.colorstroke.onstroke.colorstroke.onstroke.colorstroke.onstroke.colorstroke.on Властивості: D(y) = RE(y) = [-1; ∞)ні парна, ні непарна. З Оу (х=0), (0;8)у=0 при х=2, х=4 у>0 при х є (-∞; 2 ) υ (4; ∞) у<0 при х є (2;4)6. у при х є [3; ∞) у при (-∞; 3 ]7. min у(3) = -1 fillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.onstroke.colorstroke.onstroke.colorstroke.onstroke.colorstroke.onstroke.colorstroke.on](/uploads/files/140075/126375/137896_images/11.jpg)