«ЧИСЛОВІ НЕРІВНОСТІ. ОСНОВНІ ВЛАСТИВОСТІ ЧИСЛОВИХ НЕРІВНОСТЕЙ»
УРОК № 1
ТЕМА: «ЧИСЛОВІ НЕРІВНОСТІ. ОСНОВНІ ВЛАСТИВОСТІ ЧИСЛОВИХ НЕРІВНОСТЕЙ» (слайд 1)
Мета уроку: (слайд 2)
сформувати поняття числової нерівності і основних властивостей числових нерівностей та їх наслідків;
домогтися засвоєння учнями змісту означення і властивостей числових нерівностей, свідомо використовувати при розв’язанні вправ різного рівня;
виховувати інтерес до вивчення матеріалу.
Тип уроку: засвоєння знань, вироблення вмінь
Обладнання: картки настрою, підручник, комп’ютер, проектор.
Хід уроку
І. Організаційний етап.
Вступна бесіда вчителя по курсу 9 класу: вчитель називає теми, з якими учні ознайомляться на протязі року, наголошуючи на необхідності підготовки до державної підсумкової атестації, аналізує будову підручника.
ІІ. Формування мети і завдань уроку. Мотивація навчальної діяльності учнів.
Вчитель: Ми досить часто порівнюємо величини на практиці.
Визначте, який із записів зайвий. Відповідь обґрунтуйте. (слайд 3)
18 > 12; 0,49 < 0,5; – 3 > 2; – 4 < 0;
0,7 = 1,3 – 0,6; 17 > – 100.
Висновок: раніше було вивчено питання про види, властивості, способи перетворення виразів, що не містять ділення на змінну, тепер ми будемо вивчати способи претворення виразів.
ІІІ. Актуалізація опорних знань та вмінь учнів. (слайд 4-5)
- Порівняйте числа:
а) 51 і 99; б) ![]() і
і ![]() ; в) 5,367 і 5,371.
; в) 5,367 і 5,371.
-
Порівняйте вирази: а)
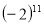 і
і 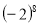 ; б) – 2,114 і
; б) – 2,114 і 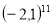 .
.
- Яке з чисел лежить праворуч на числовій осі:
а) – 13 і 2; б) -4 і -7; в) – 0,2 і – 0,7; г) ![]() і
і ![]() .
.
ІV. Формування знань і вмінь.
- Числа можна порівнювати не тільки за допомогою вивчених правил.
Означення. Число а більше від числа в, якщо а – в > 0;
Число а менше числа в, якщо а – в < 0.
Види нерівностей
строгі а < в, а > в
нестрогі а ≤ в, а ≥ в (слайд 6)
Закріплення означення. Порівняти числа, якщо
а – в = - 0,001; а – в = 21,7; а – в = 0 (слайд 7)
Робота за підручником:
усно - № 1, № 2, № 4, № 5, №11, №16, №18;
письмово - №8 ( завдання 1,3,5 – розв’язуємо біля дошки, 2,4,6 - індивідуально), №13.
- Розглянемо основні властивості числових нерівностей. (слайд 8-9)
Теорема 1. Якщо а > в, в > с, то а > с
Дано: а > в, в > с
Довести: а > с
Доведення
Якщо а > в, то а – в > 0; в > с , то в – с > 0
Запишемо суму – сума двох додатних чисел – додатне число:
(а – в) + (в – с ) = а – в + в – с = а – с > 0
Теорема 2. Якщо а > в, с – будь-яке число, то а + с > в + с
Теорема 3. Якщо а > в, с > 0, то ас > вс
Якщо а > в, с < 0, то ас < вс
Наслідок. Якщо ав > 0 і а > в, то ![]() <
< ![]()
Теореми 2 і 3 – самостійно доведення за підручником вдома.
Закріплення основних властивостей.
№ 37 (усно), № 39 (письмово)
- Знайти помилку: (слайд 10)
а) m > n, то m + 3 > n + 3;
б) 5 > 3, 3 > - 7, то 5 < - 7;
в) а > 5, то а +4 > 9;
г) а > 5, то 4а > 20.
V. Підсумок уроку.
Як ми тепер можемо порівняти числа?
Знайдіть і виправте помилки, ураховуючи, що х > у, х > 0, у > 0, z > 0.
- х < у;
- х + а < у + а;
- х + z < у;
- zх > у z;
-
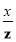 >
> 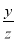 ;
;
-
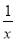 >
>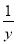 . (слайд 11)
. (слайд 11)
VІ. Домашнє завдання. Виставлення оцінок. (слайд 12)
- §1, §2 вивчити означення порівняння чисел; зміст і доведення числових нерівностей.
- виконати № 3, 19, 36, 38, 40.
VІІ. Рефлексія.
Ваш настрій після уроку? Піднесіть будь-ласка картки (червоний, жовтий, чорний)


про публікацію авторської розробки
Додати розробку
