Урок "Арифметична та геометрична прогресії"

План-конспект уроку

з алгебри

в 9-А класі

Розв’язування задач та вправ із теми «Арифметична та геометрична прогресії»

Вчитель: Колісниченко Г.А.

Березень 2019

Тип уроку: відпрацювання умінь і навичок.

Обладнання. дидактичний матеріал, комп’ютер, комп’ютерна презентація.

ХІД УРОКУ

І. Організаційний момент.

Перевіряю готовність учнів до уроку, налаштовую на роботу.

ІІ. Перевірка домашнього завдання

Перевірка домашнього завдання відбувається вибірково.

ІІІ. Постановка мети і завдань уроку

"Прогресія", "прогрес", "прогресивний" – слова одного кореня.

Прогресія – явище без перебільшення, унікальне. Історія виникнення прогресії сягає глибини віків.

Підсумовуванням арифметичних і геометричних прогресій та складанням відповідних задач займалися багато любителів математики протягом багатьох століть. Найдавнішою задачею на прогресії є задача про розподіл хліба, записана в Єгипетському папірусі Рінда, яка відноситься до III ст. до н. є. Зміст її приблизно такий :"Сто мір хліба слід розділити між п'ятьма людьми так, щоб другий одержав на стільки ж більше від першого, на скільки третій одержав більше від другого, четвертий більше - більше від третього і п'ятий - більше від четвертого. Крім того, двоє перших повинні одержати в 7 раз менше за трьох інших. Скільки потрібно дати кожному?"

Перші задачі на прогресії пов'язані із запитами господарського життя і суспільної практики (розподіл спадщини, одержання винагороди), із спостережень над явищами природи, з досліджень суспільно-економічних явищ.

Зміст ряду історичних задач на прогресії, відображає той подив, який виникав в тих, хто розв'язував ці задачі.

Ми сьогодні з вами на уроці просто, чітко і з легкістю узагальнимо знання з теми: «Арифметична та геометрична прогресія», закріпимо навички обчислення елементів прогресії, покажемо практичне застосування теми на прикладах задач із різних сфер життя та навколишнього життя. Тому я очікую злагодженої роботи, взаємодопомоги, взаємоповаги, гарних результатів.

IIІ. Перевірка домашнього завдання

Під час перевірки домашнього завдання запитую чи виникли труднощі. Запитую правильні відповіді домашнього завдання вибірково в учнів.

IV. Актуалізація опорних знань учнів

Вправа «Закінчи речення»

1) Арифметичною прогресією називають послідовність, кожний членякої, починаючи з другого, ...

2) Для арифметичної прогресії з першим членом а₁та різницею d її n-й член можна знайти за формулою …

3) Сума перших n членів арифметичної прогресії дорівнює …

4) Геометричною прогресією називають послідовність, кожний член якої, починаючи з другого, ...

5) n-й член геометричної прогресії дорівнює добутку його першого членана ...

6) Сума членів скінченної арифметичної прогресії дорівнює...

Вправа

1) Чи є послідовність арифметичною прогресією, якщо так то назвіть різницю:

1.     1; 5; 9; 13.
2.     25; 22; 19; 16.
3.     2; 7; 11; 14
4.     5; 25; 45; 65
5.     -7; 0; -7; 0.

2) Чи є послідовність геометричною прогресією, якщо так то назвіть знаменник:

1.     8; 8; 8; 8.
2.     10; 20; 30; 50.
3.     3; 9; 27; 81
4.     5; 0; 0; 0
5.     -7; 7; -7; 7.

V. Розв'язування задач прикладного змісту

А зараз розглянемо задачі із різних сфер діяльності людини на прогресії.

ПРОГРЕСІЯ В ПРИРОДІ

Найкращим прикладом прогресій слугує природа. Вчені-біологи виявили, що одноклітинні мікроорганізми розмножуються з геометричною прогресією.

Інтенсивність розмноження бактерій використовують у харчовій промисловості (для приготування напоїв, кисломолочних продуктів, при квашенні, солінні і ін.), у фармацевтичній промисловості (для створення ліків, вакцин), в сільському господарстві (для приготування силосу, корму для тварин та ін.), в комунальному господарстві та природоохоронних заходах (для очищення стічних вод, ліквідації нафтових плям).

Задача 1.

Кожна найпростіша одноклітинна тварина інфузорія-туфелька розмножується поділом на 2 частини. Скільки інфузорій було спочатку, якщо після шестиразового поділу їх стало 320?

Розв’язання:

Нехай спочатку було b₁ інфузорій. Кількість інфузорій збільшується з геометрично прогресією. Тоді після шостого поділу їх слало

інфузорій

Відповідь: 5 інфузорій  було спочатку.

Ці ж закони діють і для розмноження рептилій, птахів, ссавців. Використовуючи загальновідомі формули і спеціальні знання, вчені-природознавці можуть розрахувати приріст тварин в заповідниках і в дикій природі.

Задача 2.

У зв'язку з надмірним полюванням на лисиць в Англії різко зросло поголів'я кроликів, які з'їдали посіви фермерів. Як швидко росла їх кількість, якщо в одному з округів Англії їх було штук, а за шість років стало ?

Розв’язання: ,  , . . Підставивши відомі величини у формулу, матимемо: , .

Відповідь: За кожен рік кількість кролів зростала в середньому на .

Задача 3.

При вільному падінні тіло проходить за першу секунду 4,9 м, а за кожну наступну на 9,8 м більше. Знайдіть глибину шахти, якщо камінець досяг її дна через 8 с після початку падіння.

Розв'язання:

Маємо арифметичну прогресію, у якої .

.

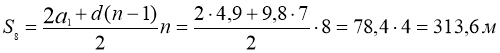Відповідь: 313,6 м.

ПРОГРЕСІЇ В БУДІВНИЦТВІ І ІНЖЕНЕРНІЙ СПРАВІ

Інколи формулами арифметичної прогресії користуються в своїх розрахунках інженери. Наприклад, при будівництві будівель і конструкцій.

Задача 4.

Артур вирішив зробити садову драбину з таким розрахунком, щоб нижній щабель мав довжину 50 см, а кожен із наступних 12 щаблів були на 2 см коротші попереднього. Якої довжини повинен бути верхній щабель драбини?

Дано:

Найти:

Розв’язання:

Відповідь: 26 см.

ПРОГРЕСІЇ В МЕДИЦИНІ І ПЛАНУВАННЯ ЛІКУВАННЯ

Задача 5.

Курс повітряних ванн починають з 15 хв. в перший день і збільшують час цієї процедури кожного наступного дня на 10 хвилин. Скільки днів слід приймати ванни в зазначеному режимі, щоб досягти їх максимальної тривалості 1 годину 45 хвилин?

Дано:

а₁= 15 хв

d = 10

a_n = 1год 45 хв = 105 хв

Найти:

n = ?

Розв’язання:

a_n = a₁+ d · (n - 1)

105 = 15 + (n – 1) · 10

105 = 15 +10 n – 10

-10n = 15 – 10 – 105

-10n = -100

n = 10

Відповідь: 10 днів.

(Додаткова задача )

Хворий приймає ліки за наступною схемою: перший день – 5 крапель, а кожного наступного дня – на 5 крапель більше. Дійшовши до сорока крапель він три дні приймає таку саму дозу (по 40 крапель), а потім щодня зменшує дозу на 5 крапель, поки не дійде до 5-ти крапель за день. Скільки пляшечок ліків треба купити хворому, якщо кожна пляшечка вміщує 20 мл ліків (що становить 250 крапель)?

Розв’язання

Знайдемо кількість днів поки кількість крапель стане 40.

Знайдемо кількість крапель за 8 днів: . На 9-й день – 40 капель і ще 180 до зменшення до 5 крапель.

Всього крапель. Отже для лікування потрібно 2 пляшечки крапель.

Відповідь: 2 пляшечки.

ПРОГРЕСІЇ В СПОРТІ

Задача 6.

Альпіністи в перший день сходження піднялися на висоту 1400 м, а потім кожен наступний день вони долали на 100 м менше, ніж за попередній. За скільки днів вони підкорили висоту в 5000 м?

Дано:

Розв’язання:

- не задовольняє умові задачі.

Відповідь: за 4 дні.

ПРОГРЕСІЇ І ФІНАНСИ

Задача 7. (ЗНО-2010)

Одним із мобільних операторів було запроваджено акцію «Довше розмовляєш – менше платиш» з такими умовами: плата за з’єднання відсутня; за 1 хвилину розмови абонент сплачує 30 копійок, а за кожну наступну хвилину розмови – на 3 копійки менше, ніж на попередню; плата за одинадцяту та всі наступні хвилини не нараховується; умови дійсні для дзвінків абонентам усіх мобільних операторів країни. Скільки за умовами акції коштуватиме абоненту цього мобільного оператора розмова тривалістю 8 хвилин (у гривнях)?

Розв'язання:

Маємо арифметичну прогресію, у якої .

.

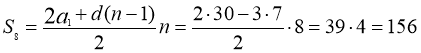Відповідь: 1,56 грн.

Задача 8.

Уявіть, що вам деяка фірма пропонує свої послуги. Щодня ви можете брати у фірми по 100 грн. Але за перший день ви зобов'язані заплатити фірмі 1к, за другий - 2к, за третій - 4к. і т. д. Чи укладете ви з цією фірмою договір не менш ніж на 20 днів за таких умов?

Розв'язання:

Від фірми отримуємо - 2000 грн, а повинні будемо заплатити за це суму, що дорівнює S₂₀ для геометричної прогресії, де . Тобто:

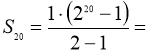1 048 576 – 1 = 1 048 575(коп.)=10485грн. 75к

Ви маєте бути компетентними у фінансових питаннях, і тому освіченість особистості, як ніколи, на першому місці.

VІ. Підведення підсумків.

Вправа «Знайди помилку»

VII. Домашнє завдання

Проводиться оцінювання учнів.

За допомогою мережі Інтернет знайти 3 прикладні задачі на прогресії та розв’язати їх.