Презентація до уроку "Розв'язування прямокутних трикутників"

Урок геометрії 8 клас Кинашівська ЗОШ І-ІІІ ступенів

Життя сьогодні ставить підвищені вимоги до практичної підготовки працівників різних галузей народного господарства ще за шкільною партою. Серед напрямів, що можуть поліпшити рівень загальноосвітньої математичної освіти, є посилення практичного та прикладного спрямування шкільного курсу математики, забезпечення реального зв’язку навчання з життям. Під практичною спрямованістю розуміють навчання безпосередньому застосуванню знань, які отримали учні під час вивчення теоретичного курсу математики. Прикладна ж спрямованість передбачає вироблення в учнів умінь використовувати здобуті під час вивчення математики знання в своїй практичній діяльності. Без практичного спрямування будь-якої теми з математики не може бути успішного її засвоєння учнями. У зв’язку з цим проблема прикладного та практичного спрямування навчання учнів математики була і запишається завжди актуальною.

Мета: закріпити, систематизувати і перевірити знання з даної теми; повторити означення синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника, теорему Піфагора та основні наслідки з неї; закріпити вміння і навички застосувати теоретичний матеріал до розв'язування прямокутних трикутників; показати практично-прикладний характер здобутих знань. Розвивати міжпредметні зв'язки, вміння аналізувати, робити висновки, знаходити власні способи розв’язання. Формувати компетентності: соціальні (розвиток пізнавальної активності учнів, робота в команді, усвідомлення власного внеску в спільну роботу, вміння брати відповідальність), комунікативні (формування власної точки зору, розвиток культури мовлення, вміння доводити власну позицію). Виховувати активність, увагу, кмітливість, самостійність, пізнавальний інтерес до вивчення математики. Тип уроку: урок застосування знань, умінь і навичок. Форма проведення: урок - мандрівка Обладнання: картки із завданнями, задачі – малюнки, таблиці Брадіса, калькулятори, таблиці-вислови, комп’ютер, презентація, портрети вчених, практичні задачі в малюнках.

«Серед рівних розумом – за однакових інших умов – переважає той, хто знає геометрію». Блез Паскаль

А В С Означення : Прямокутним називається трикутник у якого один кут прямий. катети гіпотенуза

А В С Властивості прямокутного трикутника 1. Сума гострих кутів прямокутного трикутника дорівнює 90є. А+ В 2. Катет , який лежить проти кута 30є дорівнює половині гіпотенузи . Якщо А = 30є , то ВС = 0,5АВ

А В С Теорема Піфагора У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів . АВІ =АСІ+ВСІ

А В С Означення Синусом гострого кута прямокутного трикутника називається відношення протилежного катета до гіпотенузи . sinА = ВС АВ sinВ = АС АВ

А В С Означення Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи . cosА = АС АВ cosВ = ВС АВ

А В С Означення Тангенсом гострого кута прямокутного трикутника називається відношення протилежного катета до прилеглого . tgА = ВС АС tgB = АС ВС

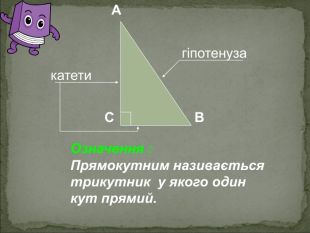
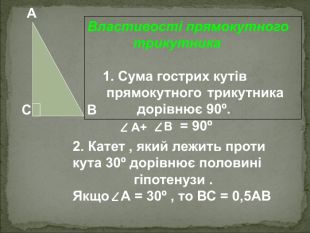
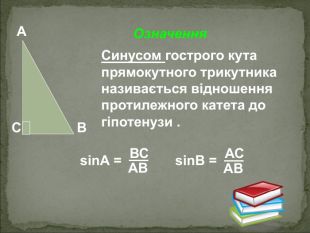
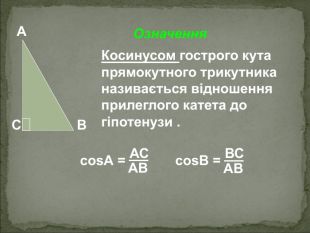
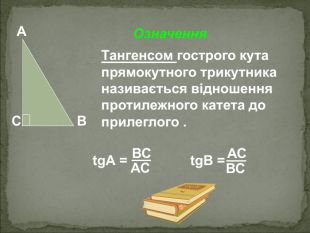
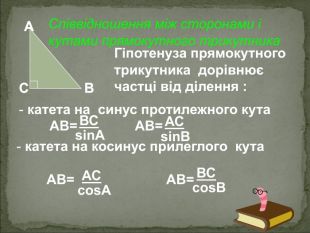
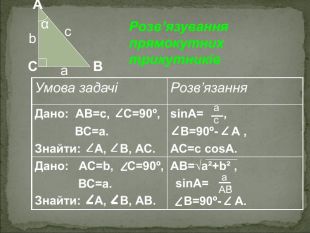
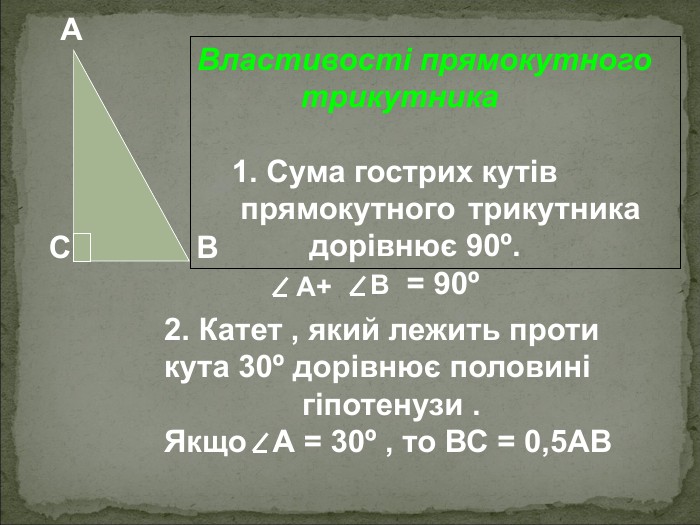
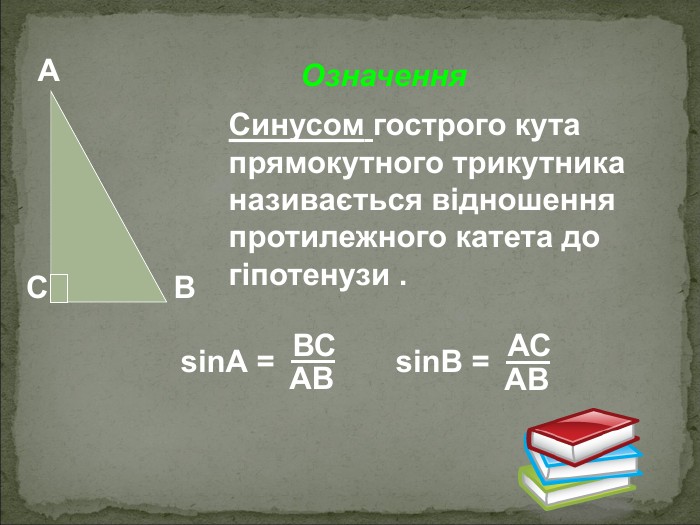
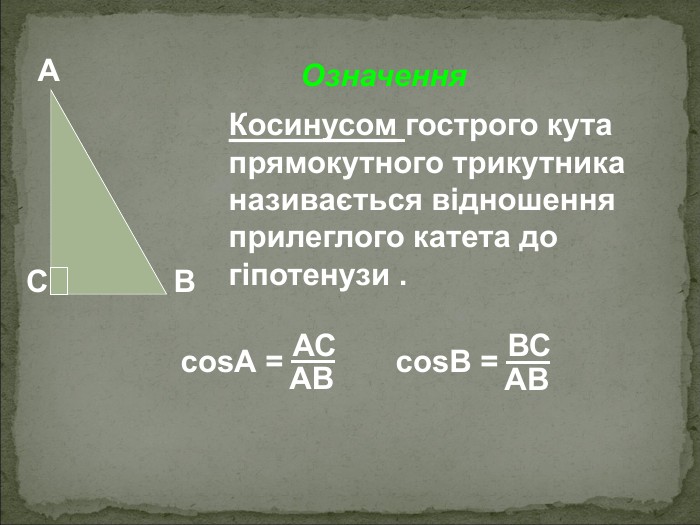
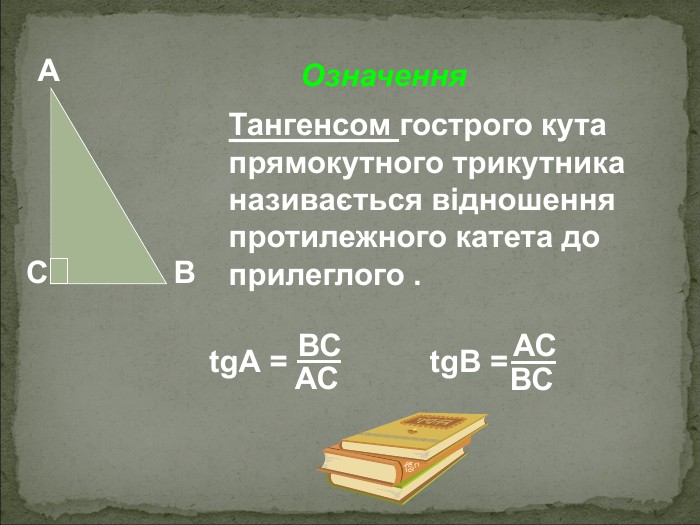
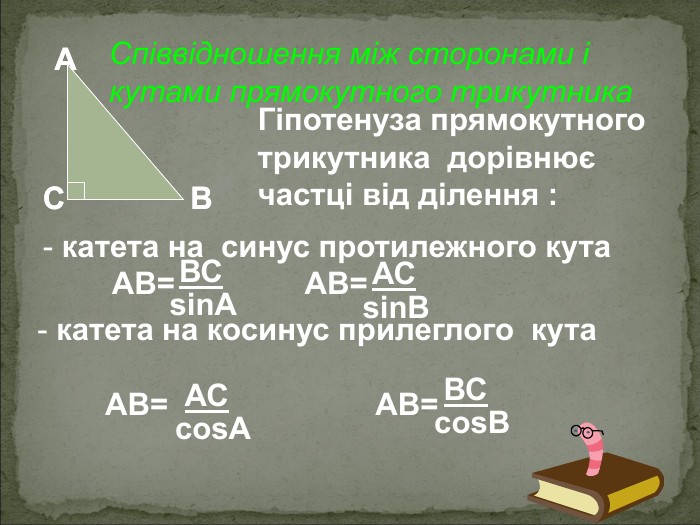
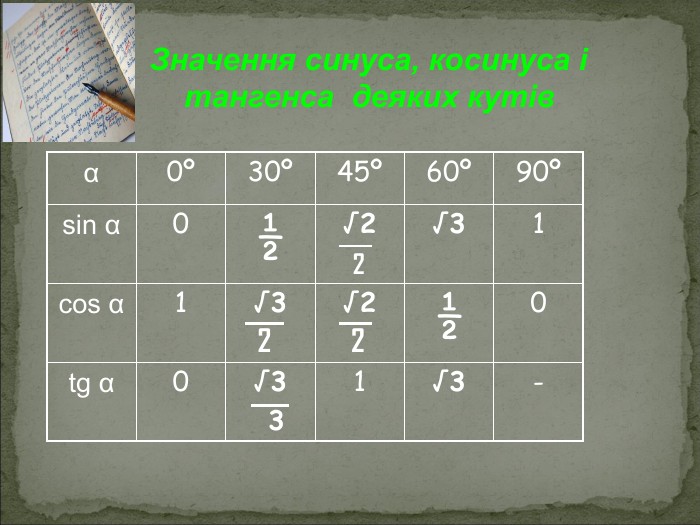
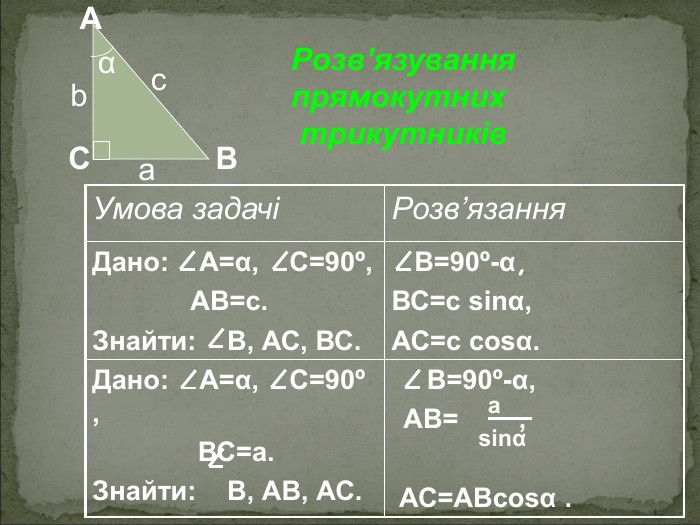
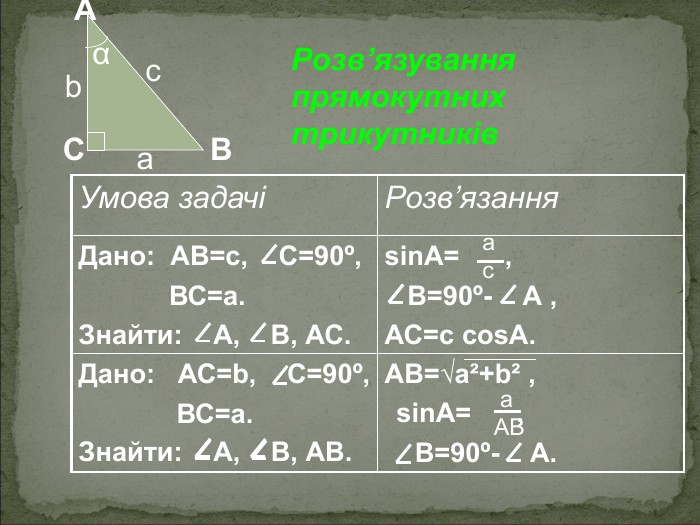
А В С Співвідношення між сторонами і кутами прямокутного трикутника Катет прямокутного трикутника дорівнює добутку: гіпотенузи на синус протилежного кута АС=АВsinB BC=ABsinA гіпотенузи на косинус прилеглого кута AC=ABcosA ВC=ABcosВ - другого катета на тангенс протилежного кута AC=BCtgB BC=ACtgA

А В С Співвідношення між сторонами і кутами прямокутного трикутника Гіпотенуза прямокутного трикутника дорівнює частці від ділення : катета на синус протилежного кута АВ= АB= катета на косинус прилеглого кута AВ= АВ= ВС sinA АС sinВ АС cosA ВС cosВ А В С

Значення синуса, косинуса і тангенса деяких кутів α sin α 0 √2 √3 1 cos α 1 √3 √2 0 tg α 0 √3 3 1 √3 - 2 2 2

Перевір себе Який трикутник називається прямокутним? Сформулюйте теорему Піфагора. Сформулюйте властивості прямокутного трикутника. 4 Що називається синусом гострого кута прямокутного трикутника? 5 Як знайти катети за гіпотенузою і гострим кутом? 6 Як знайти гіпотенузу за катетами ?

Піфагор Самоський (580-500рр до н.е ) Давньогрецький філософ, вчений , математик. Зробив значний вклад в розвиток тогочасної науки. Відкрите ним правило знаходження величин сторін прямокутного трикут- ника, назване нині “теоремою Піфагора”, є головною і найкращою теоремою геометрії.

Розв’язування прямокутних трикутників Умова задачі Розв’язання Дано: А=α, С=90є, АВ=с. Знайти: В, АС, ВС. В=90є-α, ВС=с sinα, АС=с cosα. Дано: А=α, С=90є , ВС=а. Знайти: В, АВ, АС. В=90є-α, АВ= , АС=АВcosα . а sinα А В С α с b а

Умова задачі Розв’язання Дано: АВ=с, С=90є, ВС=а. Знайти: А, В, АС. sinА= , В=90є- А , АС=с cosА. Дано: АС=b, С=90є, ВС=а. Знайти: А, В, АВ. АВ=√аІ+bІ , sinА= , В=90є- А. Розв’язування прямокутних трикутників а с а АВ а А В С α с b

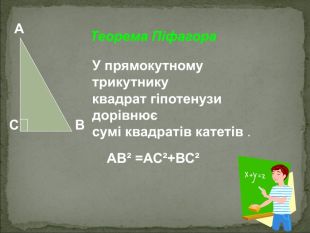
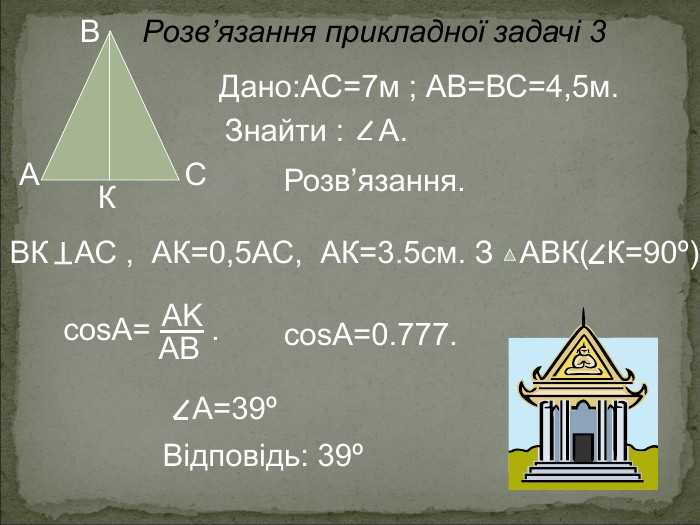
Задача 1. Як далеко видно з повітряної кулі, що піднялася на висоту 4 км над Землею (радіус Землі приблизно дорівнює 6370 км).  Розв'язання. 1. За теоремою про властивість дотичної до кола, дотична перпендикулярна радіусу, проведеному в точку дотику, тобто   OTM  = 90 о. . 2. MO = 6370 +4 = 6374 км. 3. За теоремою Піфагора:  MT 2 + OT 2 = MO 2  MT 2 = MO 2 - OT 2  MT = 112,9 км 

Задача 2. Знайти довжину драбини, прикладеної до будинку, якщо один її кінець знаходиться на відстані 4м від будинку, а другий на зіткненні стіни і даху. Висота будинку дорівнює 8м. Задача 3. Ширина фронтона 7 м, довжина крокви 4,5 м. Під яким кутом крокви нахилені до стелі ?

Розв’язання. А В С Дано:АС=7м ; АВ=ВС=4,5м. Знайти : А. К ВК АС , АК=0,5АС, АК=3.5см. З АВК( К=90є) Τ Розв’язання прикладної задачі 3 cosA= . AK AB cosA=0.777. А=39є Відповідь: 39є

Задача 4. Знайдіть кут підйому дороги від мосту до пам'ятника, якщо на відстані 200 м висота підйому становить 8 м.

Задача 5. На березі річки тополя росла та вітру порив її стовбур зламав. Тополя упала і стовбур її кут прямий з течією річки утворив. Памятайте у тому місці ріка 4 фути була шириною. Верхівка схилилась до краю, залишивши 3 фути всього під водою. Скажіть, тополя якої була висоти ?(1фут = 0,3м.) Задача 6. Знайти ширину водоймища між деревами, одне з яких знаходиться на відстані 20 м від нашого місцезнаходження на мосту і відхилене на захід на 32 °, а друге — відхилене на схід на кут 28 ° і знаходиться на відстані 50 м від нас.

Задача 7. Над озером тихим Висотою з півфута підіймалась лотоса квітка, яка росла одиноко. Та вітер скаженим поривом відніс її в бік. І не стало видно квітки над водою. Знайшов же її тільки рибалка ранньою весною в двох футах від місця, де вона росла. Яка в цьому місці на озері води глибина? Розв’язання. Нехай CD = х футів, тоді відстань від лотоса до точки B - (х+0,5)футів. Ця відстань дорівнює гіпотенузі прямокутного трикутника BCD. За теоремою Піфагора маємо: ВD2=DС2+ВС2,отже: (х + 0,5)2 = 22 + х2; х2 + х + 0,25=4 + х2, х = 3,75. Відповідь: 3,75 фути.

1 2 3 4 5 6 7 1. Назва прямокутного трикутника зі сторонами 3, 4, 5. 2. Учений, ім’ям якого названа теорема про суму квадратів катетів прямокутного трикутника. 3. Острів, на якому народився цей учений. 4. Катет, який не лежить проти даного кута. 5. Там Піфагор прожив 12 років. 6. Сторона прямокутного трикутника, яка лежить проти прямого кута. 7. Кількість биків, принесена Піфагором у жертву богам після доведення теореми.

Вчення Піфагора Нічому не дивуйся Тимчасова невдача краща від тимчасової удачі Не заплющуй очі, коли хочеш спати, не проаналізувавши своїх учинків за минулий день Твори велике, не обіцяючи великого Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями Не роби нічого ганебного ні в присутності інших, ні таємно. Першим твоїм законом повинна бути повага до самого себе Лише неблагородна людина здатна в очі хвалити, а поза очі злословити Усе в світі підкоряється числам

Домашнє завдання Задача. Вершину дерева, віддаленого від даного пункту на 16 м, видно під кутом 16є до горизонту , а вершину другого дерева віддаленого від цього самого пункту на 24 м, видно під кутом 19є. Яке дерево вище і на скільки?