многокутник

геометрична фігура, замкнена ламана (сама, або разом із точками, що лежать усередині). Вершини цієї ламаної називають вершинами многокутника, а відрізки ламаної — сторонами многокутника.

Дві вершини, що сполучаються відрізком ламаної, називаються суміжними вершинами. Дві сторони, що мають спільну вершину, називаються суміжними. Якщо дві несуміжні сторони не мають спільних точок (тобто ламана, що обмежує многокутник, не перетинається), многокутник називається простим

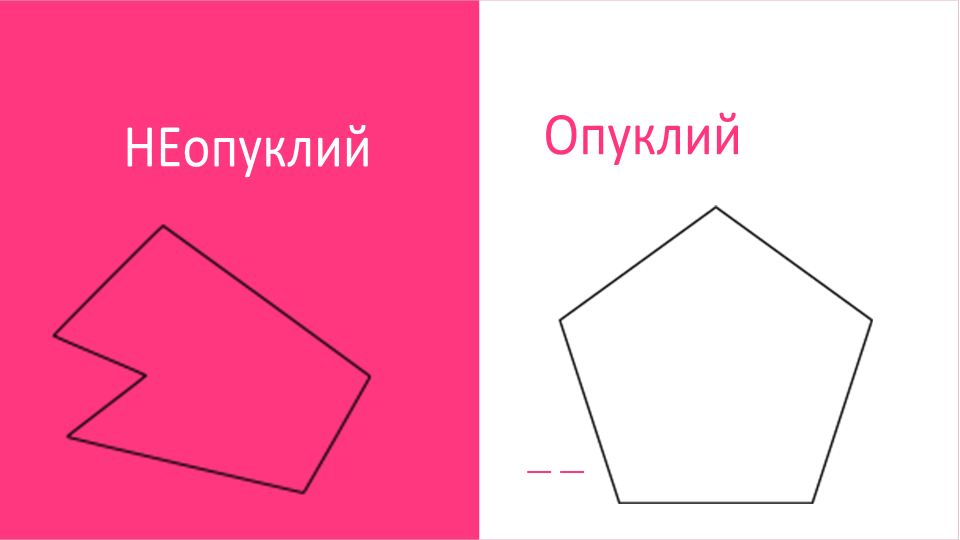
Опуклий многокутник

●        многокутник буде опуклим, якщо відносно будьякої прямої, що проходить через сторону многокутника, многокутник повністю буде розташований у півплощині, утвореній цією прямою (тобто по один бік від прямої).

●        многокутник без самоперетинів такий, що кожний внутрішній кут не перевищує 180°;

●        многокутник такий, що всі його діагоналі повністю лежать всередині нього;

●        многокутник є опукла оболонка кінцевого числа точок на площині;

●        многокутник є перетином кінцевого числа замкнутих півплощин.

НЕопуклий многокутник

●         Деякі прямі, що містять внутрішні точки увігнутого багатокутника, перетинають його межу більш ніж у двох точках.Деякі діагоналі увігнутого багатокутника лежать частково або повністю поза ним.^] Деякі бічні прямі, проведені через сторону увігнутого багатокутника не можуть розділити площину на дві півплощини так, щоб многокутник повністю належав одній з них. Жодне з цих трьох тверджень не виконується для опуклого багатокутника.

●         Як і для будь-якого простого багатокутника, сума внутрішніх кутів увігнутого багатокутника становить π (n  

—   2) радіан, або 180 ° × (n   —   2), де n — кількість сторін.

●         Завжди можна розділити увігнутий многокутник на множину опуклих многокутників. Алгоритм, який виконує декомпозицію на якомога меншу кількість опуклих багатокутників за поліноміальний час описується Chazelle та Dobkin, (1985).

●         Трикутник ніколи не може бути увігнутим, але існують увігнуті полігони з n сторін для будь-якого n > 3.

Прикладом увігнутого чотирикутника є дельтоїд.

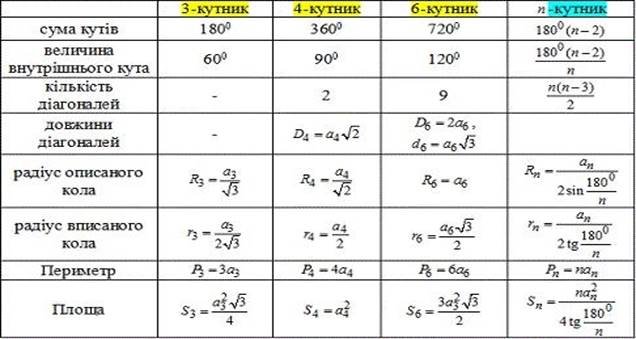
Формули многокутника