Презентація до уроку Розв’язування задач з теми Теорема Піфагора
Про матеріал
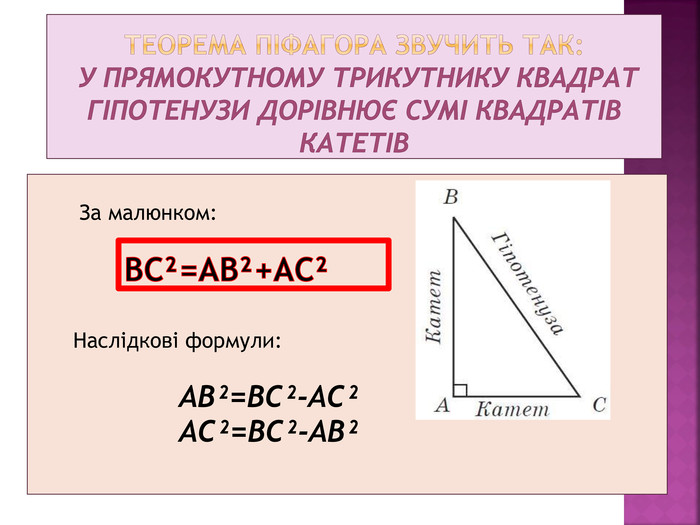
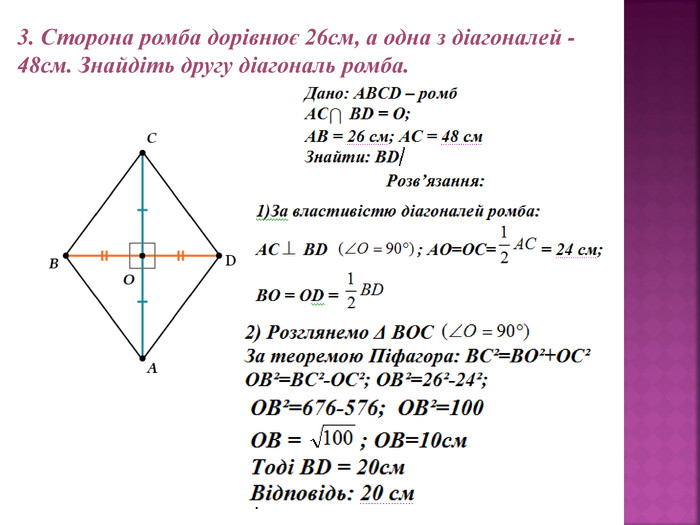
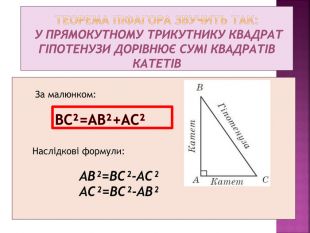
Презентація до уроку: Розв’язування задач з теми Теорема Піфагора. У презентації подано теоретичні відомості з даної теми та наведені задачі з покроковим поясненням. Зручно використовувати даний матеріал під час дистанційного навчання Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку