Тема: Поняття площі многокутника. Площа прямокутника
8 клас геометрія Батаєва Юлія Петрівна
Тема: Поняття площі многокутника. Площа прямокутника
Мета:
- навчальна: закріпити та систематизувати знання учнів про:
- зміст поняття площі многокутника та його властивості;
- формули для обчислення площ прямокутника та паралелограма, їх наслідки.
Відпрацювати навички застосування набутих знань.
- розвивальна: розвивати логічне мислення, уяву, старанність;
- виховна: виховувати дисципліну, повагу до людей та до себе.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
- Організаційний момент
- Актуалізація опорних знань та вмінь
Засвоєння змісту теоретичного матеріалу та його розуміння перевіряється під час виконання учнями математичного диктанту.
Математичний диктант
|
|
Варіант 1 |
Варіант 2 |
|
1 |
Яка площа однієї з двох рівних фігур, якщо площа іншої дорівнює 15 см2? |
Фігуру розбито на 2 частини, площі яких відповідно дорівнюють 15 і 5 м2. Яка площа цієї фігури? |
|
2 |
Обчисліть площу прямокутника зі сторонами 15 і 5 м |
Обчисліть площу прямокутника зі стороною 7 м |
|
3 |
Обчисліть площу паралелограма, якщо одна з його сторін дорівнює 8 см, а проведена до неї висота 6 см |
Обчисліть площу паралелограма, якщо одна з його сторін дорівнює 7 дм, а проведена до неї висота 6 дм |
|
4 |
Площа паралелограма дорівнює 18дм2, а одна зі сторін 3 дм. Знайдіть висоту, проведену до цієї сторони |
Площа паралелограма дорівнює 18 м2, а одна зі сторін 6 м. Знайдіть висоту, проведену до цієї сторони |
- Застосування вмінь
Повторення параграфу п.23 ст.161 - 163
Задача 1. Знайдіть площу многокутника, зображеного на малюнку 227, якщо сторона клітинки дорівнює 1 см.
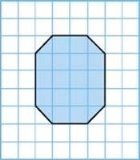
Мал. 227
Р о з в’ я з а н н я. Внутрішня область многокутника складається з шістнадцяти клітинок зі стороною завдовжки 1 см, площа кожної з яких - 1 см2, і чотирьох трикутників, площа кожного з яких дорівнює половині площі клітинки. Отже, площа фігури
S = 16 ∙ 1 + ![]() ∙ 1 ∙ 4 = 18 (см2).
∙ 1 ∙ 4 = 18 (см2).
В і д п о в і д ь. 18 см2.
Розв'язування задач
Задача 1. Знайдіть площу прямокутника ABCD, якщо:
а) АВ = 9 см, ВС = 4 см;
б) AD = 12 см, АС = 13см.
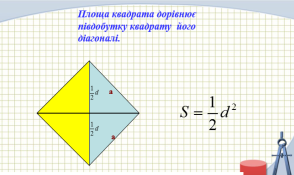
Задача 2. Діагональ квадрата дорівнює ![]() м. Знайдіть площу квадрата.
м. Знайдіть площу квадрата.
Задача 3. Площа прямокутника дорівнює 128 см2. Знайдіть сторони прямокутника, якщо одна з них удвічі більша за іншу.
Задача 4. Бісектриса кута прямокутника ділить його сторону на відрізки завдовжки 3 см і 4 см. Знайдіть площу прямокутника. Скільки розв'язків має задача?
Робота в малих групах
Даний метод інтерактивного навчання передбачає об҆єднання учнів у невеликі групи змішаного типу (слабкі, середні та сильні учні), для спільного виконання задачі.

![]()


![]()
![]()
Задача царівни Дідони
Легенда розповідає, що фінікійська царівна Дідона, рятуючись від своїх ворогів, залишила рідне місто і в супроводі невеликого загону воїнів подалася у пошуках щастя на кораблі вздовж берегів Середземного моря. Обравши зручне місце на південному узбережжі Африки (нинішня Туніська затока), вона вирішила заснувати тут місто і звернулася до вождя місцевого племені з проханням дати їй ділянку землі, яку можна охопити «шкурою бика». Той відразу погодився.
Як Дідоні охопити найбільшу площу для заснування міста? Дідона повелася дуже хитро. Вона наказала розрізати шкуру бика на вузенькі
територію, Дідона заснувала на ній місто Карфаген. Легенда датує цю подію 825 р. до н. е. Очевидно, Дідона розв’язала цікаву математичну задачу, яку часто називають її іменем. Загальне формулювання такої задачі звучить так: «Серед усіх плоских фігур із заданим периметром знайти таку, що має найбільшу площу».
-
Підсумок уроку

ІСТОРИЧНА ДОВІДКА
Дещо про вимірювання площ було відомо геометрам багато тисячоліть тому.
2-3 тисячі років до н. е. вавилоняни вже вміли обчислювати площі прямокутника і трапеції у квадратних одиницях. Еталоном обчислення площ для них був квадрат зі стороною, що дорівнює одиниці довжини. Для обчислення площ прямокутника, трикутника і трапеції давні єгиптяни 4000 років тому використовували ті самі формули, що й ми зараз. У «Началах» Евклід не вживав термін «площа», оскільки під терміном «фігура» мав на увазі частину площини, що обмежена замкненою лінією, тобто площу. Евклід не подавав результат вимірювання площі різних фігур між собою, використовуючи термін «рівновеликі». Так, наприклад, у першій книзі «Начал» можна зустріти задачу 16: «Паралелограми, що знаходяться на різних основах і між тими самими паралельними, рівновеликі. Доведіть!».
Як і інші вчені, Евклід досліджував питання перетворення одних фігур в інші, їм рівновеликі. Так, наприклад, він розв҆язав задачу про побудову квадрата, рівновеликого даному многокутнику.
Повторення засвоєного матеріалу (фронтальне опитування):
- Що таке площа многокутника?
- Як знайти площу многокутника?
- Чи будуть рівними фігури, якщо їх площі рівні?
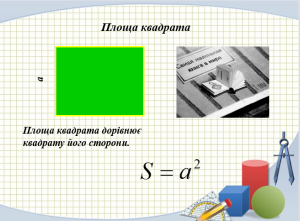
- Як знайти площу прямокутника? Квадрата?
- Домашнє завдання
Повторити п. 23 № 851
Цікаві задачі для учнів неледачих
Задача 1. Скільки дошок потрібно, щоб настелити підлогу в кімнаті довжиною 7,5 м і шириною 5 м, якщо довжина дошки 6 м, а ширина 0,25 м?
Розв’язання: Поверхня підлоги має форму прямокутника, для знаходження площі, потрібно довжину помножити на ширину: S=7.5∙5=37.5(m2). Оскільки дошка теж має форму прямокутника, то її площа : S2=6∙0.25=1.5(m2). Для того, щоб дізнатись, скільки потрібно дошок, треба: k=S:S2 =37.5:1.5=25 (дошок). Відповідь: 25 дошок.
Задача 2. Довести, що із всіх прямокутників з однаковим периметром найбільшу площу має квадрат.
Розв’язання: Нехай квадрат ABCD та прямокутник AKLM, такі, що PABCD=PAKLM.
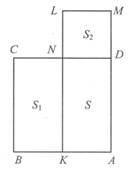
Порівняємо їх площі:
SABCD=S+S1; SAKLM=S+S2.
Порівняємо S1=KN∙KB i S2=DN∙DM.
Але KN>DN i KB=DM, тоді S1>S2.
Отже, SABCD>SAKLM, що й треба було довести.
Задача 3. Яка частина квадрата зафарбована?
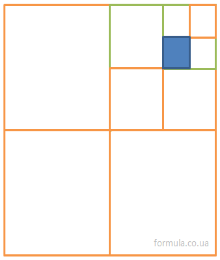
Матеріал для повторення






про публікацію авторської розробки
Додати розробку
