Презентація до уроку ,, Теорема Піфагора''

(Історичний екскурс)

«Геометрія володіє двома скарбами: один з них – це теорема Піфагора» Іоганн Кеплер

Без перебільшення можна сказати, що це сама відома теорема геометрії, бо про неї знає переважна більшість населення планети, хоча довести її здатна лише дуже незначна його частина. Теорема Піфагора!

У чому ж причина такої популярності «піфагорових штанів»? б) простота, а) краса, в) значимість. Знавці стверджують, що причин тут три:

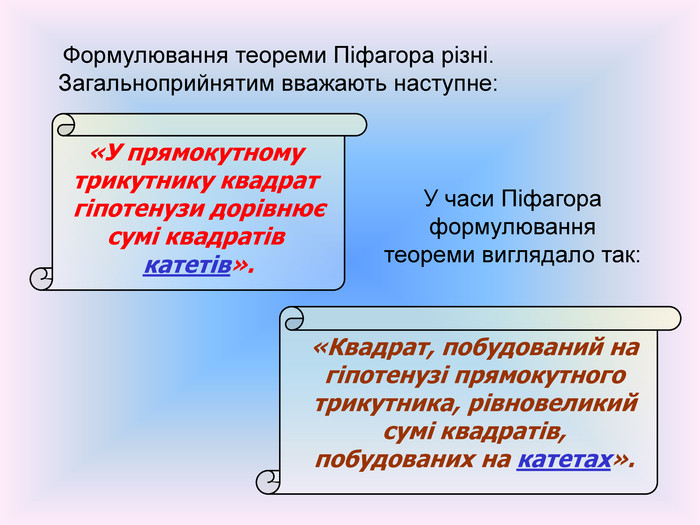
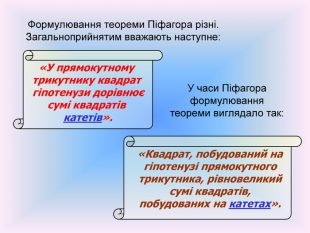
«У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів». Формулювання теореми Піфагора різні. Загальноприйнятим вважають наступне: У часи Піфагора формулювання теореми виглядало так: «Квадрат, побудований на гіпотенузі прямокутного трикутника, рівновеликий сумі квадратів, побудованих на катетах».

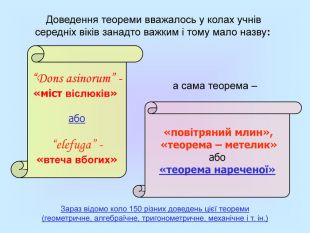
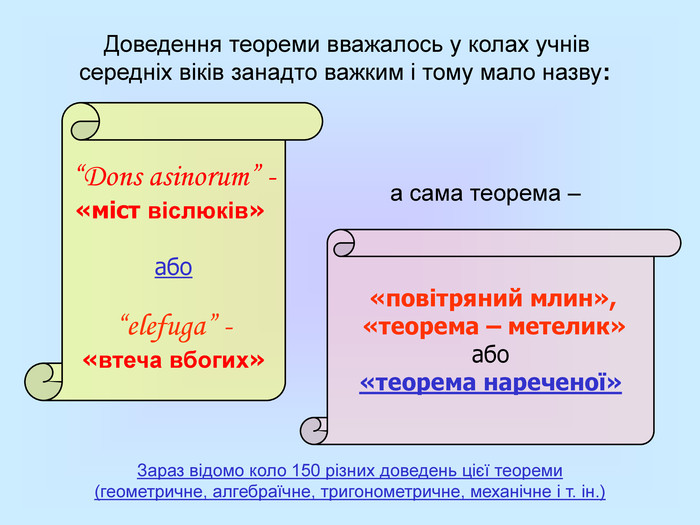
 Доведення теореми вважалось у колах учнів середніх віків занадто важким і тому мало назву: Зараз відомо коло 150 різних доведень цієї теореми (геометричне, алгебраїчне, тригонометричне, механічне і т. ін.) “Dons asinorum” - «міст віслюків» або “elefuga” - «втеча вбогих» «повітряний млин», «теорема – метелик» або «теорема нареченої» а сама теорема –

Доведення, які використовують поняття рівновеликих фігур; Адитивні доведення (основані на розкладі квадратів, побудованих на катетах, на фігури, з яких можна скласти квадрат, побудований на гіпотенузі; Доведення методом добудов; Алгебраїчний метод доведення; Тригонометричний метод доведення; І т. ін.

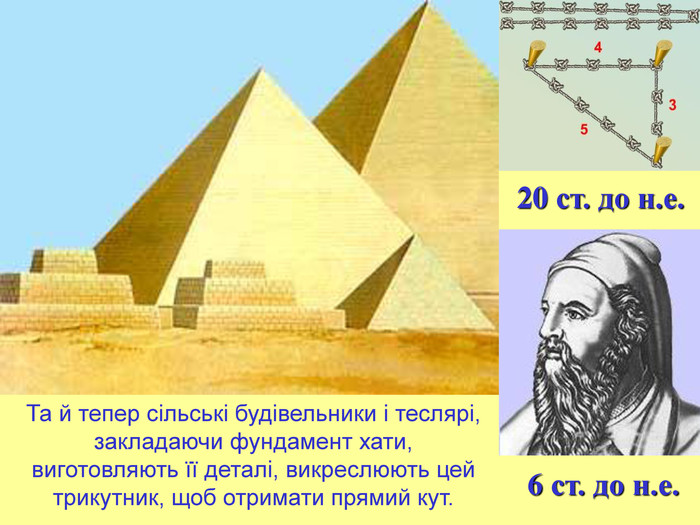
Немає ніякого сумніву, що цю теорему знали за багато років до Піфагора. Так, за 1500 років до Піфагора стародавні єгиптяни знали про те, що трикутник зі сторонами 3, 4 і 5 є прямокутним, і використовували цю властивість (теорему, обернену теоремі Піфагора) для побудови прямих кутів при плануванні земельних ділянок і спорудженні будівель.

20 ст. до н.е. 6 ст. до н.е. Та й тепер сільські будівельники і теслярі, закладаючи фундамент хати, виготовляють її деталі, викреслюють цей трикутник, щоб отримати прямий кут.

Те саме робили тисячі років тому при будові чудових храмів в Єгипті, Вавилоні, Китаї, напевне, і в Мексиці. Як свідчать літописи, у Стародавньому Китаї вже коло 2200 років до н.е. для трикутника зі сторонами 3, 4, 5 було знайдено правило «гоу-гу», за допомогою якого можна було по відомій гіпотенузі і одному з катетів знайти другий невідомий катет, а також гіпотенузу, якщо відомі обидва катети.

У самому давньому індійському геометричному збірнику «Сульвасутра» («Правила мотузки», 600 років до н.е.), який є своєрідною інструкцією по спорудженню олтарів у храмах, даються правила побудови прямих кутів за допомогою мотузки з вузлами, відстань між якими дорівнює 15, 36 і 39 падас (міра довжини). Олтарі за священним писанням повинні мати певну геометричну форму, орієнтовану відносно чотирьох сторін горизонту. 4 3 5

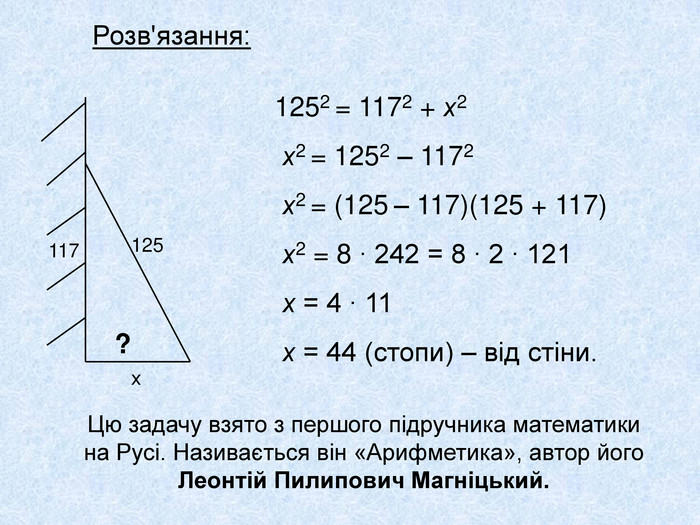
«Палка довжиною 1/2 , притулена до стіни. Її верхній кінець опустили на 1/10 . Як далеко відсунеться її нижній кінець?» У Стародавньому Вавилоні ця властивість не тільки трикутника зі сторонами 3, 4, 5, але і взагалі всіх прямокутних трикутників було добре відомо. Так, в одному із самих ранніх вавилонських математичних текстів міститься наступна витончена задача: ?

В задачі, як бачимо, за даною гіпотенузою c = 1/2 і одному з катетів b = 1/2 – 1/10 = 2/5 необхідно знайти другий катет. Його, як і повинно бути, вавілонянин визначав «за Піфагором»:

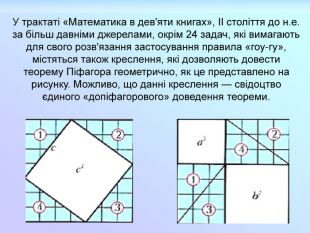
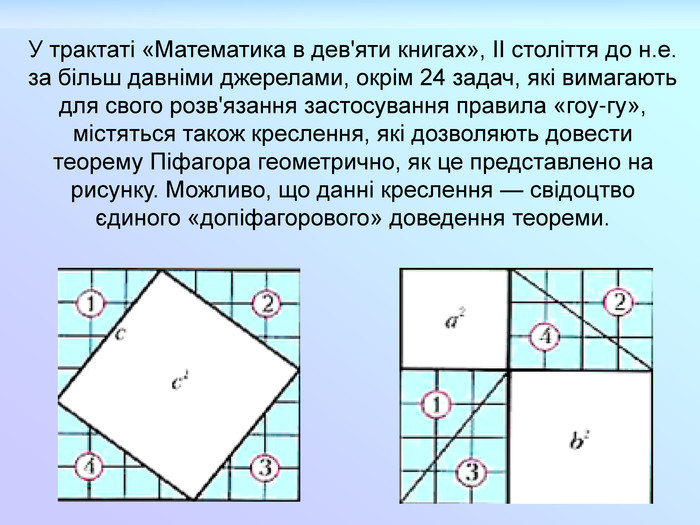
У трактаті «Математика в дев'яти книгах», II століття до н.е. за більш давніми джерелами, окрім 24 задач, які вимагають для свого розв'язання застосування правила «гоу-гу», містяться також креслення, які дозволяють довести теорему Піфагора геометрично, як це представлено на рисунку. Можливо, що данні креслення — свідоцтво єдиного «допіфагорового» доведення теореми.

Евклід. «Початки», 1482 р.

Більша частина доведень теореми Піфагора виконана геометричними методами, серед яких переважне місце займає метод розкладу. Суть метода розкладу в тому, що квадрат, побудований на гіпотенузі, з однієї сторони, і квадрати, побудовані на катетах, з другої, складаються з рівних частин. Найпростіший приклад застосування цього метода маємо при доведенні теореми Піфагора для рівнобедреного прямокутного трикутника (див. рис.). З цього рисунка все так зрозуміло, що коментувати його не потрібно. Як писав у подібних випадках індійський математик XII століття Бхаскара: «Дивись!»

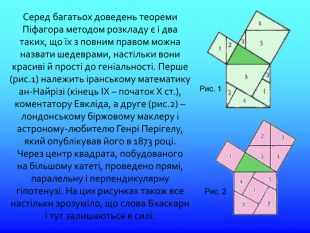
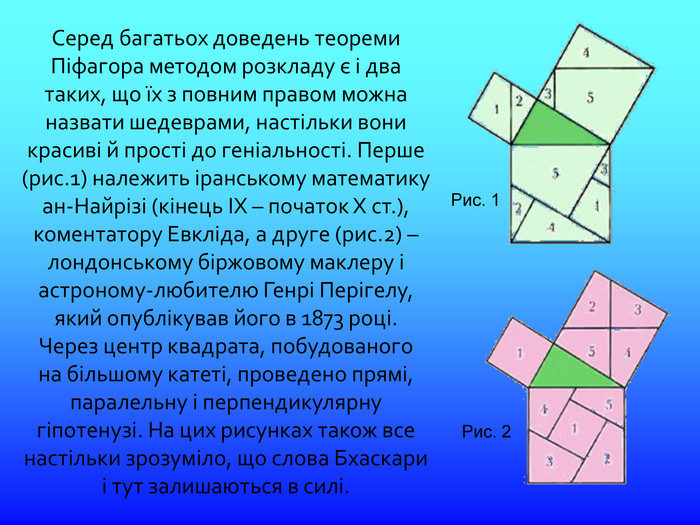
Рис. 1 Рис. 2 Серед багатьох доведень теореми Піфагора методом розкладу є і два таких, що їх з повним правом можна назвати шедеврами, настільки вони красиві й прості до геніальності. Перше (рис.1) належить іранському математику ан-Найрізі (кінець IX – початок Х ст.), коментатору Евкліда, а друге (рис.2) – лондонському біржовому маклеру і астроному-любителю Генрі Перігелу, який опублікував його в 1873 році. Через центр квадрата, побудованого на більшому катеті, проведено прямі, паралельну і перпендикулярну гіпотенузі. На цих рисунках також все настільки зрозуміло, що слова Бхаскари і тут залишаються в силі.

Як стверджують всі античні автори, Піфагор перший дав повне доведення теореми, яка має його ім'я. На жаль, ми не знаємо, в чому воно полягало, тому, що стародавні математики і письменники про це мовчать, а від самого Піфагора і ранніх піфагорійців до нас не дійшло жодного письмового документа.

Теорема Піфагора – одна із самих головних теорем геометрії. З її допомогою можна вивести більшість теорем. Сама ж теорема Піфагора чудова тим, що вона проста, але не очевидна. Цей збіг двох суперечливих початків і придає їй особливу привабливу силу, робить її красивою. Але, крім того, теорема Піфагора має величезне практичне значення: вона застосовується в геометрії буквально на кожному кроці.

Старовинні задачі: ? Случися некоему человеку к стене лествицу прибрати, у стены же тоя высота есть 117 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать.

? 125 117 х Розв'язання: Цю задачу взято з першого підручника математики на Русі. Називається він «Арифметика», автор його Леонтій Пилипович Магніцький. 1252 = 1172 + х2 х2 = 1252 – 1172 х2 = (125 – 117)(125 + 117) х2 = 8 ∙ 242 = 8 ∙ 2 ∙ 121 х = 4 ∙ 11 х = 44 (стопи) – від стіни.

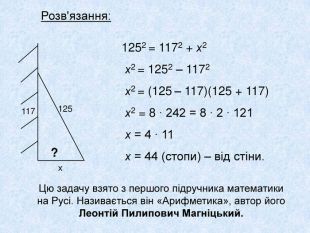
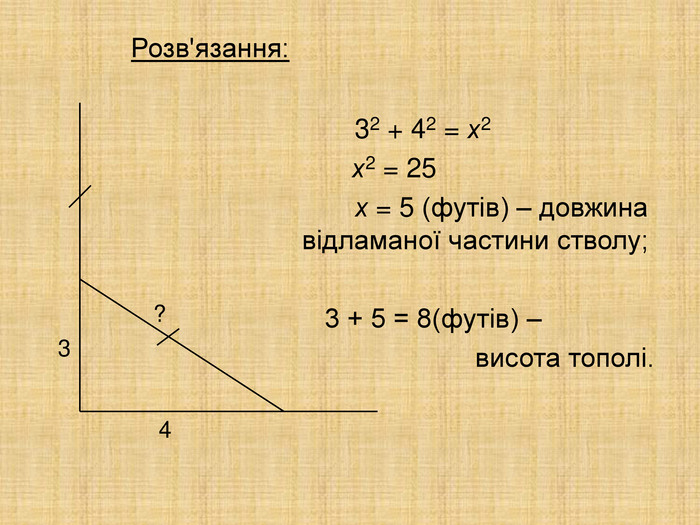
Часто математики записували свої задачі у віршованій формі. Ось одна із задач індійського математика XII ст. Бхаскари: 2. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в том месте река В четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?

Розв'язання: 4 3 ? 32 + 42 = х2 х2 = 25 х = 5 (футів) – довжина відламаної частини стволу; 3 + 5 = 8(футів) – висота тополі.

3. Є водойма зі стороною в один чжан = 10 чи. У центрі її росте очерет, який виступає над водою на 1 чи. Якщо потягнути очерет до берега, то він як раз торкнеться його. Питається: яка глибина води і яка довжина очерету? Задача з китайської “Математики в дев'яти книгах” з ілюстраціями

Розв'язання: Х 5 Х + 1 (х + 1)2 – х2 = 52 х2 + 2х + 1 – х2 = 25 2х = 24 х = 12(чи) = 1чжан 2 чи – глибина водойми; 12+1=13(чи)=1чжан 3 чи – довжина очерету.

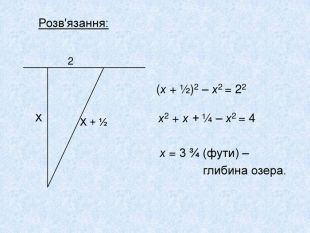
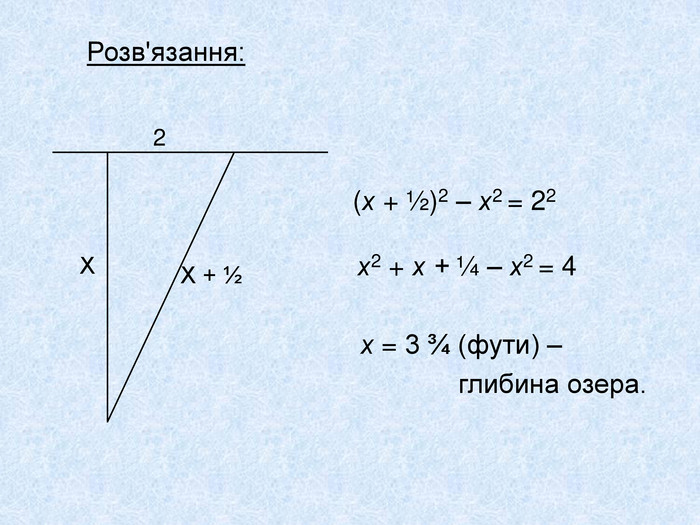
4. Над озером тихим, С полфута размером высился лотоса цвет. Он рос одиноко. И ветер порывом Отнес его в сторону. Нет Боле цветка над водой. Нашел же рыбак его ранней весной В двух футах от места, где рос. Итак, предложу я вопрос: Как озера вода здесь глубока? Ще одна задача стародавніх індусів також запропонована у віршах:

Розв'язання: Х 2 Х + Ѕ (х + Ѕ)2 – х2 = 22 х2 + х + ј – х2 = 4 х = 3 ѕ (фути) – глибина озера.

Піфагор – давньогрецький вчений (VI ст. до н.е.) Знаменитий грецький філософ і математик Піфагор Самоський, ім'ям якого названа теорема, жив у 580 - 500 рр. до н.ст. Біографічні відомості, які дійшли до нас про Піфагора уривчасті і далеко недостовірні. З його ім'ям пов'язано багато легенд.

Відомо, що Піфагор багато подорожував по країнам Сходу, відвідував Єгипет, Індію і Вавилон, вивчав стародавню культуру і досягнення науки різних країн. Коли повернувся, заснував гурток молоді з представників аристократії, яких приймали з великими церемоніями після довгих випробувань. Кожен вступаючий відрікався від свого майна і давав клятву зберігати у таємниці вчення засновника. Піфагорійська школа

Так на півдні Італії, яка була в ті часи грецькою колонією, виникла знаменита «Піфагорійська школа», яка зіграла важливу роль у науковому і політичному житті стародавньої Греції. Піфагорійці займалися математикою, філософією, природничими науками. Ними було зроблено багато важливих відкриттів в арифметиці і геометрії. Однак, у школі існував Декрет, по якому авторство всіх математичних робіт приписувалось Піфагору. Рафаель. Піфагор з учнями

Саме Піфагору приписують і доведення відомої геометричної теореми. На основі переказів видатних математиків (Прокл, Плутарх та др.), довгий час вважали, що до Піфагора ця теорема не була відома, звідси і назва – теорема Піфагора. Піфагор був убитий на вулиці під час народного повстання. Після його смерті учні оточили таємницею ім'я свого вчителя, так що з'ясувати правду про Піфагора неможливо.

До теореми Піфагора його учні складали віршики: «Піфагорові штани у всі боки рівні» А також малювали такі карикатури: Шарж з підручника XVI ст.

Теорему називали «мостом віслюків», так як слабкі учні, заучували теорему напам'ять, без розуміння, і прозвані тому «віслюками», були не в змозі подолати теорему Піфагора, яка була для них начебто неподоланного мосту. Або «втеча убогих», так як деякі «убогі» учні, які не мали серйозної математичної підготовки, «втікали» від геометрії.

В деяких списках «Початків» Евкліда теорема Піфагора називалася теоремою Німфи, «теорема – метелик», мабуть тому, що креслення схожі з метеликом, оскільки, словом «німфа» греки називали метелика. Німфами греки називали ще й наречених, а також деяких богинь. При перекладі з грецької арабський перекладач, напевно, не звернув уваги на креслення і переклав слово «німфа» не як «метелик», а як «наречена». Так і з'явилась ласкава назва знаменитої теореми – «Теорема Нареченої». «Німфа» - метелик, наречена

З давнини математики знаходять все нові і нові доведення теореми Піфагора. Таких доведень – більше або менше строгих, більше або менше наглядних – відомо коло півтори сотні (з інших джерел, більше п'ятисот), але бажання до збільшення їх числа збереглося. Тому теорема Піфагора занесена до «Книги рекордів Гіннеса». Самостійне «відкриття» доведення теореми Піфагора буде корисне і сучасним учням.

Послання іншим світам також відсилається у вигляді теореми Піфагора