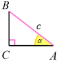
Конспект теми "Прямокутний трикутник".
ГЕОМЕТРІЯ, 8 ТЕМА 3. РОЗВ’ЯЗУВАННЯ ПРЯМОКУТНИХ ТРИКУТНИКІВ
Синус, косинус, тангенс і котангенс гострого кута прямокутного трикутника
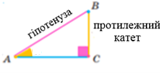


Означення. sinA = ![]() cosA =
cosA =![]() tgA =
tgA = ![]() ctgA =
ctgA = ![]()
 Теорема Піфагора
Теорема Піфагора
У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
Доведення.
 З вершини прямого кута трикутника ABC проведемо висоту CD. Доведемо, що AB2 = AC2 + BC2.
З вершини прямого кута трикутника ABC проведемо висоту CD. Доведемо, що AB2 = AC2 + BC2.
За теоремою про середні пропорційні відрізки у прямокутному трикутнику ABC маємо: AC2 = AB AD, BC2 = AB BD.
Додаємо дві рівності почленно: AC2 + BC2 = ABAD + AB BD = AB (AD + BD) = AB2. Отже, AB2 = AC2 + BC2![]()
Запам’ятай!



 Теорема, обернена до теореми Піфагора
Теорема, обернена до теореми Піфагора
Якщо в трикутнику квадрат однієї сторони дорівнює сумі квадратів двох інших сторін, то найбільший кут трикутника прямий.
 Перпендикуляр і похила
Перпендикуляр і похила


Властивості похилої
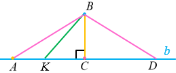
Будь-яка похила більша за перпендикуляр і за проєкцію цієї похилої.
 Рівні похилі мають рівні проєкції.
Рівні похилі мають рівні проєкції.
Із двох похилих більша та, у якої більша проєкція.
Розв’язати прямокутний трикутник – це означає знайти невідомі елементи трикутника (гіпотенузу, катети, гострі кути) за двома відомими елементами.
|
Розв’язування |
Співвідношення між сторонами і кутами прямокутних трикутників |
|
BC = c sin , АC = c cos . |
Катет дорівнює добутку гіпотенузи на синус протилежного кута Катет дорівнює добутку гіпотенузи на косинус прилеглого кута |
|
AB =
АC = |
Гіпотенуза дорівнює частці від ділення катета на синус протилежного кута Катет дорівнює частці від ділення другого катета на тангенс прилеглого кута |
|
B = 90 - A,
АC = |
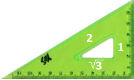
Значення синуса, косинуса, тангенса деяких кутів
tg45° = 1, sin60° = cos30° =
tg60° = |
|
tg А = B = 90 - A. |

про публікацію авторської розробки
Додати розробку