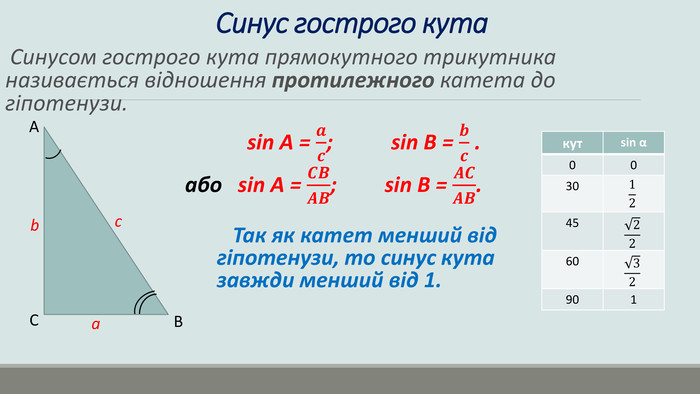
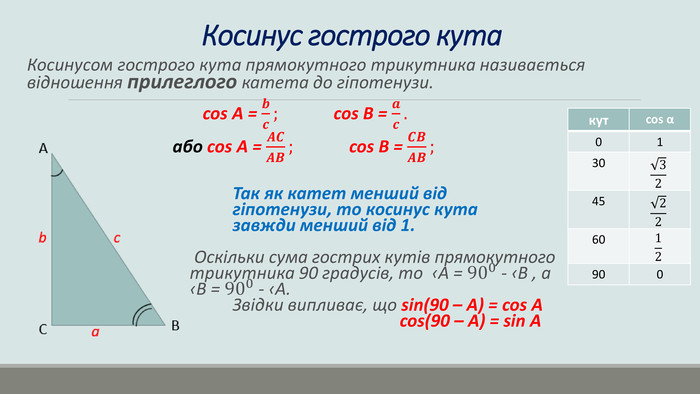
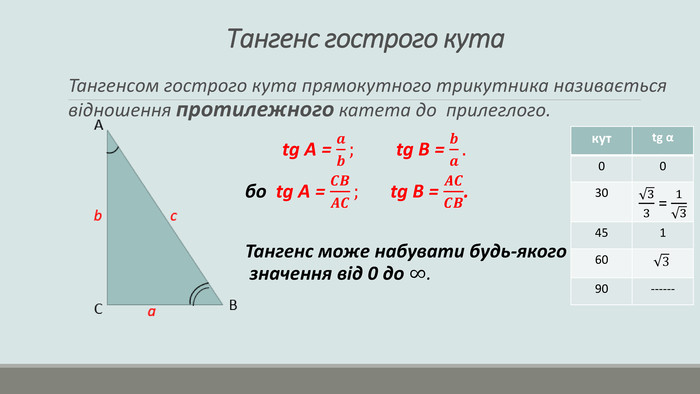
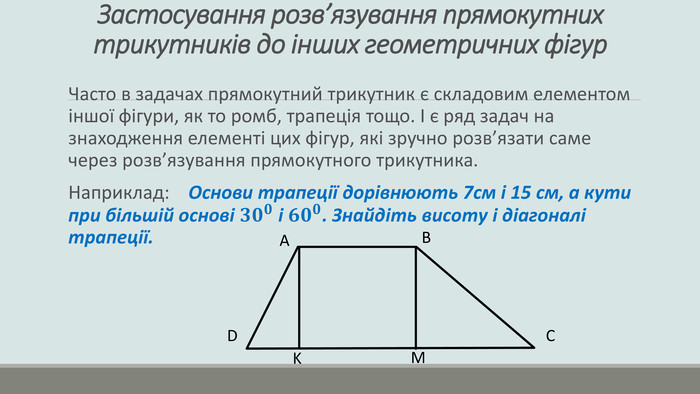
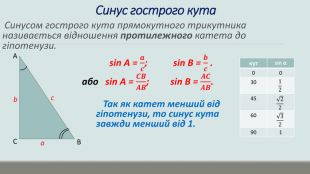
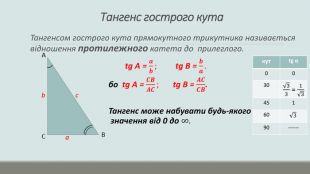
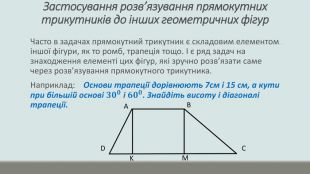
Презентація "Розв'язування прямокутних трикутників"
Про матеріал
Презентація призначена як для вивчення нового матеріалу, так і для закріплення перед контрольною роботою. Не містить посилання на певний підручник. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку