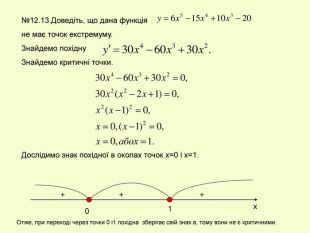
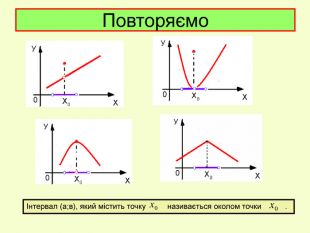
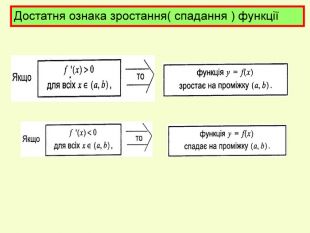
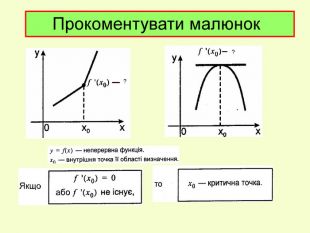
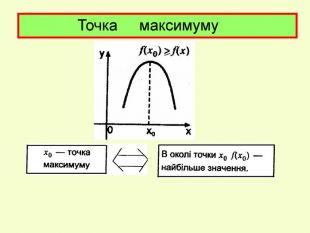
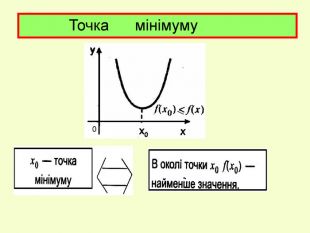
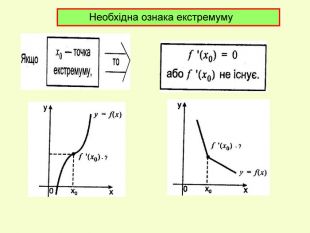
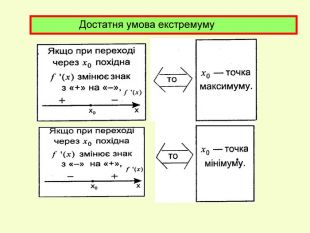
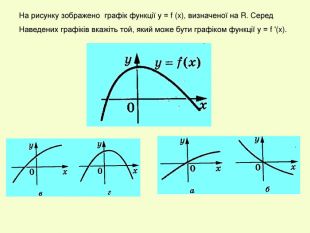
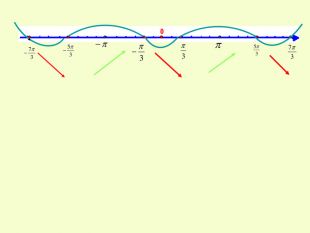
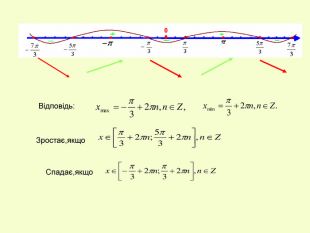
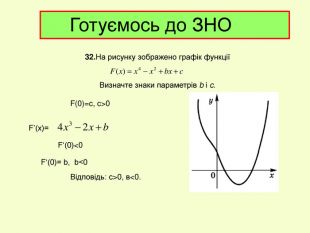
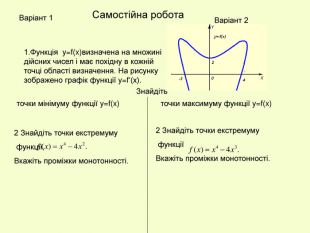
Презентація до уроку з алгебри в 11кл.Екстремуми функції.Необхідна і достатня умова екстремуму.
Про матеріал
Презентація до уроку з алгебри в 11кл.Екстремуми функції.Необхідна і достатня умова екстремуму.
--------------------------------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------------------------------
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дякую! Стисло і наочно!
-
ppt
До підручника
Алгебра (академічний, профільний рівень) 11 клас (Нелін Є.П., Долгова О.Є.)
До уроку
5.1. Застосування похідної до знаходження проміжків зростання і спадання та екстремумів функції Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





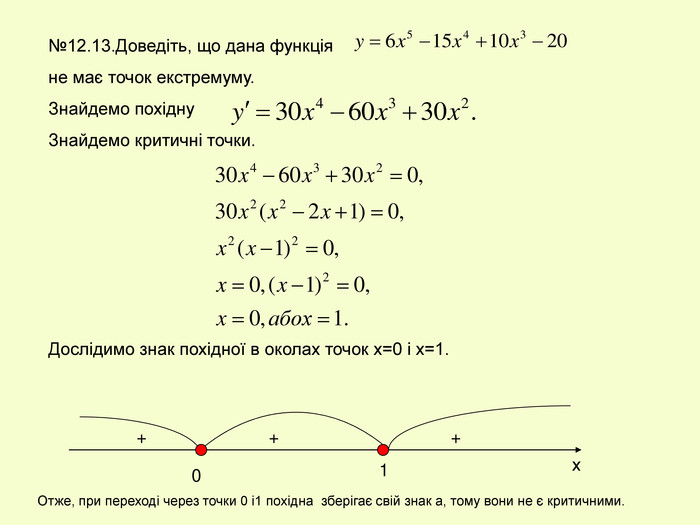
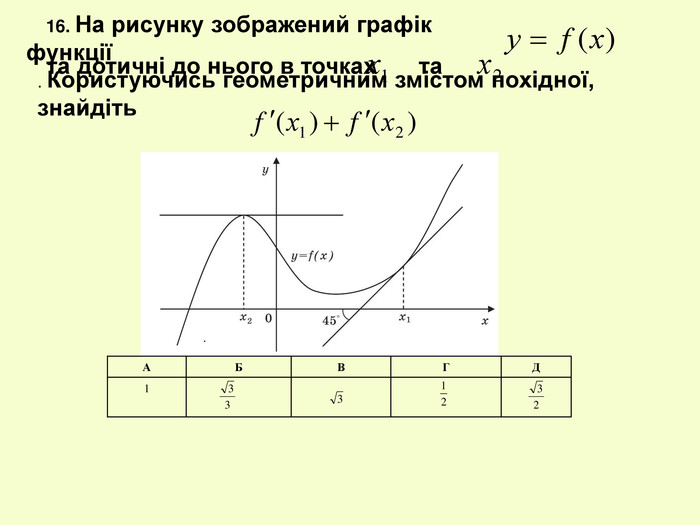
![12.15(1)Знайдіть проміжки зростання і спадання та точки екстремуму функції 1.Знайдемо D(f):х+2 0, х -2. 2.Знайдемо похідну 3.В точці х = -2 функція недиференційована. 4.Знайдемо критичні точки: (х+6)(х-2)=0,х = -6,х = 2. 5.Зясуємо знак похідної в околах критичних точок х = -6 і х = 2. -6 2 + + _ Зростає, якщо хЄ (- ; -6] U [2; ) Спадає, якщо х Є [-6;2] 12.15(1)Знайдіть проміжки зростання і спадання та точки екстремуму функції 1.Знайдемо D(f):х+2 0, х -2. 2.Знайдемо похідну 3.В точці х = -2 функція недиференційована. 4.Знайдемо критичні точки: (х+6)(х-2)=0,х = -6,х = 2. 5.Зясуємо знак похідної в околах критичних точок х = -6 і х = 2. -6 2 + + _ Зростає, якщо хЄ (- ; -6] U [2; ) Спадає, якщо х Є [-6;2]](/uploads/files/23459/11727/11934_images/6.jpg)


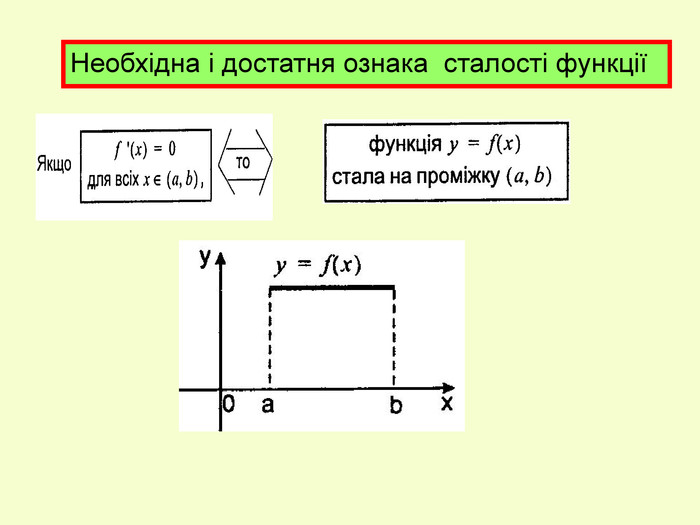
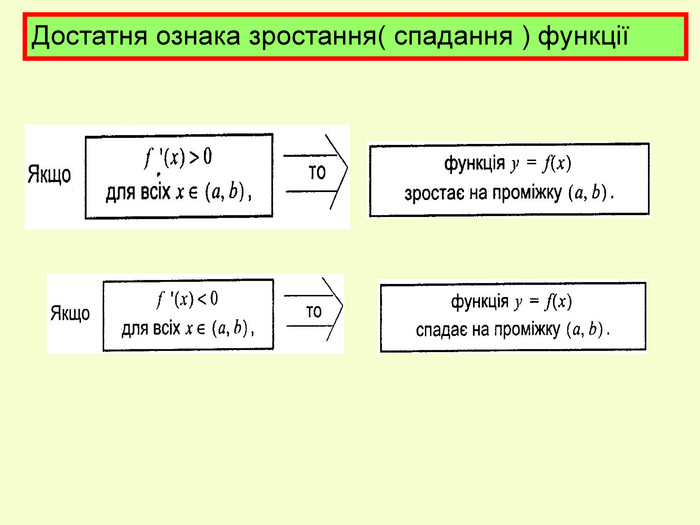
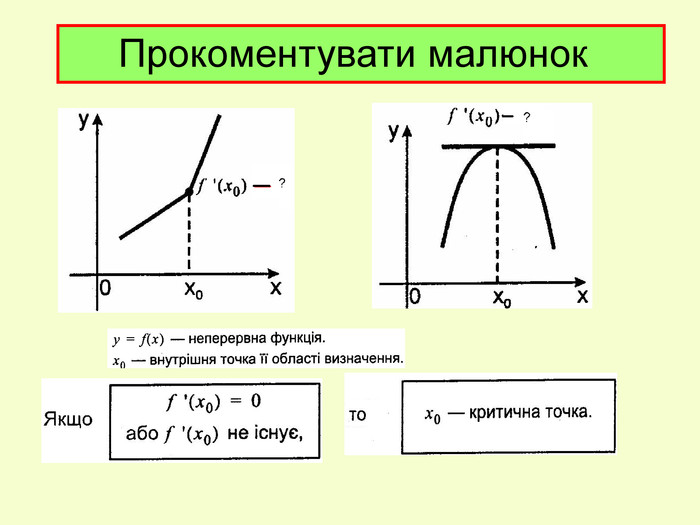





![Відповідь: №1. №1. Варіант 1 Варіант 2 Відповідь: D (f) = R D (f) = R №2 №2 + + - - 0 Відповідь: Зростає на проміжках [ ] і[ ] Спадає на проміжках [ ] і [ ] 0 3 - - + Відповідь: Зростає на проміжку [ 3; ] Спадає на проміжку [ ] Відповідь: №1. №1. Варіант 1 Варіант 2 Відповідь: D (f) = R D (f) = R №2 №2 + + - - 0 Відповідь: Зростає на проміжках [ ] і[ ] Спадає на проміжках [ ] і [ ] 0 3 - - + Відповідь: Зростає на проміжку [ 3; ] Спадає на проміжку [ ]](/uploads/files/23459/11727/11934_images/30.jpg)