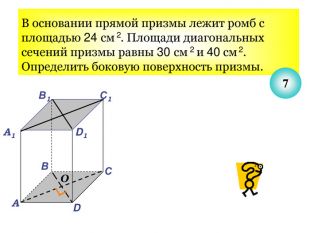
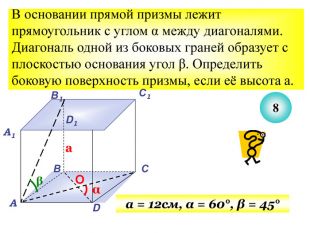
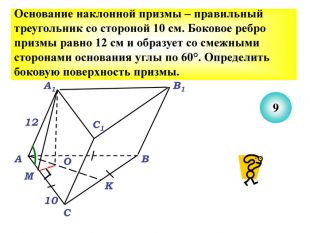
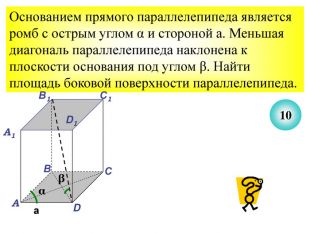
Презентація до уроку з теми: "Площа поверхні призми".
Про матеріал
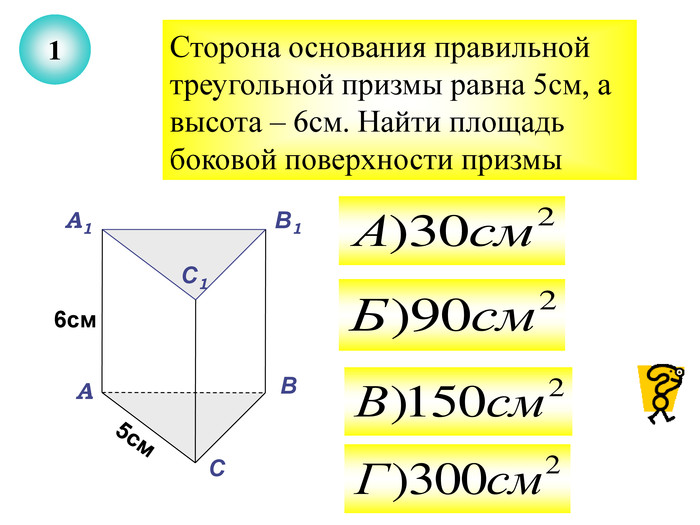
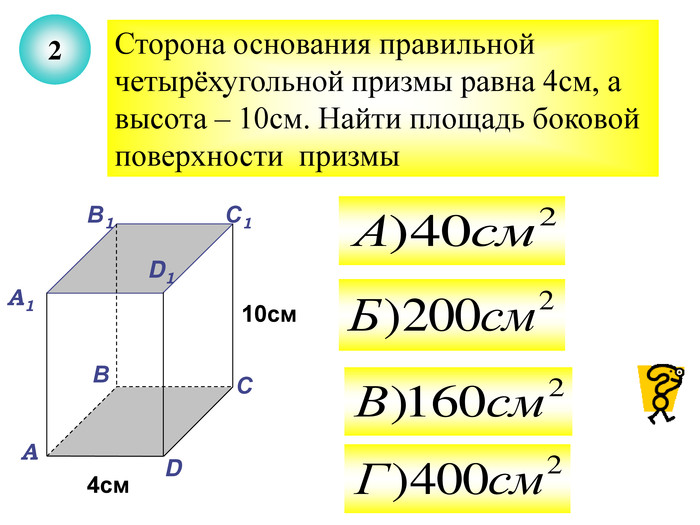
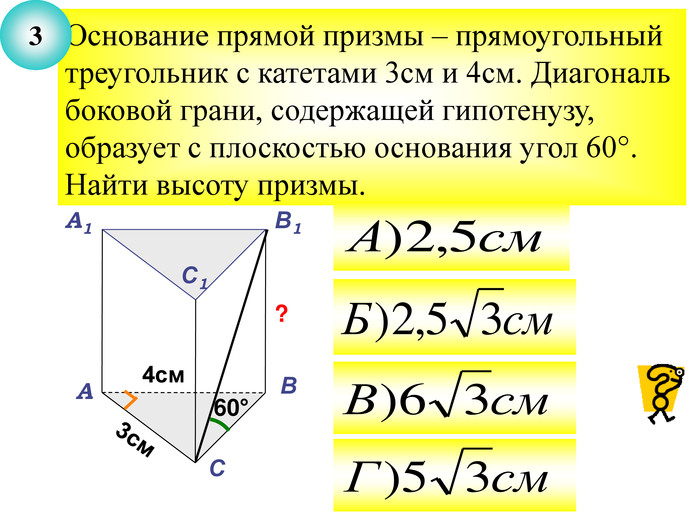
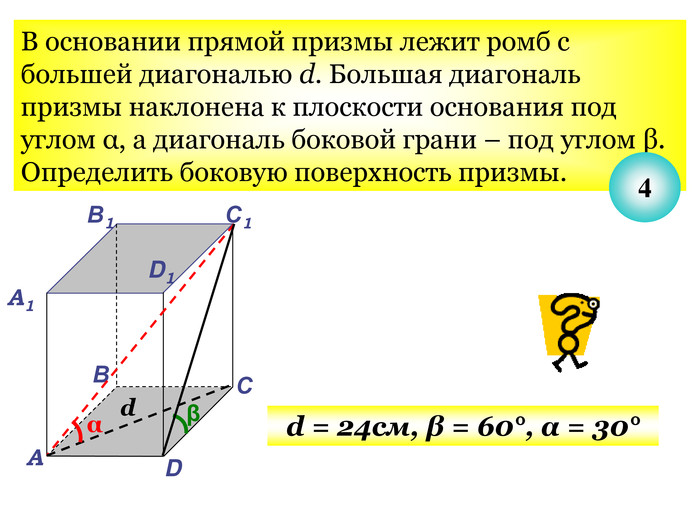
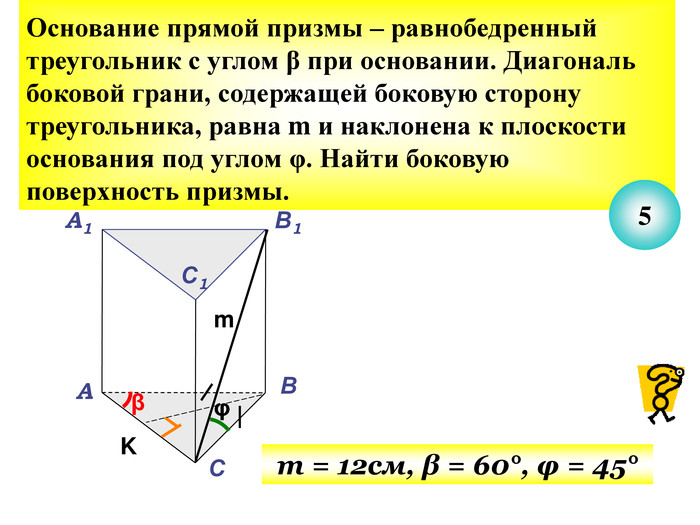
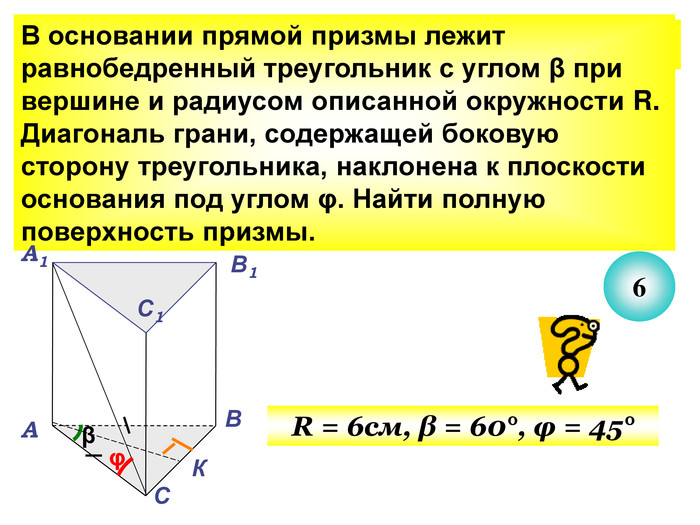
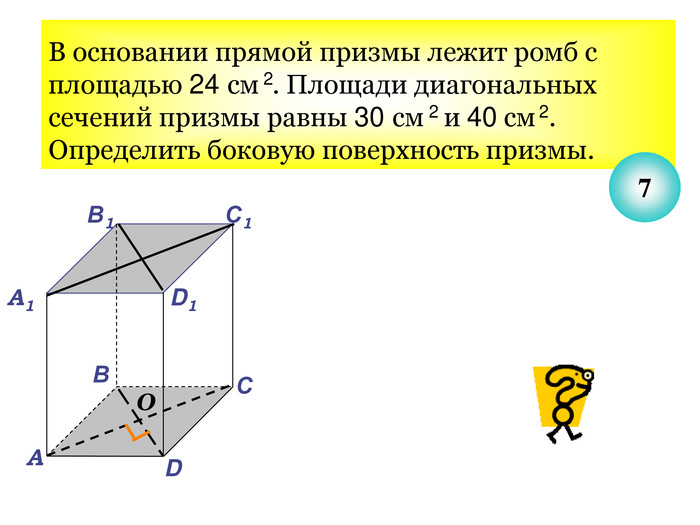
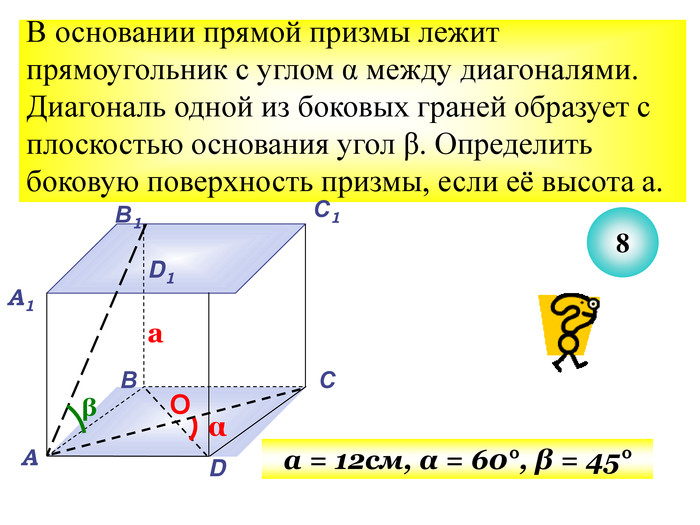
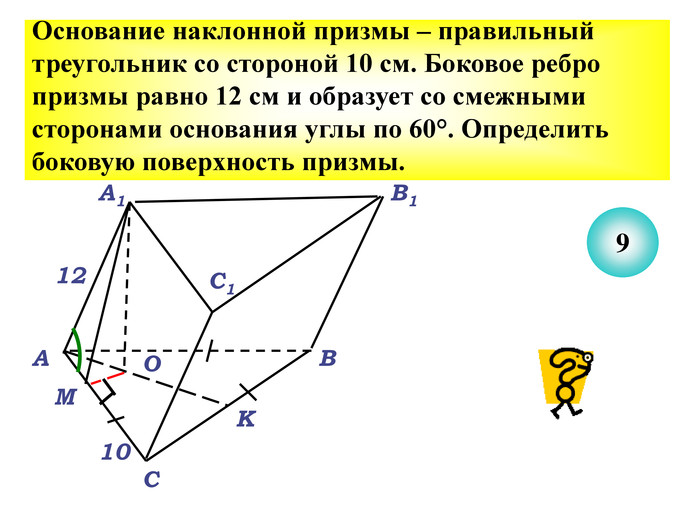
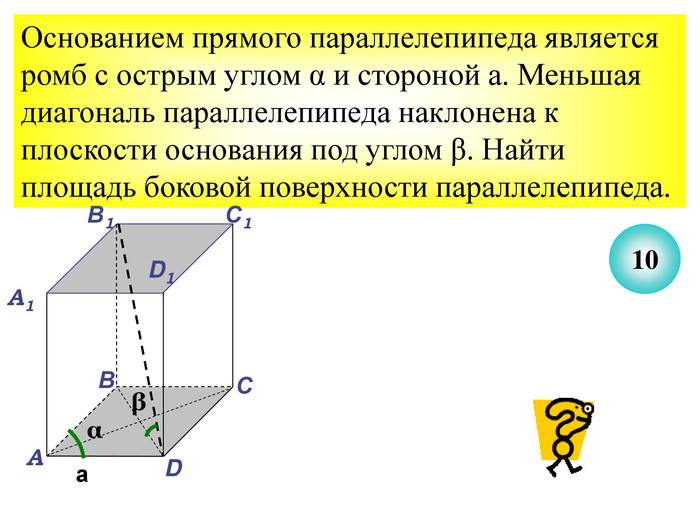
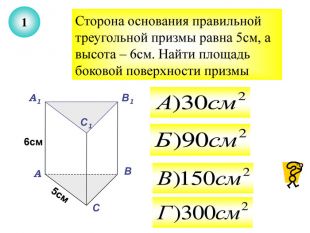
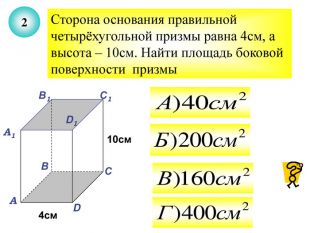
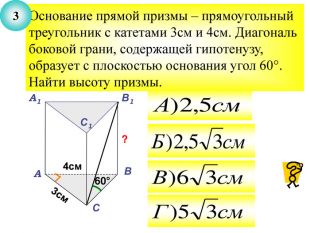
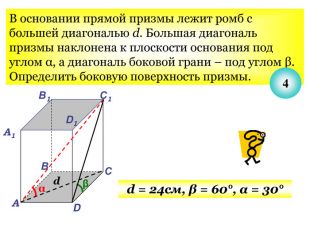
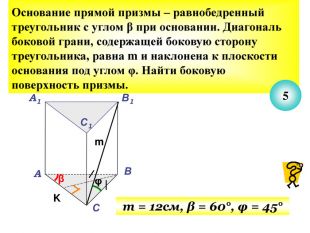
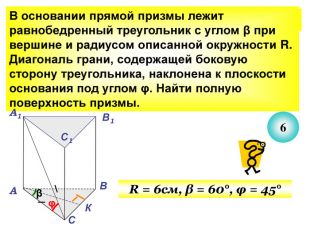
Презентація до уроку з теми "Площа поверхні призми" для 11 класу містить усні тестові задачі, та задачі з повним розв'язком по готовим малюнкам. Елементи малюнків з'являються поступово, по умові задачі.
Перегляд файлу
Зміст слайдів
ppt
До підручника
Геометрія (академічний, профільний рівень) 11 клас (Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку