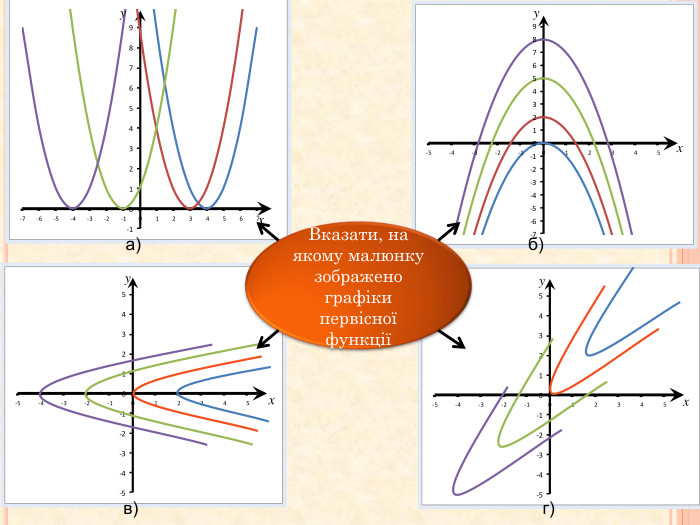
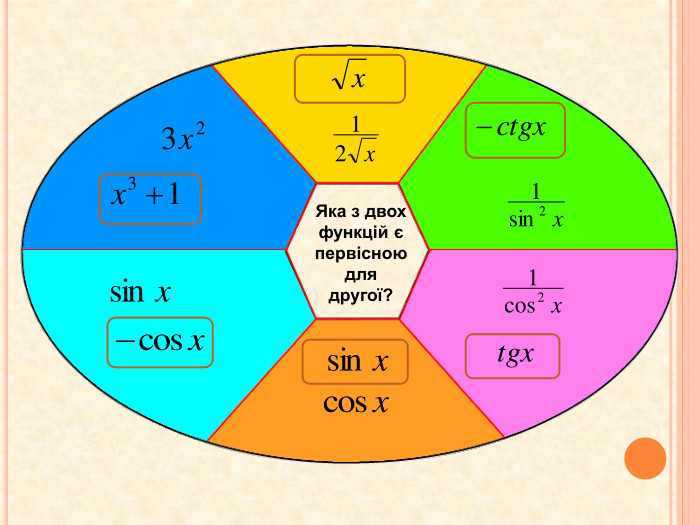
Презентація до відкритого уроку "Первісна. Правила знаходження первісних"
Про матеріал
Презантація відкритого уроку алгебрий в 11 класі. Матеріали презентації можна використовувати прт підготовці уроку алгебри по даній темі, так і при підготовці до відкритого уроку Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку