Презентація "Додавання і віднімання векторів"
Про матеріал
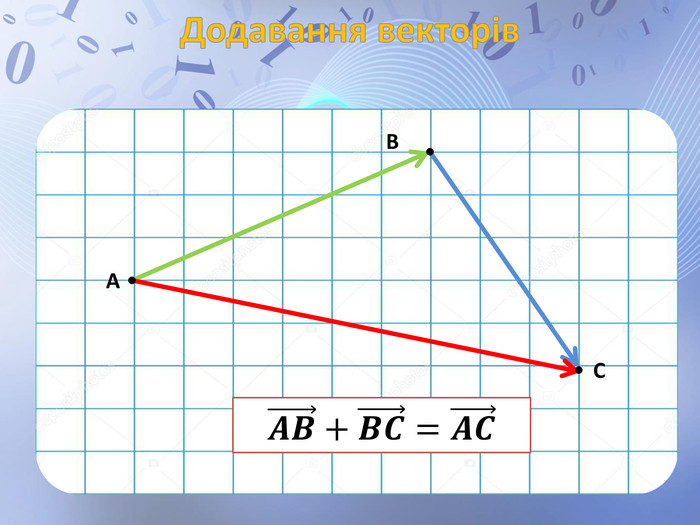
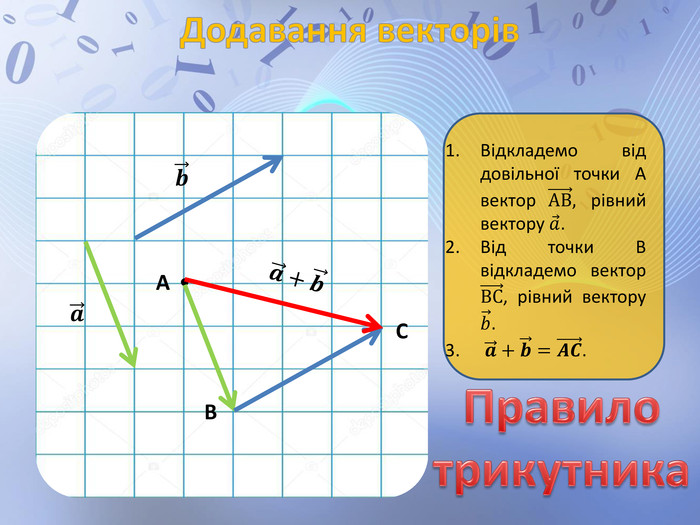
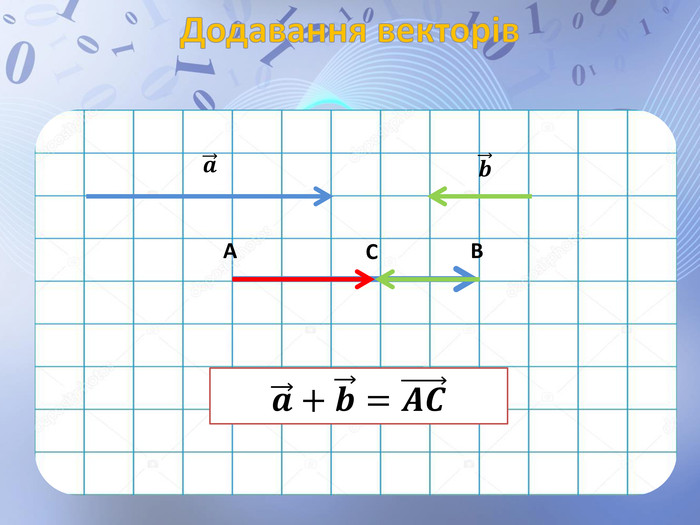
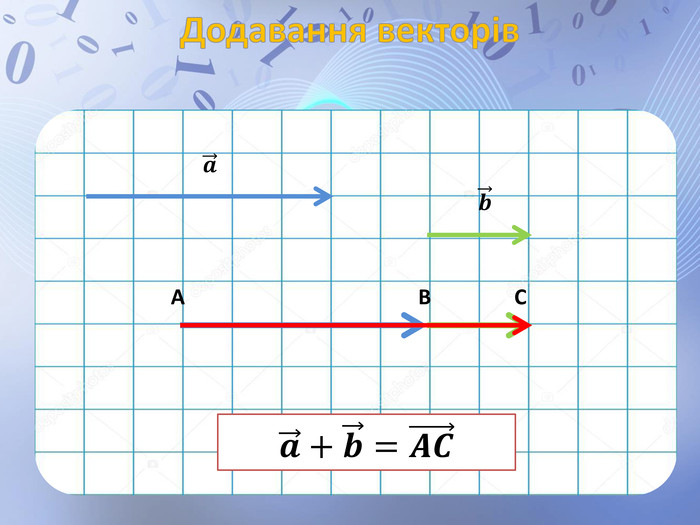
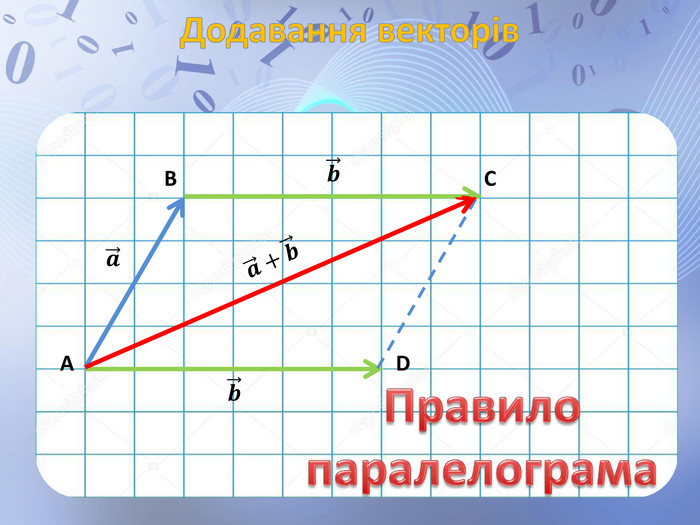
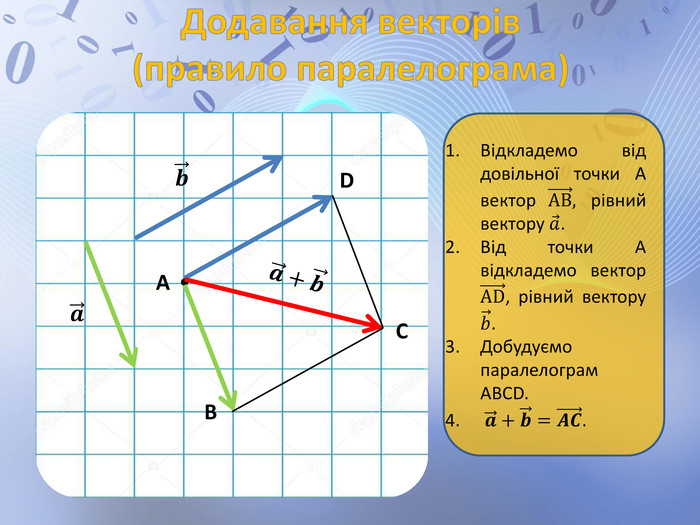
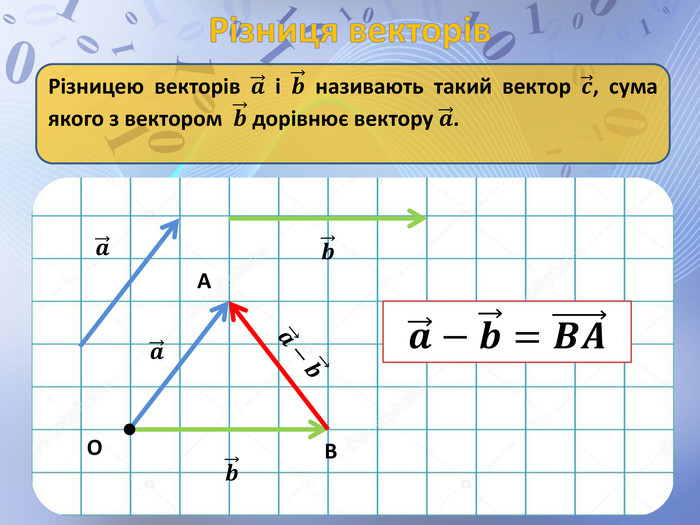
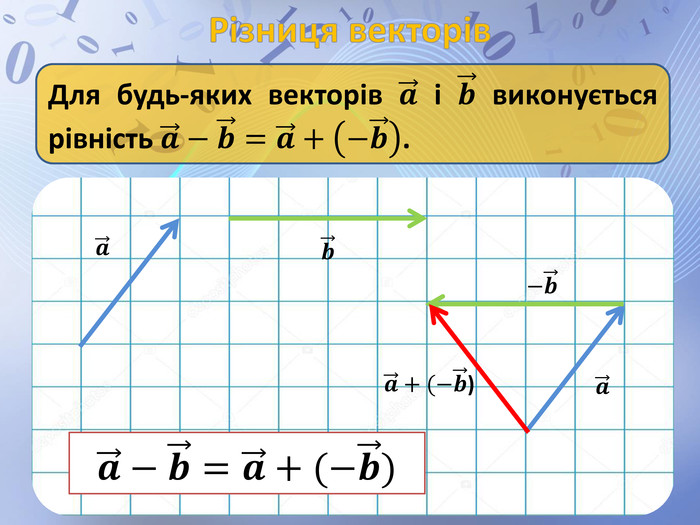
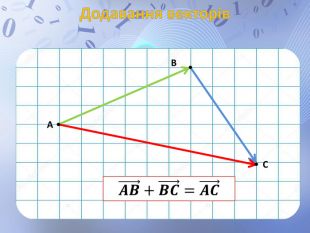
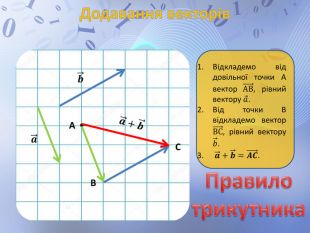
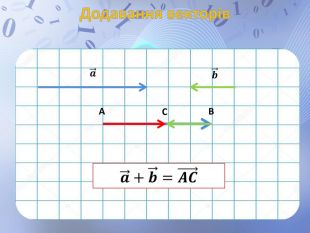
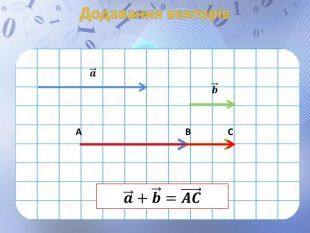
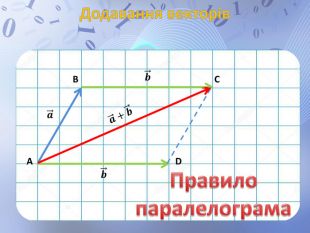
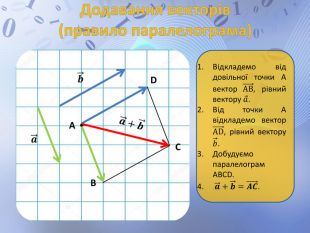
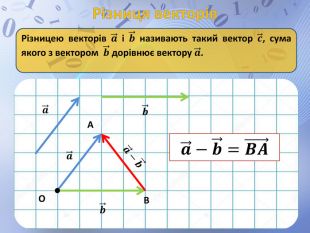
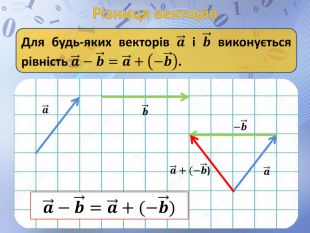
Презентація до уроку геометрії по темі "Додавання і віднімання векторів" містить анімовані ілюстрації до правил додавання векторів ( трикутника і паралелограма) і різниці векторів. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Геометрія 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку











-

Данилець Вікторія
27.01.2025 в 20:50
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вигоднер Діана Ісаківна
15.02.2024 в 00:05
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Бабійчук Валентина Йосипівна
14.02.2024 в 19:27
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Андрейченко Тетяна Олексіївна
09.01.2024 в 09:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
17.11.2023 в 10:17
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
13.11.2023 в 18:59
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Овчар Олена Анатоліївна
08.11.2023 в 11:11
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Крутько Світлана Олексіївна
25.10.2023 в 19:12
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Михайлівна Олена
03.06.2023 в 18:30
Загальна:
4.3
Структурованість
5.0
Оригінальність викладу
3.0
Відповідність темі
5.0
-

Вінник Валентина
02.11.2022 в 08:17
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Прохорчук Тетяна Павлівна
02.11.2021 в 20:55
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кушина Антоніна Василівна
21.10.2021 в 21:39
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Федишин Галина
20.02.2021 в 09:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Артеменко Наталія Ростиславівна
10.02.2021 в 05:39
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Распітін Світлана Володимирівна
24.11.2020 в 15:38
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горик Руслана Миколаївна
19.11.2020 в 02:06
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кучманюк Наталія Володимирівна
24.01.2020 в 11:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 14 відгуків