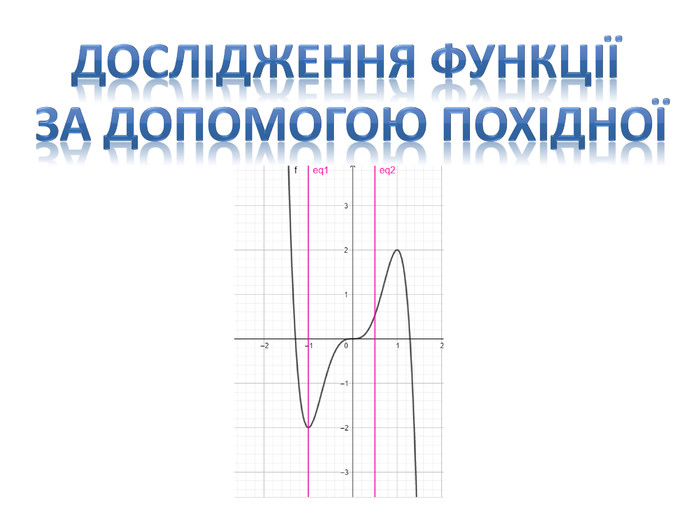
Презентація "Дослідження функції за допомогою похідної. Найбільше та найменше значення функції на відрізку"

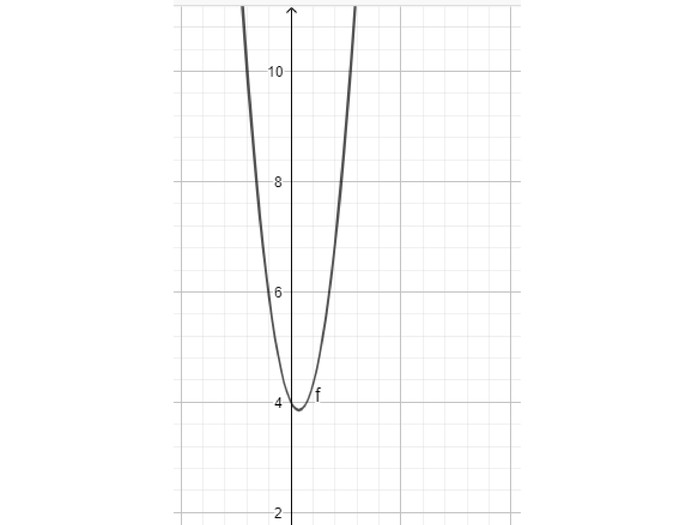
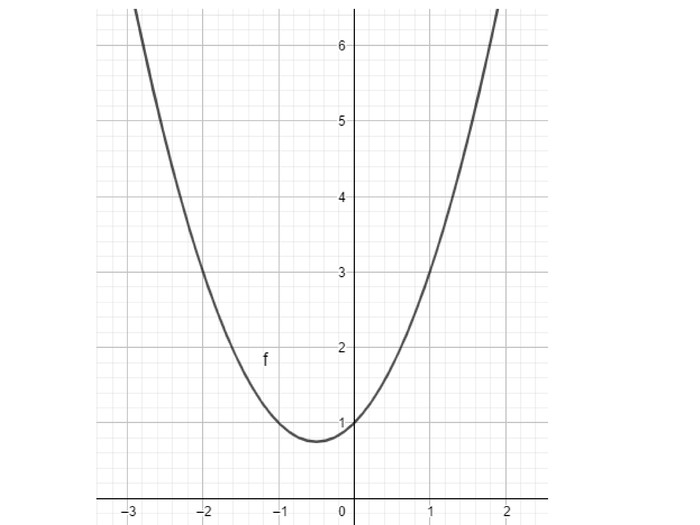
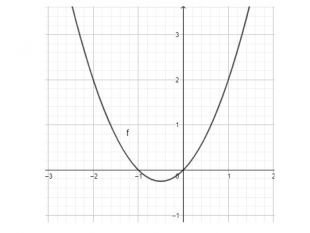
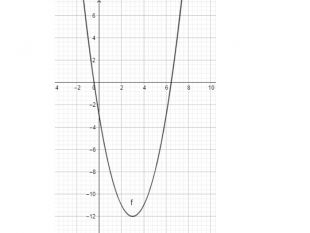
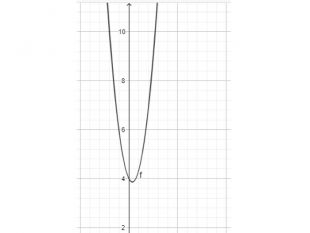
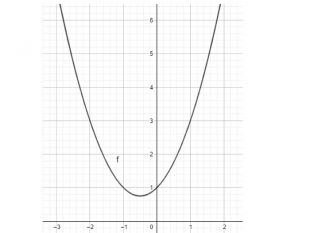
Дослідження функції за допомогою похідної

Геометричний зміст похідноїЗначення похідної функції y=f(x) в точці x0 рівне кутовому коефіцієнту (тангенсу кута нахилу) дотичної, проведеної до графіка функції в точці з абсцисою x0

Якщо похідна функції в кожній точці деякого проміжку додатня, то функція на ньому зростає. Якщо похідна функції в кожній точці деякого проміжку від’ємна, то функція на ньому спадає. Якщо похідна функції в кожній точці деякого проміжку дорівнює нулю, то функція на ньому є сталою.

Як визначити проміжки монотонності?Знайти похідну функціїЗнайти критичні точки функції (прирівняти похідну до нуля)Відмітити точки на координатній прямій. Встановити знаки похідної на утворених проміжках

Знайти похідну функції𝑓/𝑥=1+2𝑥 Знайти критичні точки функції (прирівняти похідну до нуля)1+2𝑥=0 𝑥=−12 Відмітити точки на координатній прямій−12 

Знайти похідну функції𝑓/𝑥=2𝑥−6 Знайти критичні точки функції (прирівняти похідну до нуля)2𝑥−6=0 𝑥=3 Відмітити точки на координатній прямій3

𝑓/𝑥=7∙2𝑥−2=14𝑥−2 14𝑥−2=0 𝑥=17 17 𝑥𝑚𝑖𝑛=17 𝑦𝑚𝑖𝑛=7∙172−2∙17+4=17−27+4=−17+4=367 

𝑓/𝑥=2𝑥+1 2𝑥+1=0 𝑥=−12 −12 𝑥𝑚𝑖𝑛=−12 𝑦𝑚𝑖𝑛=122+12+1=14+12+1=134 

Найбільше та найменше значення функції на відрізку

𝑓/𝑥=5∙3𝑥2−3∙5𝑥4=15𝑥2−15𝑥4 15𝑥2−15𝑥4=0 15𝑥21−𝑥2=0 𝑥=0 𝑥=1        𝑥=−1 Обираємо лише ті критичні точки, які належать вказаному відрізку𝑓0=5∙03−3∙05=0 𝑓1=5∙13−3∙15=2 𝑓−1=5∙−13−3∙−15=−2 𝑓−2=5∙−23−3∙−25=56 𝑓1=5∙23−3∙25=−56