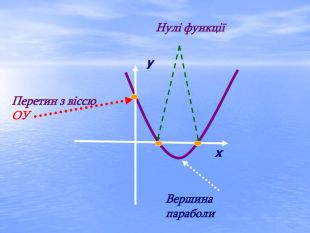
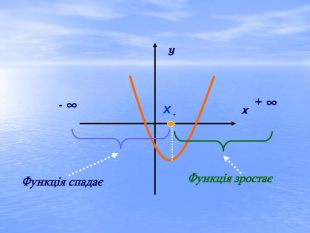
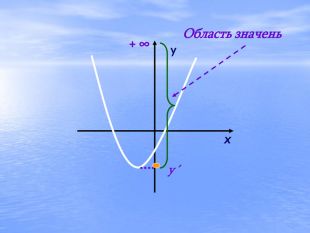
Презентація "Дослідження квадратичної функції" (9 клас)
Про матеріал
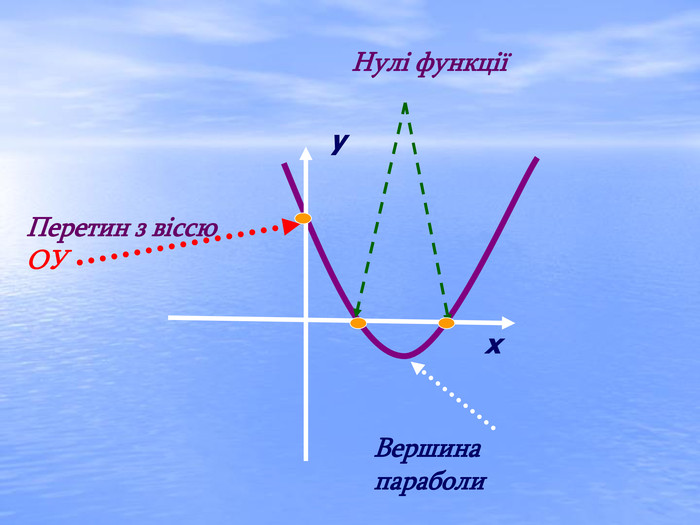
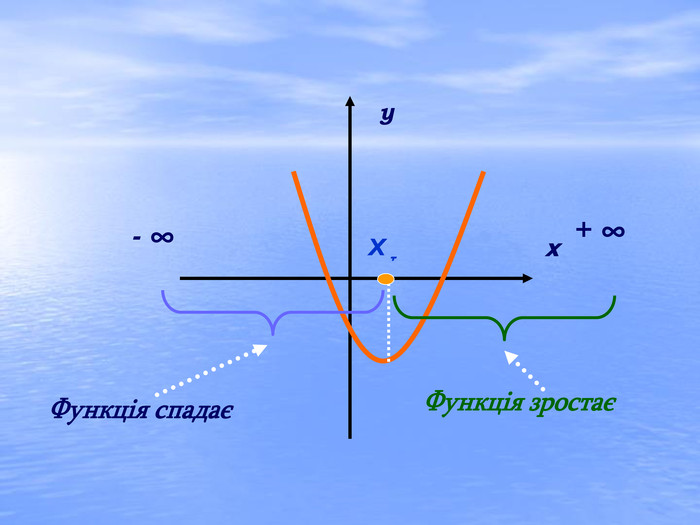
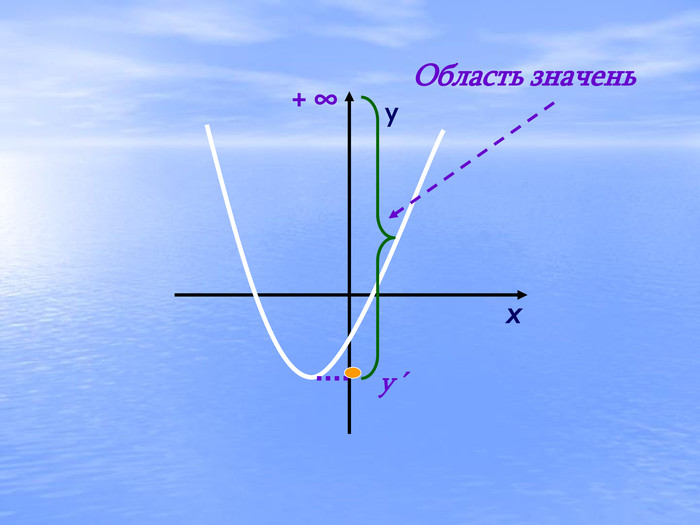
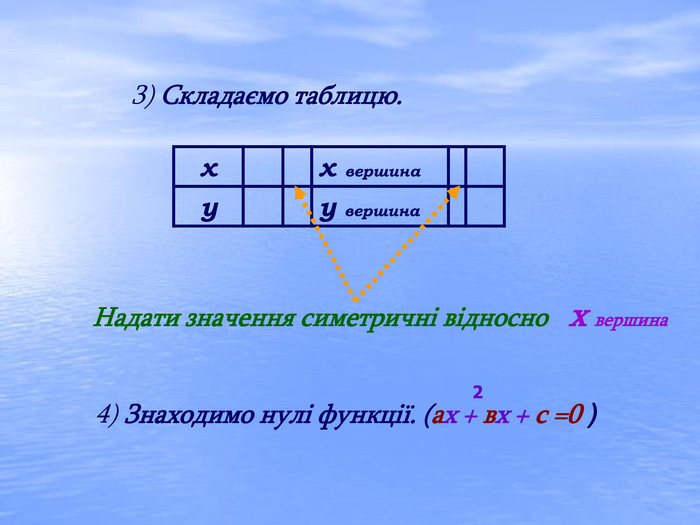
В презентації "Дослідження квадратичної функції" подані матеріали історичного характеру, практичного застосування функції та завдання, які можна використовувати для самостійної роботи, роботи в парах або ж в групах при закріпленні вивченого матеріалу.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
8. Властивості функції Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку