•Добуток кількості рядків на кількість стовпчиків m×n називають розміром матриці •Матрицю називають квадратною, якщо кількість рядків дорівнює кількості стовпчиків 

•Якщо кількість рядків не дорівнює кількості стовпчиків, матрицю називають

Якщо m=1, то матриця Якщо n=1, то матриця називається  називається   матрицею – рядком:       матрицею – cтовпцем: 

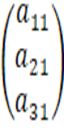
                  A=(a11a12….a1n                                          A=

Кількість рядків або стовпців квадратної матриці називають порядком матриці. 

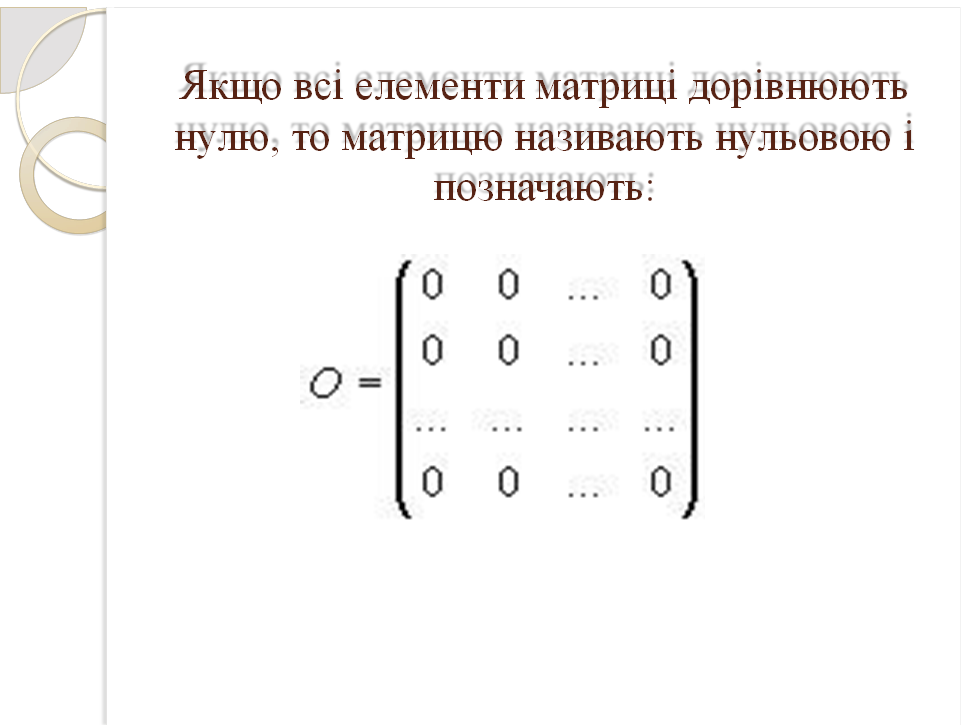
В квадратній матриці виділяють головну і побічну діагоналі.

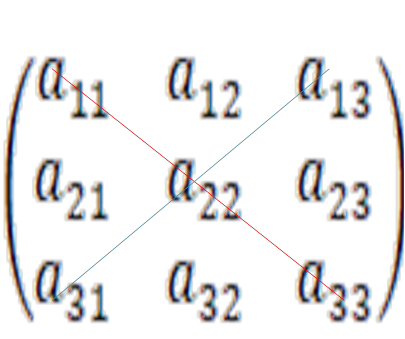
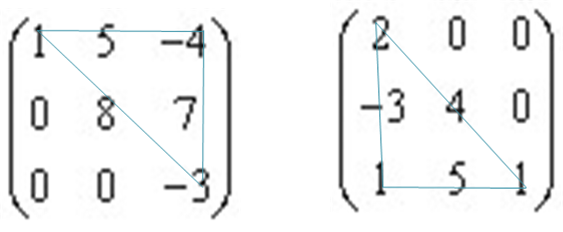
Квадратну матрицю називають трикутною, якщо всі елементи,

розташовані під (над) головною

діагоналлю, дорівнюють нулю, а серед тих, що залишилися є ненульові

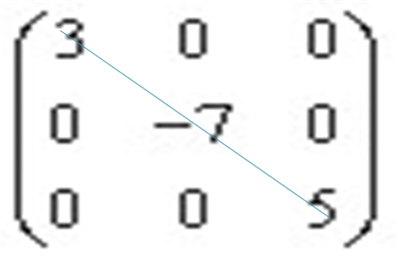
Квадратну матрицю, всі елементи якої, крім

елементів головної діагоналі, дорівнюють нулю, називають діагональною. 

Квадратну матрицю, всі елементи головної діагоналі якої дорівнюють одиниці, а всі інші нулю, називають одиничною і позначають

Матрицю А^T називають транспонованою  до матриці А, якщо її рядки є стовпчиками матриці А, а її стовпчики є рядками матриці А, тобто АT=((aij)m×n)т==(aji)n×m.

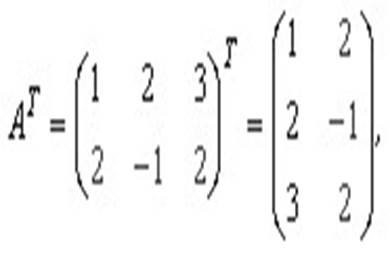
ДІЇ НАД МАТРИЦЯМИ

Нехай А та В матриці однакового розміру.

Сумою матриць А та В є матриця C=А+В того самого розміру, кожен елемент якої є сумою відповідних елементів матриць А та В

(cij=aij+bij).

Різницею матриць А та В називається матриця С=А-В, елементи якої дорівнюють різниці відповідних елементів матриць А та В 

(cij=aij-bij).

  Добутком довільного дійсного числа λ на 

  матрицю 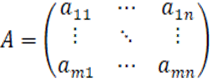  є матриця

Нехай А та В матриці, розмірів m×n та n×k відповідно

   Добутком матриці A_m×nна матрицю B_n×k називають таку матрицю C=A·B розміру m×k, у якої елемент c_ij є сумою добутків елементів i-го рядка матриці A на відповідні елементи j-го стовпчика матриці B:

                                            ,

     де i=1,2,….,m; j=1,2,….,n .

      a11 a12  Вираз Δ=  a₁₁ a₂₂  a₁₂ a₂₁ a21 a22

є визначником 2-го порядку

1 2

1423 2

3 4

Вираз                      a₁₁ a₁₂ a₁₃

Δ = a21 a22 a23 a11 a22 a33 a12 a23 a31 a13 a21 a32 a13 a22 a31 a11 a23 a32 a12 a33 a21 a31 a32 a33

є визначником 3-го порядку.

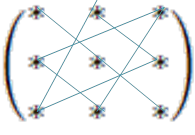Для обчислення визначника третього

                              порядку існує                     зі знаком

             правило трикутників                ^„+”  

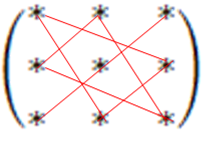
1 2 3зі знаком „–”  

4 5 61001206160

0 1 2

Властивості визначників 

1.                  Величина визначника не змінюється, якщо його рядки замінити стовпчиками, причому кожен рядок замінюють стовпчиком з тим же самим номером (тобто виконати транспонування елементів

визначника) 

2.                  Якщо у визначнику поміняти місцями лише два рядки (або два стовпчики), то визначник змінює знак на протилежний, зберігаючи абсолютне значення.

3.                  Якщо який-небудь з рядків (стовпців) визначника складається з нулів, то визначник дорівнює нулю.

4.                  Якщо визначник має два однакових стовпчика або два однакових рядка, то він дорівнює нулю.

5.                  Якщо визначник містить два пропорційних рядки (стовпчики), то значення його дорівнює нулю. 

Властивості визначників  

6.                              Якщо всі елементи деякого рядка (стовпчика) помножити на одне й те ж число, то значення визначника також помножиться на це число, то значення визначника також помножиться на це число. Звідси зрозуміло, що спільний множник всіх елементів рядка (стовпчика) можна винести за знак визначника.

7.                              Якщо кожний елемент деякого рядка (стовпчика) є сума двох доданків, то визначник можна представити у вигляді суми двох визначників: в першому з них на місці кожної суми лишається тільки перший доданок, а в другому – тільки другий доданок (інші елементи визначника зберігаються). 

8.                              Значення визначника не змінюється, якщо до елементів деякого рядка (стовпчика) додати відповідні елементи іншого паралельного рядка (стовпчика), помноживши їх попередньо на одне й те ж число.